19. (6分)计算:(1)$180^{\circ}-(75^{\circ}44^{\prime}8^{\prime\prime}+14^{\circ}15^{\prime}52^{\prime\prime})$;(2)$12^{\circ}15^{\prime}38^{\prime\prime}×2 + 62^{\circ}17^{\prime}÷3$.
答案:解:(1)原式=180°−89°59′60″=180°−90°=90°. (2)原式=24°30′76″+20°+(137÷3)′=44°30′76″+45′+120″÷3 =44°75′76″+40″=45°16′56″.
解析:
(1)解:原式=180°−(75°44′8″+14°15′52″)
=180°−89°59′60″
=180°−90°
=90°.
(2)解:原式=(12°×2+15′×2+38″×2)+(62°÷3+17′÷3)
=24°30′76″+20°+(137′÷3)
=24°30′76″+20°45′40″
=44°75′116″
=45°16′56″.
=180°−89°59′60″
=180°−90°
=90°.
(2)解:原式=(12°×2+15′×2+38″×2)+(62°÷3+17′÷3)
=24°30′76″+20°+(137′÷3)
=24°30′76″+20°45′40″
=44°75′116″
=45°16′56″.
20. (6分)尺规作图:如图,在平面内有A,B,C三点.
(1)画直线AB,射线AC,线段BC.
(2)在线段BC上任取一点D(不同于点B,C),连接AD,并延长AD至点E,使$DE = AD$.

(1)画直线AB,射线AC,线段BC.
(2)在线段BC上任取一点D(不同于点B,C),连接AD,并延长AD至点E,使$DE = AD$.

答案:
解:(1)如答图,直线AB,射线AC,线段BC即为所求. (2)如答图,线段AD,DE即为所求.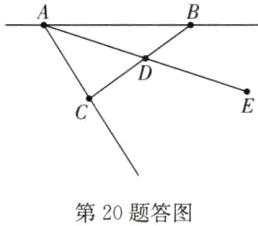
解:(1)如答图,直线AB,射线AC,线段BC即为所求. (2)如答图,线段AD,DE即为所求.

21. (8分)如图,$\angle AOB$是平角,OM,ON分别是$\angle AOC$,$\angle BOD$的平分线.
(1)若$\angle AOC = 40^{\circ}$,$\angle BOD = 60^{\circ}$,求$\angle MON$的度数.
(2)若只给条件“$\angle COD = 80^{\circ}$”,你能求出$\angle MON$的度数吗?如果能,请给出过程;如果不能,请说明理由.

(1)若$\angle AOC = 40^{\circ}$,$\angle BOD = 60^{\circ}$,求$\angle MON$的度数.
(2)若只给条件“$\angle COD = 80^{\circ}$”,你能求出$\angle MON$的度数吗?如果能,请给出过程;如果不能,请说明理由.

答案:解:(1)∵∠AOB是平角,∠AOC=40°,∠BOD=60°,∴∠COD=∠AOB−∠AOC−∠BOD=180°−40°−60°=80°.∵OM,ON分别是∠AOC,∠BOD的平分线,∴∠MOC=$\frac{1}{2}$∠AOC=20°,∠NOD=$\frac{1}{2}$∠BOD=30°.∴∠MON=∠MOC+∠COD+∠NOD=20°+80°+30°=130°. (2)能.过程如下:∵OM,ON分别是∠AOC,∠BOD的平分线,∴∠MOC+∠NOD=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOD=$\frac{1}{2}$(∠AOC+∠BOD)=$\frac{1}{2}$×(180°−80°)=50°.∴∠MON=∠MOC+∠NOD+∠COD=50°+80°=130°.
22. (8分)如图,已知$AB= \frac{1}{4}BM= \frac{1}{5}AN$,点C,D分别是BM,AN的中点,且$CD = 14$.
(1)求证:$BM = BN$;
(2)求MN的长.

(1)求证:$BM = BN$;
(2)求MN的长.

答案:(1)证明:因为AB=$\frac{1}{4}$BM=$\frac{1}{5}$AN,所以BM=4AB,AN=5AB,则BN=AN−AB=4AB,所以BM=BN. (2)解:设AB=x,则BM=4x,AN=5x,所以BN=4x,MN=BM+BN=8x.又因为C,D分别是BM,AN的中点,所以CD=BC+BD=BC+(AD−AB)=$\frac{1}{2}$BM+($\frac{1}{2}$AN−AB),所以2x+(2.5x−x)=14,解得x=4,则MN=8x=32.
解析:
(1)证明:因为$AB = \frac{1}{4}BM = \frac{1}{5}AN$,所以$BM = 4AB$,$AN = 5AB$,则$BN = AN - AB = 5AB - AB = 4AB$,所以$BM = BN$。
(2)解:设$AB = x$,则$BM = 4x$,$AN = 5x$,由(1)知$BN = 4x$,所以$MN = BM + BN = 4x + 4x = 8x$。因为点$C$,$D$分别是$BM$,$AN$的中点,所以$BC = \frac{1}{2}BM = 2x$,$AD = \frac{1}{2}AN = 2.5x$,则$BD = AD - AB = 2.5x - x = 1.5x$,所以$CD = BC + BD = 2x + 1.5x = 3.5x$。又因为$CD = 14$,所以$3.5x = 14$,解得$x = 4$,则$MN = 8x = 8×4 = 32$。
(2)解:设$AB = x$,则$BM = 4x$,$AN = 5x$,由(1)知$BN = 4x$,所以$MN = BM + BN = 4x + 4x = 8x$。因为点$C$,$D$分别是$BM$,$AN$的中点,所以$BC = \frac{1}{2}BM = 2x$,$AD = \frac{1}{2}AN = 2.5x$,则$BD = AD - AB = 2.5x - x = 1.5x$,所以$CD = BC + BD = 2x + 1.5x = 3.5x$。又因为$CD = 14$,所以$3.5x = 14$,解得$x = 4$,则$MN = 8x = 8×4 = 32$。