23. (14分)如图是一个长方体的展开图,一共标有A,B,C,D,E,F六个面,$MN = 2$,$NO = x$,$OP = y$,请根据要求回答：
(1)如果A面在长方体的底部,那么
(2)求这个长方体的表面积和体积；(用含x和y的式子表示)
(3)若$A = a^{3}+\frac{1}{2}a^{2}b + 3$,$B= \frac{1}{2}a^{2}b - 3$,$C = a^{3}-1$,$D = -\frac{1}{2}(a^{2}b - 6)$,且相对两个面上式子的和都相等,求E代表的代数式.
(1)如果A面在长方体的底部,那么
F
面会在上面；(2)求这个长方体的表面积和体积；(用含x和y的式子表示)
解:由题意可知，这个长方体的长为x,宽为y,高为2,因此表面积为(xy+2x+2y)×2=2xy+4x+4y,体积为2xy.
(3)若$A = a^{3}+\frac{1}{2}a^{2}b + 3$,$B= \frac{1}{2}a^{2}b - 3$,$C = a^{3}-1$,$D = -\frac{1}{2}(a^{2}b - 6)$,且相对两个面上式子的和都相等,求E代表的代数式.
解:由题意可知,B+D=C+E,所以E=B+D−C =($\frac{1}{2}$a²b−3)−$\frac{1}{2}$(a²b−6)−(a³−1)=$\frac{1}{2}$a²b−3−$\frac{1}{2}$a²b+3−a³+1 =1−a³,即E代表的代数式为1−a³.
答案：(1)F (2)解:由题意可知，这个长方体的长为x,宽为y,高为2,因此表面积为(xy+2x+2y)×2=2xy+4x+4y,体积为2xy. (3)解:由题意可知,B+D=C+E,所以E=B+D−C =($\frac{1}{2}$a²b−3)−$\frac{1}{2}$(a²b−6)−(a³−1)=$\frac{1}{2}$a²b−3−$\frac{1}{2}$a²b+3−a³+1 =1−a³,即E代表的代数式为1−a³.
解析：
(1)F
(2)解：由题意得，长方体的长为x，宽为y，高为2。
表面积：$(xy + 2x + 2y)×2 = 2xy + 4x + 4y$
体积：$x×y×2 = 2xy$
(3)解：由题意知相对面的和相等，A与F相对，B与D相对，C与E相对，所以$B + D = C + E$。
$E = B + D - C$
$= (\frac{1}{2}a^{2}b - 3) + [-\frac{1}{2}(a^{2}b - 6)] - (a^{3} - 1)$
$= \frac{1}{2}a^{2}b - 3 - \frac{1}{2}a^{2}b + 3 - a^{3} + 1$
$= 1 - a^{3}$
(2)解：由题意得，长方体的长为x，宽为y，高为2。
表面积：$(xy + 2x + 2y)×2 = 2xy + 4x + 4y$
体积：$x×y×2 = 2xy$
(3)解：由题意知相对面的和相等，A与F相对，B与D相对，C与E相对，所以$B + D = C + E$。
$E = B + D - C$
$= (\frac{1}{2}a^{2}b - 3) + [-\frac{1}{2}(a^{2}b - 6)] - (a^{3} - 1)$
$= \frac{1}{2}a^{2}b - 3 - \frac{1}{2}a^{2}b + 3 - a^{3} + 1$
$= 1 - a^{3}$
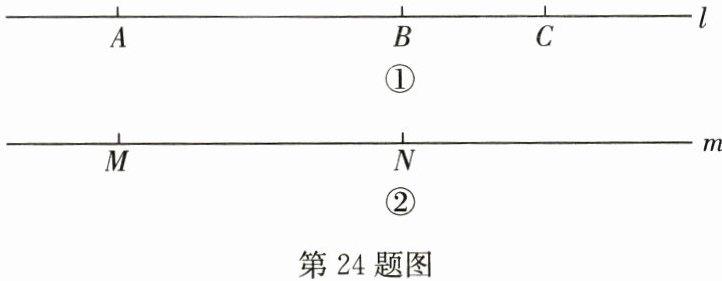
24. (14分)直线l上的三个点E,F,O,若满足$FO= \frac{1}{2}EF$,则称点O是点E关于点F的“半距点”.如图①,$BC= \frac{1}{2}AB$,此时点C就是点A关于点B的一个“半距点”.如图②,若M,N,P三个点在同一条直线m上,且点P是点M关于点N的“半距点”,$MN = 6cm$.
(1)求MP的长；
(2)若点G也是直线m上一点,且G是线段MP的中点,求线段GN的长.
(1)求MP的长；
(2)若点G也是直线m上一点,且G是线段MP的中点,求线段GN的长.
答案：
解:(1)∵点P是点M关于点N的“半距点”,∴PN=$\frac{1}{2}$MN.①如答图①,∵MN=6cm,点P₁是点M关于点N的“半距点”,∴P₁N=$\frac{1}{2}$MN=3(cm),∴MP₁=MN−P₁N=3(cm).②如答图②,∵MN=6cm,点P₂是点M关于点N的“半距点”,∴P₂N=$\frac{1}{2}$MN=3(cm),∴MP₂=MN+P₂N=9(cm).综上，MP的长为3cm或9cm. M G P₁ N m
(2)①如答图①,G₁是线段MP₁的中点,∴MG₁=$\frac{1}{2}$MP₁=$\frac{3}{2}$(cm),∴G₁N=MN−MG₁=6−$\frac{3}{2}$=$\frac{9}{2}$(cm).②如答图②,G₂是线段MP₂的中点,∴MG₂=$\frac{1}{2}$MP₂=$\frac{9}{2}$(cm),∴G₂N=MN−MG₂=6−$\frac{9}{2}$=$\frac{3}{2}$(cm).综上，线段GN的长为$\frac{9}{2}$cm或$\frac{3}{2}$cm.
解:(1)∵点P是点M关于点N的“半距点”,∴PN=$\frac{1}{2}$MN.①如答图①,∵MN=6cm,点P₁是点M关于点N的“半距点”,∴P₁N=$\frac{1}{2}$MN=3(cm),∴MP₁=MN−P₁N=3(cm).②如答图②,∵MN=6cm,点P₂是点M关于点N的“半距点”,∴P₂N=$\frac{1}{2}$MN=3(cm),∴MP₂=MN+P₂N=9(cm).综上，MP的长为3cm或9cm. M G P₁ N m
(2)①如答图①,G₁是线段MP₁的中点,∴MG₁=$\frac{1}{2}$MP₁=$\frac{3}{2}$(cm),∴G₁N=MN−MG₁=6−$\frac{3}{2}$=$\frac{9}{2}$(cm).②如答图②,G₂是线段MP₂的中点,∴MG₂=$\frac{1}{2}$MP₂=$\frac{9}{2}$(cm),∴G₂N=MN−MG₂=6−$\frac{9}{2}$=$\frac{3}{2}$(cm).综上，线段GN的长为$\frac{9}{2}$cm或$\frac{3}{2}$cm.