10.(12分)计算:
(1)$48^{\circ}39' + 67^{\circ}31'$; (2)$\frac{11}{5}×(-\frac{1}{3} - \frac{1}{2})×\frac{9}{11}÷(-\frac{3}{2})^{2}$.
(1)$48^{\circ}39' + 67^{\circ}31'$; (2)$\frac{11}{5}×(-\frac{1}{3} - \frac{1}{2})×\frac{9}{11}÷(-\frac{3}{2})^{2}$.
答案:解:(1)原式=115°70′=116°10′.
(2)原式=$\frac{11}{5}×(-\frac{5}{6})×\frac{9}{11}÷\frac{9}{4}=-\frac{3}{2}×\frac{4}{9}=-\frac{2}{3}$.
(2)原式=$\frac{11}{5}×(-\frac{5}{6})×\frac{9}{11}÷\frac{9}{4}=-\frac{3}{2}×\frac{4}{9}=-\frac{2}{3}$.
11.(10分)先化简,再求值:$2a^{2} - 5a + 2 - 6a^{2} + 6a - 3$,其中$a = -1$.
答案:解:原式=-4a²+a-1,
把a=-1代入得,
原式=-4×(-1)²+(-1)-1=-6.
把a=-1代入得,
原式=-4×(-1)²+(-1)-1=-6.
12.(14分)为了支持国货,某手机卖场本月计划用9万元购进某国产品牌手机,从卖场获知该品牌3种不同型号的手机进价及售价如下表:
|手机型号|A|B|C|
|进价/(元/部)|1500|2100|2500|
|售价/(元/部)|1650|2300|2750|
若该手机卖场同时购进两种不同型号的手机共50台,9万元刚好用完.
(1)请你确定该手机卖场的进货方案,并说明理由;
(2)该卖场老板准备把这批手机销售利润的50%捐给公益组织,在同时购进两种不同型号手机的方案中,为了使捐款最多,你选择哪种方案?
|手机型号|A|B|C|
|进价/(元/部)|1500|2100|2500|
|售价/(元/部)|1650|2300|2750|
若该手机卖场同时购进两种不同型号的手机共50台,9万元刚好用完.
(1)请你确定该手机卖场的进货方案,并说明理由;
(2)该卖场老板准备把这批手机销售利润的50%捐给公益组织,在同时购进两种不同型号手机的方案中,为了使捐款最多,你选择哪种方案?
答案:解:(1)①当购进A和B两种型号手机时,
设购进A型手机a台,则购进B型号手机(50-a)台,
根据题意得1500a+2100(50-a)=90000,解得a=25,
故可购进A型手机25台,购进B型号手机25台.
②当购进B和C两种型号手机时,
设购进B型号手机b台,则购进C型号手机(50-b)台,
根据题意得2100b+2500(50-b)=90000,
解得b=87.5>50,故舍去.
③当购进A和C两种型号手机时,
设购进C型号手机c台,则购进A型号手机(50-c)台,
根据题意得1500(50-c)+2500c=90000,解得c=15,
故可购进C型号手机15台,购进A型手机35台.
故有两种进货方案.
方案一:可购进A型手机25台,购进B型号手机25台;
方案二:可购进C型号手机15台,购进A型手机35台.
(2)方案一的利润:25×(1650-1500)+25×(2300-2100)=8750(元),捐款数额:8750×50%=4375(元);
方案二的利润:15×(2750-2500)+35×(1650-1500)=9000(元),捐款数额:9000×50%=4500(元).
因为4375<4500,
故选择方案二,即购进C型号手机15台,购进A型手机35台,可以使捐款最多.
设购进A型手机a台,则购进B型号手机(50-a)台,
根据题意得1500a+2100(50-a)=90000,解得a=25,
故可购进A型手机25台,购进B型号手机25台.
②当购进B和C两种型号手机时,
设购进B型号手机b台,则购进C型号手机(50-b)台,
根据题意得2100b+2500(50-b)=90000,
解得b=87.5>50,故舍去.
③当购进A和C两种型号手机时,
设购进C型号手机c台,则购进A型号手机(50-c)台,
根据题意得1500(50-c)+2500c=90000,解得c=15,
故可购进C型号手机15台,购进A型手机35台.
故有两种进货方案.
方案一:可购进A型手机25台,购进B型号手机25台;
方案二:可购进C型号手机15台,购进A型手机35台.
(2)方案一的利润:25×(1650-1500)+25×(2300-2100)=8750(元),捐款数额:8750×50%=4375(元);
方案二的利润:15×(2750-2500)+35×(1650-1500)=9000(元),捐款数额:9000×50%=4500(元).
因为4375<4500,
故选择方案二,即购进C型号手机15台,购进A型手机35台,可以使捐款最多.
13.(19分)点O是直线AB上一点,$∠COD$是直角,OE平分$∠BOC$.
(1)①如图①,若$∠DOE = 15^{\circ}$,求$∠AOC$的度数;
②如图②,若$∠DOE = \alpha$,求$∠AOC$的度数.(用含α的式子表示)
(2)将图①中的$∠COD$绕点O按顺时针方向旋转至图②所示的位置.探究$∠DOE与∠AOC$之间的数量关系,写出你的结论,并说明理由.
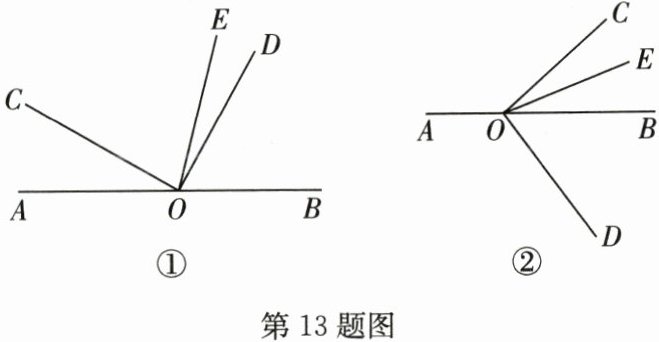
(1)①如图①,若$∠DOE = 15^{\circ}$,求$∠AOC$的度数;
②如图②,若$∠DOE = \alpha$,求$∠AOC$的度数.(用含α的式子表示)
(2)将图①中的$∠COD$绕点O按顺时针方向旋转至图②所示的位置.探究$∠DOE与∠AOC$之间的数量关系,写出你的结论,并说明理由.

答案:解:(1)①因为∠COD=90°,∠DOE=15°,
所以∠COE=∠COD-∠DOE=90°-15°=75°.
又因为OE平分∠BOC,
所以∠BOC=2∠COE=150°,
所以∠AOC=180°-∠BOC=180°-150°=30°.
②因为∠COD=90°,∠DOE=α,
所以∠COE=∠COD-∠DOE=90°-α.
又因为OE平分∠BOC,
所以∠BOC=2∠COE=180°-2α,
所以∠AOC=180°-∠BOC=180°-(180°-2α)=2α.
(2)∠DOE=$\frac{1}{2}$∠AOC,理由如下:
因为OE平分∠BOC,
所以∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(180°-∠AOC)=90°-$\frac{1}{2}$∠AOC.
又因为∠COD=90°,
所以∠DOE=90°-∠COE=90°-(90°-$\frac{1}{2}$∠AOC)=$\frac{1}{2}$∠AOC.
所以∠COE=∠COD-∠DOE=90°-15°=75°.
又因为OE平分∠BOC,
所以∠BOC=2∠COE=150°,
所以∠AOC=180°-∠BOC=180°-150°=30°.
②因为∠COD=90°,∠DOE=α,
所以∠COE=∠COD-∠DOE=90°-α.
又因为OE平分∠BOC,
所以∠BOC=2∠COE=180°-2α,
所以∠AOC=180°-∠BOC=180°-(180°-2α)=2α.
(2)∠DOE=$\frac{1}{2}$∠AOC,理由如下:
因为OE平分∠BOC,
所以∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(180°-∠AOC)=90°-$\frac{1}{2}$∠AOC.
又因为∠COD=90°,
所以∠DOE=90°-∠COE=90°-(90°-$\frac{1}{2}$∠AOC)=$\frac{1}{2}$∠AOC.