1. 计算$(\frac {11}{12}-\frac {7}{6}+\frac {3}{4}-\frac {13}{24})×(-24)$的结果是 (
A.1
B.-1
C.10
D.-10
A
)A.1
B.-1
C.10
D.-10
答案:A
解析:
解:$\begin{aligned}&(\frac{11}{12} - \frac{7}{6} + \frac{3}{4} - \frac{13}{24})×(-24)\\=&\frac{11}{12}×(-24) - \frac{7}{6}×(-24) + \frac{3}{4}×(-24) - \frac{13}{24}×(-24)\\=&-22 + 28 - 18 + 13\\=&( -22 - 18 ) + ( 28 + 13 )\\=&-40 + 41\\=&1\end{aligned}$
A
A
2. 以下等式变形不正确的是 (
A.由$x+2= y+2$,得到$x= y$
B.由$2a-3= b-3$,得到$2a= b$
C.由$am= an$,得到$m= n$
D.由$m= n$,得到$2am= 2an$
C
)A.由$x+2= y+2$,得到$x= y$
B.由$2a-3= b-3$,得到$2a= b$
C.由$am= an$,得到$m= n$
D.由$m= n$,得到$2am= 2an$
答案:C
解析:
解:A. 由$x + 2 = y + 2$,两边同时减2,得到$x = y$,变形正确。
B. 由$2a - 3 = b - 3$,两边同时加3,得到$2a = b$,变形正确。
C. 由$am = an$,当$a = 0$时,$m$不一定等于$n$,变形不正确。
D. 由$m = n$,两边同时乘$2a$,得到$2am = 2an$,变形正确。
答案:C
B. 由$2a - 3 = b - 3$,两边同时加3,得到$2a = b$,变形正确。
C. 由$am = an$,当$a = 0$时,$m$不一定等于$n$,变形不正确。
D. 由$m = n$,两边同时乘$2a$,得到$2am = 2an$,变形正确。
答案:C
3. 现定义运算“*”,对于任意有理数$a与b$,满足$a*b= \left\{\begin{array}{l} 3a-b,a≥b,\\ a-3b,a\lt b,\end{array} \right. $譬如,$5*3= 3×5-3= 12,\frac {1}{2}*1= \frac {1}{2}-3×1= -\frac {5}{2}$. 若有理数$x满足x*3= 12$,则$x$的值为 (
A.4
B.5
C.21
D.5或21
B
)A.4
B.5
C.21
D.5或21
答案:B
解析:
解:当$x\geq3$时,$x*3 = 3x - 3$,由$3x - 3 = 12$,得$3x=15$,$x = 5$,符合$x\geq3$。
当$x\lt3$时,$x*3 = x - 3×3$,由$x - 9 = 12$,得$x = 21$,不符合$x\lt3$,舍去。
综上,$x$的值为$5$。
答案:B
当$x\lt3$时,$x*3 = x - 3×3$,由$x - 9 = 12$,得$x = 21$,不符合$x\lt3$,舍去。
综上,$x$的值为$5$。
答案:B
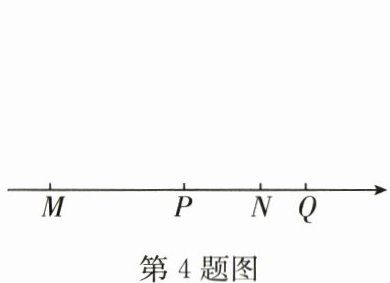
4. 如图,四个数在数轴上的对应点分别为点$M,P,N,Q$. 若点$M,N$表示的数互为相反数,则图中表示正数的点的个数是 (
A.1
B.2
C.3
D.4
C
) 
A.1
B.2
C.3
D.4
答案:C
解析:
解:因为点M,N表示的数互为相反数,所以原点是线段MN的中点。由数轴上点的位置M<P<N<Q可知,点M在原点左侧,表示负数;点N在原点右侧,表示正数;点P在M右侧、N左侧,且MN中点为原点,所以P在原点右侧,表示正数;点Q在N右侧,表示正数。因此,表示正数的点有P,N,Q,共3个。
答案:C
答案:C
5. 一副三角板按如图方式摆放,且$∠1的度数比∠2的度数小20^{\circ }$,则$∠1$的度数为 (
A.$35^{\circ }$
B.$30^{\circ }$
C.$25^{\circ }$
D.$20^{\circ }$
A
)A.$35^{\circ }$
B.$30^{\circ }$
C.$25^{\circ }$
D.$20^{\circ }$
答案:A
解析:
解:由图可知,∠1 + ∠2 = 90°
又∵∠1 = ∠2 - 20°
∴∠2 - 20° + ∠2 = 90°
解得∠2 = 55°
∴∠1 = 55° - 20° = 35°
答案:A
又∵∠1 = ∠2 - 20°
∴∠2 - 20° + ∠2 = 90°
解得∠2 = 55°
∴∠1 = 55° - 20° = 35°
答案:A
6. 数轴上$A,B$两点之间的距离为3,若点$A$表示数2,则点$B$表示的数为
-1或5
.答案:-1或5
解析:
解:设点$B$表示的数为$x$。
因为$A$,$B$两点之间的距离为$3$,点$A$表示数$2$,所以$|x - 2| = 3$。
当$x - 2 = 3$时,$x = 5$;
当$x - 2 = -3$时,$x = -1$。
故点$B$表示的数为$-1$或$5$。
因为$A$,$B$两点之间的距离为$3$,点$A$表示数$2$,所以$|x - 2| = 3$。
当$x - 2 = 3$时,$x = 5$;
当$x - 2 = -3$时,$x = -1$。
故点$B$表示的数为$-1$或$5$。
7. 若多项式$2y-x^{2}$的值为2,则多项式$2x^{2}-4y+7$的值为
3
.答案:3
解析:
解:由题意得,$2y - x^2 = 2$,则$x^2 - 2y = -2$。
$2x^2 - 4y + 7 = 2(x^2 - 2y) + 7$
将$x^2 - 2y = -2$代入上式,得:
$2×(-2) + 7 = -4 + 7 = 3$
3
$2x^2 - 4y + 7 = 2(x^2 - 2y) + 7$
将$x^2 - 2y = -2$代入上式,得:
$2×(-2) + 7 = -4 + 7 = 3$
3
8. 某种商品换季处理,若按标价的六五折出售,每件将亏损25元,而按标价的八折出售,每件将盈利20元,则这种商品的进价是
220
元/件.答案:220
解析:
解:设这种商品的标价为$x$元/件。
根据题意,得$0.65x + 25 = 0.8x - 20$
解得$x = 300$
则进价为$0.65×300 + 25 = 220$(元/件)
220
根据题意,得$0.65x + 25 = 0.8x - 20$
解得$x = 300$
则进价为$0.65×300 + 25 = 220$(元/件)
220
9. 如图是一个正方体的表面展开图,将展开图折叠成正方体后,相对面上两个数之和为5,则$x+y=$
4
.答案:4
10. 如图,$∠COD在∠AOB$内部,$OE平分∠BOD$. 若$∠AOB= m^{\circ },∠COD= n^{\circ }$,则$2∠AOE+∠BOC= $
2m-n
$^{\circ }$.(用含$m,n$的代数式表示)答案:2m-n