10. 规定如下两种运算:$x\otimes y= 2xy+1;x\oplus y= x+2y-1$. 例如:$2\otimes 3= 2×2×3+1= 13;2\oplus 3= 2+2×3-1= 7$. 若$a\otimes (4\oplus 5)$的值为79,则$3a+2[3a-2(2a-1)]$的值是
7
.答案:7
解析:
解:先计算$4\oplus5$,根据$x\oplus y = x + 2y - 1$,可得:
$4\oplus5=4 + 2×5 - 1=4 + 10 - 1=13$
因为$a\otimes(4\oplus5)=79$,即$a\otimes13=79$,又根据$x\otimes y = 2xy + 1$,所以:
$2×a×13 + 1=79$
$26a + 1=79$
$26a=78$
$a=3$
再计算$3a + 2[3a - 2(2a - 1)]$:
$\begin{aligned}&3a + 2[3a - 2(2a - 1)]\\=&3a + 2[3a - 4a + 2]\\=&3a + 2[-a + 2]\\=&3a - 2a + 4\\=&a + 4\end{aligned}$
将$a = 3$代入$a + 4$,得$3 + 4=7$
7
$4\oplus5=4 + 2×5 - 1=4 + 10 - 1=13$
因为$a\otimes(4\oplus5)=79$,即$a\otimes13=79$,又根据$x\otimes y = 2xy + 1$,所以:
$2×a×13 + 1=79$
$26a + 1=79$
$26a=78$
$a=3$
再计算$3a + 2[3a - 2(2a - 1)]$:
$\begin{aligned}&3a + 2[3a - 2(2a - 1)]\\=&3a + 2[3a - 4a + 2]\\=&3a + 2[-a + 2]\\=&3a - 2a + 4\\=&a + 4\end{aligned}$
将$a = 3$代入$a + 4$,得$3 + 4=7$
7
11. (12分)解下列方程:
(1)$4(2x-3)-(5x-1)= 7$; (2)$\frac {x-1}{3}-1= \frac {4-x}{2}$.
(1)$4(2x-3)-(5x-1)= 7$; (2)$\frac {x-1}{3}-1= \frac {4-x}{2}$.
答案:(1)$x=6$ (2)$x=4$
解析:
(1)解:$4(2x - 3) - (5x - 1) = 7$
$8x - 12 - 5x + 1 = 7$
$3x - 11 = 7$
$3x = 18$
$x = 6$
(2)解:$\frac{x - 1}{3} - 1 = \frac{4 - x}{2}$
$2(x - 1) - 6 = 3(4 - x)$
$2x - 2 - 6 = 12 - 3x$
$2x - 8 = 12 - 3x$
$5x = 20$
$x = 4$
$8x - 12 - 5x + 1 = 7$
$3x - 11 = 7$
$3x = 18$
$x = 6$
(2)解:$\frac{x - 1}{3} - 1 = \frac{4 - x}{2}$
$2(x - 1) - 6 = 3(4 - x)$
$2x - 2 - 6 = 12 - 3x$
$2x - 8 = 12 - 3x$
$5x = 20$
$x = 4$
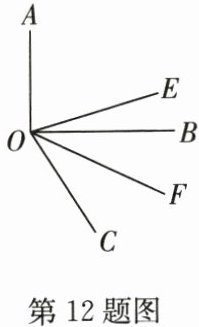
12. (10分)如图,已知$∠AOB$是直角,$∠BOC在∠AOB$的外部,且$OF平分∠BOC,OE平分∠AOC$.
(1)当$∠BOC= 60^{\circ }$时,求$∠EOF$的度数;
(2)当$∠BOE= 20^{\circ }$时,求$∠BOC$的度数.
(1)当$∠BOC= 60^{\circ }$时,求$∠EOF$的度数;
(2)当$∠BOE= 20^{\circ }$时,求$∠BOC$的度数.

答案:解:(1)∵∠AOB是直角,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=150°.
∵OE平分∠AOC,∴∠EOC=$\frac{1}{2}$∠AOC=75°.
∵OF平分∠BOC,∴∠FOC=$\frac{1}{2}$∠BOC=30°.
∴∠EOF=∠EOC−∠FOC=75°−30°=45°.
(2)∵∠BOE=20°,∠AOB是直角,
∴∠AOE=∠AOB−∠BOE=70°,
∵OE平分∠AOC,∴∠EOC=∠AOE=70°,
∴∠BOC=∠EOC−∠BOE=70°−20°=50°.
∴∠AOC=∠AOB+∠BOC=150°.
∵OE平分∠AOC,∴∠EOC=$\frac{1}{2}$∠AOC=75°.
∵OF平分∠BOC,∴∠FOC=$\frac{1}{2}$∠BOC=30°.
∴∠EOF=∠EOC−∠FOC=75°−30°=45°.
(2)∵∠BOE=20°,∠AOB是直角,
∴∠AOE=∠AOB−∠BOE=70°,
∵OE平分∠AOC,∴∠EOC=∠AOE=70°,
∴∠BOC=∠EOC−∠BOE=70°−20°=50°.
13. (12分)一家服装店购进100件衣服,加价$40\%$后作为售价. 售出了60件后,剩下的40件按售价打对折售完,结果盈利6000元.
(1)这批衣服每件的进价为多少元?
(2)售完全部衣服后,店主将与购进这批衣服的货款等额的钱(不包括盈利部分)存入银行,存期一年,得到的利息为1500元,那么银行一年定期的利率为多少?
(1)这批衣服每件的进价为多少元?
(2)售完全部衣服后,店主将与购进这批衣服的货款等额的钱(不包括盈利部分)存入银行,存期一年,得到的利息为1500元,那么银行一年定期的利率为多少?
答案:解:(1)设这批衣服每件的进价为x元,则原售价是1.4x元,根据题意,得
1.4x×60+0.5×1.4x×40−100x=6000,解得x=500.答:这批衣服每件的进价为500元.
(2)设银行一年定期的利率是y,根据题意得
100×500y×1=1500,解得y=3%.
答:银行一年定期的利率是3%.
1.4x×60+0.5×1.4x×40−100x=6000,解得x=500.答:这批衣服每件的进价为500元.
(2)设银行一年定期的利率是y,根据题意得
100×500y×1=1500,解得y=3%.
答:银行一年定期的利率是3%.
14. (16分)如图,$P是线段AB$上一点,$AB= 12cm,M,N两点分别从点P,B$出发,以$1cm/s,3cm/s$的速度同时向左运动(点$M在线段AP$上,点$N在线段BP$上),运动时间为$ts$.
(1)当点$M,N运动1s$时,$PN= 3AM$,求$AP$的长.
(2)若点$M,N$运动到任一时刻时,总有$PN= 3AM$,线段$AP$的长度是否变化? 若不变,请求出线段$AP$的长;若变化,请说明理由.
(3)在(2)的条件下,$Q是直线AB$上一点,且$AQ= PQ+BQ$,求线段$PQ$的长.

(1)当点$M,N运动1s$时,$PN= 3AM$,求$AP$的长.
(2)若点$M,N$运动到任一时刻时,总有$PN= 3AM$,线段$AP$的长度是否变化? 若不变,请求出线段$AP$的长;若变化,请说明理由.
(3)在(2)的条件下,$Q是直线AB$上一点,且$AQ= PQ+BQ$,求线段$PQ$的长.

答案:
解:(1)根据点M,N的运动速度可知,当点M,N运动1s 时,BN=3cm,PM=1cm.
因为AM+MP+PN+BN=AB,且PN=3AM,
所以AM+1+3AM+3=12,
所以AM=2cm,所以AP=3cm.
(2)线段AP的长度不发生变化.
根据点M,N的运动速度可知,BN=3PM;
因为AM+MP+PN+BN=AB,且PN=3AM,
所以4AM+4PM=12,
所以AP=AM+PM=3(cm).
(3)当点Q在线段AB上时,如答图.

因为AQ=AP+PQ,AQ=PQ+BQ,
所以AP=BQ=3cm,
所以PQ=AB−AP−BQ=12−3−3=6(cm);
当点Q在线段AB的延长线或反向延长线上时,
因为AQ=PQ+BQ,
所以点Q在线段AB的延长线上,
又因为AQ=AP+PQ,所以BQ=AP=3cm,
所以PQ=PB+BQ=AB−AP+BQ=AB=12(cm).综上所述,线段PQ的长为6cm或12cm
解:(1)根据点M,N的运动速度可知,当点M,N运动1s 时,BN=3cm,PM=1cm.
因为AM+MP+PN+BN=AB,且PN=3AM,
所以AM+1+3AM+3=12,
所以AM=2cm,所以AP=3cm.
(2)线段AP的长度不发生变化.
根据点M,N的运动速度可知,BN=3PM;
因为AM+MP+PN+BN=AB,且PN=3AM,
所以4AM+4PM=12,
所以AP=AM+PM=3(cm).
(3)当点Q在线段AB上时,如答图.

因为AQ=AP+PQ,AQ=PQ+BQ,
所以AP=BQ=3cm,
所以PQ=AB−AP−BQ=12−3−3=6(cm);
当点Q在线段AB的延长线或反向延长线上时,
因为AQ=PQ+BQ,
所以点Q在线段AB的延长线上,
又因为AQ=AP+PQ,所以BQ=AP=3cm,
所以PQ=PB+BQ=AB−AP+BQ=AB=12(cm).综上所述,线段PQ的长为6cm或12cm