1. 下表是某年 10 月的月历,观察月历,回答问题:
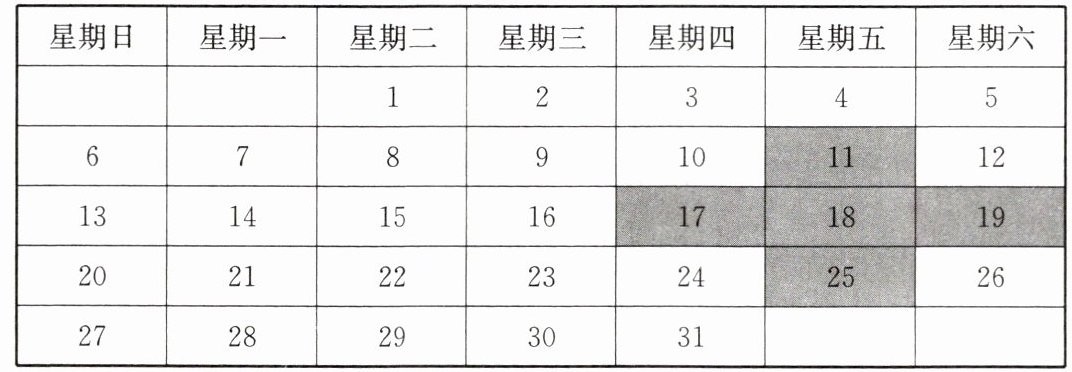
(1) 小艳国庆假期外出旅行三天,三天日期之和是 12,小艳是星期几出发的?
(2) “十字形”阴影覆盖其中五个方格,设“十字形”阴影覆盖的最小数为 $ x $,五个数之和为 $ S $. $ S $ 的值能否等于 75?若能,求出 $ x $ 的值;若不能,请说明理由.

(1) 小艳国庆假期外出旅行三天,三天日期之和是 12,小艳是星期几出发的?
星期四
(2) “十字形”阴影覆盖其中五个方格,设“十字形”阴影覆盖的最小数为 $ x $,五个数之和为 $ S $. $ S $ 的值能否等于 75?若能,求出 $ x $ 的值;若不能,请说明理由.
S的值能等于75,x=8
答案:1.解:(1)设小艳出发的日期是x,则另外两天的日期分别是(x+1),(x+2).
根据题意,得x+x+1+x+2=12,
解得x=3.
答:小艳是星期四出发的.
(2)S的值能等于75.理由如下:
假设S的值能等于75,
因为“十字形”阴影覆盖的最小数为x,
所以“十字形”阴影覆盖的另外四个数分别为(x+7),(x+6),(x+8),(x+14).根据题意,得x+(x+7)+(x+6)+(x+8)+(x+14)=75,
解得x=8.
因为10月8日是星期二,在第三列,此时能形成“十字形”阴影,
所以x=8符合题意,
所以假设成立,即S的值能等于75.
根据题意,得x+x+1+x+2=12,
解得x=3.
答:小艳是星期四出发的.
(2)S的值能等于75.理由如下:
假设S的值能等于75,
因为“十字形”阴影覆盖的最小数为x,
所以“十字形”阴影覆盖的另外四个数分别为(x+7),(x+6),(x+8),(x+14).根据题意,得x+(x+7)+(x+6)+(x+8)+(x+14)=75,
解得x=8.
因为10月8日是星期二,在第三列,此时能形成“十字形”阴影,
所以x=8符合题意,
所以假设成立,即S的值能等于75.
2. 如图,图①是某年 10 月的月历.
(1) 如图①所示,用一个框竖着框住三个数,若被框住的三个数的和为 60,则竖框中第一行的数为______
(2) 如图①所示,若在月历中任意画一个十字框,框住五个数,设这五个数分别为 $ a,b,c,d,e $,具体见图②,若 $ a + b + c + d = 48 $,求 $ e $ 的值.
(3) 在月历中画的十字框如图②,是否存在 $ e $ 的值,使得 $ a + b + c + d = 100 $?请说明理由.
(1) 如图①所示,用一个框竖着框住三个数,若被框住的三个数的和为 60,则竖框中第一行的数为______
13
.(2) 如图①所示,若在月历中任意画一个十字框,框住五个数,设这五个数分别为 $ a,b,c,d,e $,具体见图②,若 $ a + b + c + d = 48 $,求 $ e $ 的值.
解:根据题意,得a=e-7,b=e-1,c=e+7,d=e+1,所以a+b+c+d=(e-7)+(e-1)+(e+7)+(e+1)=4e=48,解得e=12.所以e的值为12.
(3) 在月历中画的十字框如图②,是否存在 $ e $ 的值,使得 $ a + b + c + d = 100 $?请说明理由.
解:不存在e的值,使得a+b+c+d=100.理由如下,假设存在,根据题意,得4e=100,解得e=25,所以c=e+7=25+7=32.因为32>31,所以假设不成立,即不存在e的值,使得a+b+c+d=100.
答案:2.(1)13
点拨:设中间的数为x,则另外两个数分别为x-7,x+7.
根据题意,得x-7+x+x+7=60,解得x=20,所以x-7=20-7=13,x+7=20+7=27,故这三个数分别为13,20,27.
(2)解:根据题意,得a=e-7,b=e-1,c=e+7,d=e+1,所以a+b+c+d=(e-7)+(e-1)+(e+7)+(e+1)=4e=48,
解得e=12.
所以e的值为12.
(3)解:不存在e的值,使得a+b+c+d=100.理由如下,假设存在,根据题意,得4e=100,
解得e=25,
所以c=e+7=25+7=32.
因为32>31,所以假设不成立,
即不存在e的值,使得a+b+c+d=100.
点拨:设中间的数为x,则另外两个数分别为x-7,x+7.
根据题意,得x-7+x+x+7=60,解得x=20,所以x-7=20-7=13,x+7=20+7=27,故这三个数分别为13,20,27.
(2)解:根据题意,得a=e-7,b=e-1,c=e+7,d=e+1,所以a+b+c+d=(e-7)+(e-1)+(e+7)+(e+1)=4e=48,
解得e=12.
所以e的值为12.
(3)解:不存在e的值,使得a+b+c+d=100.理由如下,假设存在,根据题意,得4e=100,
解得e=25,
所以c=e+7=25+7=32.
因为32>31,所以假设不成立,
即不存在e的值,使得a+b+c+d=100.