1. 有公共端点的
2. 角的表示方法:(1)三个
3. 角的度量与单位:
1 周角=
两条射线
组成的图形叫作角,角也可以看作是一条射线绕着它的端点旋转
而形成的图形。2. 角的表示方法:(1)三个
大写
字母,顶点必须写在中间
;(2)一个大写字母;(3)一个数字或希腊字母。3. 角的度量与单位:
1 周角=
360
${}^{\circ }$;1 平角=180
${}^{\circ }$;$1^{\circ }=$60
$'$;$1'= $60
$''$。答案:1. 两条射线 旋转 2. (1)大写 中间 3. 360 180 60 60
1. $∠ABC$可以表示下面的 (
C
)答案:C
2. 如图,下列说法不正确的是 (
A.$∠1与∠AOB$是同一个角
B.$∠AOC也可以用∠O$表示
C.$∠β=∠BOC$
D.图中有三个角
B
)A.$∠1与∠AOB$是同一个角
B.$∠AOC也可以用∠O$表示
C.$∠β=∠BOC$
D.图中有三个角
答案:B
3. 如图,图中包含的小于平角的角有 (
A.5 个
B.6 个
C.7 个
D.8 个
C
)A.5 个
B.6 个
C.7 个
D.8 个
答案:C
解析:
图中小于平角的角有:∠B,∠BAC,∠CAD,∠BAD,∠ACB,∠ACD,∠D,共7个。
C
C
4. 把$10^{\circ }36''$用度表示为 (
A.$10.6^{\circ }$
B.$10.001^{\circ }$
C.$10.01^{\circ }$
D.$10.1^{\circ }$
C
)A.$10.6^{\circ }$
B.$10.001^{\circ }$
C.$10.01^{\circ }$
D.$10.1^{\circ }$
答案:C
解析:
因为$1^{\circ}=60'$,$1'=60''$,所以$36''=\left(\dfrac{36}{60}\right)'=0.6'$,$0.6'=\left(\dfrac{0.6}{60}\right)^{\circ}=0.01^{\circ}$,则$10^{\circ}36''=10^{\circ}+0.01^{\circ}=10.01^{\circ}$。
C
C
5. A,B 两栋教学楼的位置如图所示,那么 B 教学楼在 A 教学楼的
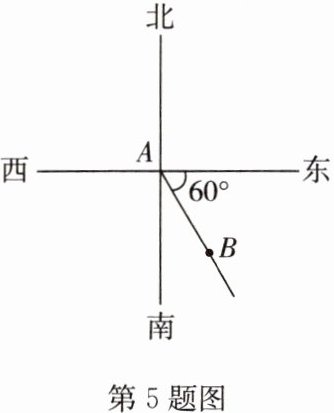
南偏东 $30^\circ$(或东偏南 $60^\circ$)
位置。
答案:南偏东 $30^\circ$(或东偏南 $60^\circ$)