1. 如果两个角的和等于$90^{\circ }$(直角),就说这两个角互为
2. 同角(或等角)的余角
3. 已知$∠1= 25^{\circ }$,则$∠1$的余角的度数为
4. 若$∠1+∠2= 90^{\circ },∠3+∠4= 90^{\circ }$,且$∠1= ∠3$,则$∠2与∠4$的关系为
余角
;如果两个角的和等于$180^{\circ }$(平角),就说这两个角互为补角
.2. 同角(或等角)的余角
相等
;同角(或等角)的补角相等
.3. 已知$∠1= 25^{\circ }$,则$∠1$的余角的度数为
65°
,$∠1$的补角的度数为155°
.4. 若$∠1+∠2= 90^{\circ },∠3+∠4= 90^{\circ }$,且$∠1= ∠3$,则$∠2与∠4$的关系为
∠2=∠4
.答案:1.余角 补角 2.相等 相等 3.65° 155° 4.∠2=∠4
解析:
1. $45^{\circ }$的余角是 (
A.$45^{\circ }$
B.$90^{\circ }$
C.$135^{\circ }$
D.$180^{\circ }$
A
)A.$45^{\circ }$
B.$90^{\circ }$
C.$135^{\circ }$
D.$180^{\circ }$
答案:A
解析:
$90^{\circ}-45^{\circ}=45^{\circ}$,A
2. 若一个角为$75^{\circ }$,则它的补角的度数为 (
A.$35^{\circ }$
B.$45^{\circ }$
C.$105^{\circ }$
D.$115^{\circ }$
C
)A.$35^{\circ }$
B.$45^{\circ }$
C.$105^{\circ }$
D.$115^{\circ }$
答案:C
解析:
$180^{\circ}-75^{\circ}=105^{\circ}$
C
C
3. 若$∠α与∠β$互为补角,则下列式子成立的是 (
A.$∠α-∠β= 180^{\circ }$
B.$∠α+∠β= 90^{\circ }$
C.$∠α-∠β= 90^{\circ }$
D.$∠α+∠β= 180^{\circ }$
D
)A.$∠α-∠β= 180^{\circ }$
B.$∠α+∠β= 90^{\circ }$
C.$∠α-∠β= 90^{\circ }$
D.$∠α+∠β= 180^{\circ }$
答案:D
4. 如图,$∠1和∠2都是∠α$的余角,则下列关系不正确的是 (
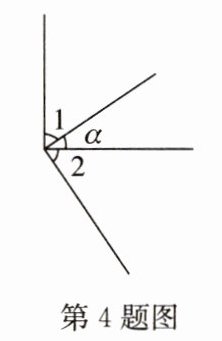
A.$∠1+∠α= 90^{\circ }$
B.$∠2+∠α= 90^{\circ }$
C.$∠1= ∠2$
D.$∠1+∠2= 90^{\circ }$
D
)
A.$∠1+∠α= 90^{\circ }$
B.$∠2+∠α= 90^{\circ }$
C.$∠1= ∠2$
D.$∠1+∠2= 90^{\circ }$
答案:D
解析:
因为∠1和∠2都是∠α的余角,所以∠1+∠α=90°,∠2+∠α=90°,故A、B正确;由同角的余角相等,可得∠1=∠2,故C正确;∠1+∠2=2∠1=2(90°-∠α)=180°-2∠α,只有当∠α=45°时,∠1+∠2=90°,故D不正确。
D
D
5. 如图,将两块相同的直角三角板的直角顶点重合.若$∠AOC= 15^{\circ }$,则$∠BOD$的度数是 (
A.$15^{\circ }$
B.$25^{\circ }$
C.$75^{\circ }$
D.$85^{\circ }$
A
)A.$15^{\circ }$
B.$25^{\circ }$
C.$75^{\circ }$
D.$85^{\circ }$
答案:A
解析:
因为两块直角三角板直角顶点重合,所以∠AOB=∠COD=90°。
∠AOB=∠AOC+∠COB,∠COD=∠COB+∠BOD,
所以∠AOC+∠COB=∠COB+∠BOD,
因此∠AOC=∠BOD。
因为∠AOC=15°,所以∠BOD=15°。
A
∠AOB=∠AOC+∠COB,∠COD=∠COB+∠BOD,
所以∠AOC+∠COB=∠COB+∠BOD,
因此∠AOC=∠BOD。
因为∠AOC=15°,所以∠BOD=15°。
A
6. 如果$∠AOB+∠BOC= 180^{\circ }$,且$∠BOC与∠COD$互补,那么$∠AOB与∠COD$的关系是 (
A.互余
B.互补
C.相等
D.不能确定
C
)A.互余
B.互补
C.相等
D.不能确定
答案:C
解析:
因为∠AOB+∠BOC=180°,所以∠AOB=180°-∠BOC。
因为∠BOC与∠COD互补,所以∠BOC+∠COD=180°,即∠COD=180°-∠BOC。
所以∠AOB=∠COD。
C
因为∠BOC与∠COD互补,所以∠BOC+∠COD=180°,即∠COD=180°-∠BOC。
所以∠AOB=∠COD。
C
7. 如图,将一副直角三角板叠在一起,使直角顶点重合于点 O. 若$∠AOB= 155^{\circ }$,则$∠COD= $ (
A.$155^{\circ }$
B.$65^{\circ }$
C.$45^{\circ }$
D.$25^{\circ }$
D
)A.$155^{\circ }$
B.$65^{\circ }$
C.$45^{\circ }$
D.$25^{\circ }$
答案:D
解析:
由题意知,两直角三角板直角顶点重合于点$O$,则$\angle AOD + \angle DOC = 90^{\circ}$,$\angle COB + \angle DOC = 90^{\circ}$,所以$\angle AOD + \angle DOC + \angle COB + \angle DOC = 180^{\circ}$,即$\angle AOB + \angle COD = 180^{\circ}$。
因为$\angle AOB = 155^{\circ}$,所以$\angle COD = 180^{\circ} - \angle AOB = 180^{\circ} - 155^{\circ} = 25^{\circ}$。
D
因为$\angle AOB = 155^{\circ}$,所以$\angle COD = 180^{\circ} - \angle AOB = 180^{\circ} - 155^{\circ} = 25^{\circ}$。
D