1. 下图是学校创意班为“学校时装秀”设计的平面图,计算下面各个图形的面积。(单位：厘米)
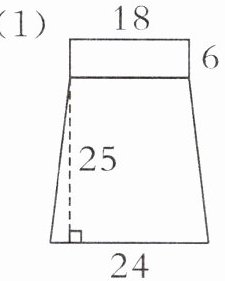
(1)
(2)
(3)
(1)
(2)
(3)
答案：1.
(1)(18+24)×25÷2+18×6=633(平方厘米)
(2)(16+24)×25÷2×2+24×6=1144(平方厘米)
(3)16×6+(16+7×4)×24÷2+7×(32 - 24)÷2×4=736(平方厘米)
[提示]利用分割求和的方法计算面积。
(1)(18+24)×25÷2+18×6=633(平方厘米)
(2)(16+24)×25÷2×2+24×6=1144(平方厘米)
(3)16×6+(16+7×4)×24÷2+7×(32 - 24)÷2×4=736(平方厘米)
[提示]利用分割求和的方法计算面积。
2. 填一填。
(1)如右图,连接平行四边形四条边的中点,可得到一个新的平行四边形,已知涂色部分的面积是24平方厘米,则大平行四边形的面积是(
(2)如右图,两个正方形的边长分别为10厘米和8厘米,涂色部分三角形的面积是(
(1)如右图,连接平行四边形四条边的中点,可得到一个新的平行四边形,已知涂色部分的面积是24平方厘米,则大平行四边形的面积是(
48
)平方厘米。(2)如右图,两个正方形的边长分别为10厘米和8厘米,涂色部分三角形的面积是(
50
)平方厘米。答案：2.
(1)48 [提示]因为涂色部分是由平行四边形四条边的中点连接起来的，即涂色部分的面积等于空白部分的面积，所以原平行四边形的面积是涂色部分面积的2倍。
(2)50 [提示]观察图形可知，涂色部分的面积=两个正方形的面积和 - 两个空白三角形的面积 + 右上角小三角形的面积。
(1)48 [提示]因为涂色部分是由平行四边形四条边的中点连接起来的，即涂色部分的面积等于空白部分的面积，所以原平行四边形的面积是涂色部分面积的2倍。
(2)50 [提示]观察图形可知，涂色部分的面积=两个正方形的面积和 - 两个空白三角形的面积 + 右上角小三角形的面积。
3. 如图,正方形的边长为10厘米,$AE= 8$厘米,$CF= 6$厘米,求涂色部分的面积。
答案：3.10×10 - 10×8÷2 - 10×6÷2=30(平方厘米)
[提示]观察图形可知，涂色部分的面积=正方形的面积 - 两个空白三角形的面积。
[提示]观察图形可知，涂色部分的面积=正方形的面积 - 两个空白三角形的面积。
4. 新考法 操作探究 下图中正方形的边长是12厘米,空白部分是一个三角形,涂色部分的面积是多少？
(1)上面框里是两名同学的做法,请你在做法正确的同学的名字后面画“√”。
(2)欢欢同学是这样做的：
$(3+12)×12÷2= 90$(平方厘米)
欢欢的方法是正确的吗？请说明理由。
(1)上面框里是两名同学的做法,请你在做法正确的同学的名字后面画“√”。
(2)欢欢同学是这样做的：
$(3+12)×12÷2= 90$(平方厘米)
欢欢的方法是正确的吗？请说明理由。
答案：
4.
(1)明明(√) 丽丽(√)
(2)欢欢的方法是正确的。
理由:如图，假设左面的梯形的高为$ h_1 $厘米，右面的梯形的高为$ h_2 $厘米，则:
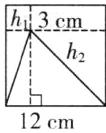(3+12)×$ h_1 $÷2+(3+12)×$ h_2 $÷2=(3+12)×($ h_1 $+$ h_2 $)÷2=(3+12)×12÷2=90(平方厘米)
所以欢欢的方法是正确的。
[提示]涂色部分可以看作两个下底、上底分别相等的梯形。因此可以用一个梯形的上、下底的和乘这两个梯形高的和再除以2，即可得到涂色部分的面积。
4.
(1)明明(√) 丽丽(√)
(2)欢欢的方法是正确的。
理由:如图，假设左面的梯形的高为$ h_1 $厘米，右面的梯形的高为$ h_2 $厘米，则:
(3+12)×$ h_1 $÷2+(3+12)×$ h_2 $÷2=(3+12)×($ h_1 $+$ h_2 $)÷2=(3+12)×12÷2=90(平方厘米)所以欢欢的方法是正确的。
[提示]涂色部分可以看作两个下底、上底分别相等的梯形。因此可以用一个梯形的上、下底的和乘这两个梯形高的和再除以2，即可得到涂色部分的面积。
5. 求图中涂色部分的面积。
答案：5.5×(3+3)÷2=15(平方厘米)
3×(5+5)÷2=15(平方厘米)
15÷3=5(平方厘米)
(3+3)×(5+5) - 5×4=40(平方厘米)
[提示]因为AD=DB,AE=EC,所以三角形ADF的面积=三角形BDF的面积，三角形AEF的面积=三角形CEF的面积。又因为三角形ABE的面积=5×(3+3)÷2=15(平方厘米)，三角形ACD的面积=3×(5+5)÷2=15(平方厘米)，所以三角形BDF的面积和三角形CEF的面积相等，即每个小三角形的面积=15÷3=5(平方厘米)。由此可知涂色部分的面积是(3+3)×(5+5) - 5×4=40(平方厘米)。
3×(5+5)÷2=15(平方厘米)
15÷3=5(平方厘米)
(3+3)×(5+5) - 5×4=40(平方厘米)
[提示]因为AD=DB,AE=EC,所以三角形ADF的面积=三角形BDF的面积，三角形AEF的面积=三角形CEF的面积。又因为三角形ABE的面积=5×(3+3)÷2=15(平方厘米)，三角形ACD的面积=3×(5+5)÷2=15(平方厘米)，所以三角形BDF的面积和三角形CEF的面积相等，即每个小三角形的面积=15÷3=5(平方厘米)。由此可知涂色部分的面积是(3+3)×(5+5) - 5×4=40(平方厘米)。