2025年实验班提优训练五年级数学上册苏教版第75页解析答案

(1)红红有5元和10元的两种纸币各10张,她要从中拿出35元,有(

)种拿法。

答案：4 【提示】35=5×1+10×3=5×3+10×2=5×5+10×1=5×7

(2)一列动车在上海与南京之间往返行驶,中间停靠苏州、无锡和常州,则这列动车应准备(

)种不同的车票。

答案：20 【提示】根据题意,可以画出下面的线段图。上海苏州无锡常州南京我们可以采用数线段的方法。上海往南京方向,一共要准备4+3+2+1=10(种)不同的车票;同样,南京往上海方向,也要准备10种不同的车票。所以应准备10+10=20(种)不同的车票。

解析：

上海到南京方向：4+3+2+1=10（种）
南京到上海方向：4+3+2+1=10（种）
共准备车票：10+10=20（种）
20

(3)一次数学竞赛共有5题,规定答对一题得4分,不答或者答错倒扣1分。丁丁参加这次数学竞赛,有(

)种可能的得分。

答案：6 【提示】列表如下:答对题数 5 4 3 2 1 0不答或答错题数 0 1 2 3 4 5得分 20 15 10 5 0 -5

2. 图中一共有多少个三角形？

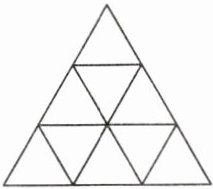
答案：设每个小等边三角形边长为1。①边长为1的三角形有:1+3+5=9(个);②边长为2的三角形有3个;③边长为3的三角形有1个。所以图中共有三角形:9+3+1=13(个)。【提示】把三角形按照边长大小分类,从最小的边长1开始,到最大的边长3为止。

解析：

设每个小等边三角形边长为1。
①边长为1的三角形：$1+3+5=9$（个）；
②边长为2的三角形：3个；
③边长为3的三角形：1个。
共有三角形：$9+3+1=13$（个）。

3. 图中有多少个正方形包含“☆”？

答案：1+4+6+3=14(个)【提示】把每个小正方形的边长看作1,边长为1且包含“☆”的正方形有1个,边长为2且包含“☆”的正方形有4个,边长为3且包含“☆”的正方形有6个,边长为4且包含“☆”的正方形有3个,这样可求出包含“☆”的正方形的总个数。

解析：

边长为1且包含“☆”的正方形：1个
边长为2且包含“☆”的正方形：4个
边长为3且包含“☆”的正方形：6个
边长为4且包含“☆”的正方形：3个
总个数：1+4+6+3=14(个)

4. 2026年足球世界杯将在美国、加拿大和墨西哥举办。48支球队分为12个小组,组内进行单循环赛,每组前两名和8个小组成绩最好的第三名进入淘汰赛。淘汰赛共32支球队进行单场淘汰,其中加一场季军和第四名争夺赛。从小组赛到淘汰赛一共比赛多少场？

答案：小组循环赛:6×12=72(场)淘汰赛:32-1=31(场)72+31+1=104(场)【提示】小组循环赛每组6场,12组就是72场。淘汰赛,第一轮比赛16场,第二轮比赛8场,第三轮4场,第四轮2场,第五轮2场(含季军和第四名比赛),16+8+4+2+2=32(场)。一共104场。

解析：

小组赛：每组单循环赛，每组有$4$支球队，比赛场数为$\frac{4×(4 - 1)}{2}=6$场，$12$个小组共$6×12 = 72$场。
淘汰赛：$32$支球队单场淘汰决出冠军需$32 - 1=31$场，加季军赛$1$场，共$31 + 1=32$场。
总比赛场数：$72+32 = 104$场。
答：从小组赛到淘汰赛一共比赛$104$场。

5. 下面图形中共有多少个正方形？