1. 根据钉子板中图形的信息完成填空。(涂色部分正方形的边长是1厘米)
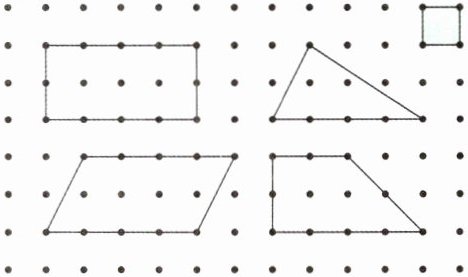
(1)长方形的长是(
(2)三角的底是(
(3)平行四边形的底是(
(4)梯形的上底是(
(1)长方形的长是(
4
)厘米,宽是(2
)厘米,面积是(8
)平方厘米。(2)三角的底是(
4
)厘米,高是(2
)厘米,面积是(4
)平方厘米。(3)平行四边形的底是(
4
)厘米,高是(2
)厘米,面积是(8
)平方厘米。(4)梯形的上底是(
2
)厘米,下底是(4
)厘米,高是(2
)厘米,面积是(6
)平方厘米。答案：1.
(1)4 2 8
(2)4 2 4
(3)4 2 8
(4)2 4 2 6
(1)4 2 8
(2)4 2 4
(3)4 2 8
(4)2 4 2 6
2. 在右下面的格点图(单位：厘米)中,宝塔图形的面积是多少平方厘米？
答案：2.11平方厘米 [提示]可以把宝塔图形分割成一个三角形、一个正方形和一个长方形，三角形的面积是2×3÷2=3(平方厘米);正方形的面积是2×2=4(平方厘米);长方形的面积是4×1=4(平方厘米)。宝塔图形的面积是3+4+4=11(平方厘米)。
解析：
三角形面积：$2×3÷2 = 3$（平方厘米）
正方形面积：$2×2 = 4$（平方厘米）
长方形面积：$4×1 = 4$（平方厘米）
总面积：$3 + 4 + 4 = 11$（平方厘米）
11平方厘米
正方形面积：$2×2 = 4$（平方厘米）
长方形面积：$4×1 = 4$（平方厘米）
总面积：$3 + 4 + 4 = 11$（平方厘米）
11平方厘米
3. 右下图是一个等边三角形格点图,共有21个点,其中每相邻的3个点构成的等边三角形的面积都为1平方厘米。
请
你
计算图中三角形的面积。答案：3.10平方厘米 [提示]图形内的格点数是4，边上的格点数是4，则图形的面积是$(4+4÷ 2-1)× 2=10$(平方厘米)。
4. 观察图中四个多边形,计算各多边形的面积,并统计每个多边形边上的格点数和图形内的格点数。
如果用S表示面积,N表示图形内的格点数,L表示图形边上的格点数,那么完成下面的统计表。
分析上表中的数据,你能发现任何一个多边形的面积与图形内的格点数及边上的格点数有什么联系吗？
如果用S表示面积,N表示图形内的格点数,L表示图形边上的格点数,那么完成下面的统计表。
分析上表中的数据,你能发现任何一个多边形的面积与图形内的格点数及边上的格点数有什么联系吗？
① $2\ \text{cm}^2$ 1 4 ② $4\ \text{cm}^2$ 2 6 ③ $7\ \text{cm}^2$ 5 6 ④ $9\ \text{cm}^2$ 6 8 发现:任何一个多边形的面积都等于图形内部的格点数加上边上的格点数除以2的和，再减1，即$S=N+L÷ 2-1$
答案：4. 图形 S N L ① $2\ \text{cm}^2$ 1 4 ② $4\ \text{cm}^2$ 2 6 ③ $7\ \text{cm}^2$ 5 6 ④ $9\ \text{cm}^2$ 6 8 发现:任何一个多边形的面积都等于图形内部的格点数加上边上的格点数除以2的和，再减1，即$S=N+L÷ 2-1$。[提示]观察图形完成统计表，分析表中的数据，不难发现任何一个多边形的面积都等于图形内的格点数加上边上的格点数除以2的和，再减1。
解析：
|图形|S|N|L|
|①|$2\ \text{cm}^2$|1|4|
|②|$4\ \text{cm}^2$|2|6|
|③|$7\ \text{cm}^2$|5|6|
|④|$9\ \text{cm}^2$|6|8|
发现：$S=N+\frac{L}{2}-1$
|①|$2\ \text{cm}^2$|1|4|
|②|$4\ \text{cm}^2$|2|6|
|③|$7\ \text{cm}^2$|5|6|
|④|$9\ \text{cm}^2$|6|8|
发现：$S=N+\frac{L}{2}-1$
5. 在下面的点子图上画出2个面积是12平方厘米的多边形,要求每个图形的形状都不相同。(每横排、竖列相邻两点之间的距离都是1厘米)
答案：
5.答案不唯一，如图: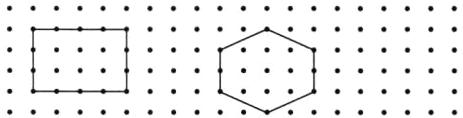
[提示]解决此类题的关键是根据公式数好图形内部及边上的点子数。
5.答案不唯一，如图:
[提示]解决此类题的关键是根据公式数好图形内部及边上的点子数。