1. 填一填。
(1)把一张平行四边形纸剪拼成一个长方形,周长,面积。把一个平行四边形框架推拉成一个长方形,周长,面积。(填“不变”“变大”或“变小”)
(2)如果将平行四边形的底扩大到原来的4倍,高缩小到原来的$\frac{1}{2}$,那么面积;如果它的底缩小到原来的$\frac{1}{3}$,高扩大到原来的3倍,那么面积。

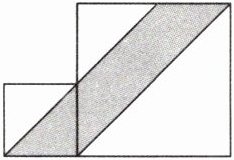
(1)如下图,涂色部分平行四边形的面积是96平方厘米,大正方形的边长是16厘米,那么小正方形的边长是()厘米。

A.6
B.12
C.3
D.4

(2)下面图形()中涂色部分的面积和图形①中的涂色部分的面积相等。(四个正方形同样大)
A.②③
B.②④
C.③④
D.②③④

3. 手工课上,老师让大家折自己喜欢的形状。雨桐用一张长10厘米的长方形彩纸按如图所示进行翻折,翻折的部分完全一样,发现折出的平行四边形面积比原来少15平方厘米。这张长方形纸的面积是多少平方厘米?

4. 画出图中三角形面积的$\frac{1}{3}$,再涂上颜色。
[我思考] 画出三角形面积的$\frac{1}{3}$,如果高不变,面积与有关系;如果底不变,面积与有关系。(填“底”或“高”)
[我验证] (1)先算出原来三角形的面积是平方厘米。如果高不变,那么新三角形的面积是原来的$\frac{1}{3}$,底是,也就是的$\frac{1}{3}$。新三角形的面积是平方厘米。
(2)先算出原来三角形的面积是平方厘米。如果底不变,那么新三角形的面积是原来的$\frac{1}{3}$,高是,也就是的$\frac{1}{3}$。新三角形的面积是平方厘米。
[我发现] 求一个三角形面积的$\frac{1}{3}$是多少,若底不变,则求的$\frac{1}{3}$;若高不变,则求的$\frac{1}{3}$。