4. 小明用火柴棒摆出下面的图形。
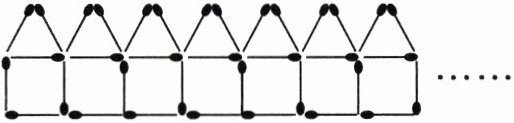
(1)搭一个房子需要几根火柴棒? 两个房子? 七个房子呢?n个房子呢?
1个房子= ( )根
2个房子= ( )根
7个房子= ( )根
n个房子= ( )根
(2)当$n= 99$时,需要多少根小棒?

(1)搭一个房子需要几根火柴棒? 两个房子? 七个房子呢?n个房子呢?
1个房子= ( )根
2个房子= ( )根
7个房子= ( )根
n个房子= ( )根
(2)当$n= 99$时,需要多少根小棒?
答案:4.(1)6 11 36 5n + 1
(2)5×99 + 1 = 496(根)
【提示】把n = 99代入。
(2)5×99 + 1 = 496(根)
【提示】把n = 99代入。
5. 一列长120米的火车,以每秒a米的速度通过一座大桥,从车头上桥到车尾离桥共用48秒,这座大桥长多少米?
(1)这座大桥的长度是( )米。(用含有字母的式子表示)
(2)当$a= 15$时,这座大桥长多少米?
(1)这座大桥的长度是( )米。(用含有字母的式子表示)
(2)当$a= 15$时,这座大桥长多少米?
答案:5.(1)48a - 120
(2)当a = 15时,48a - 120 = 48×15 - 120 = 600。
【提示】由题意可知,火车行驶的路程 = 桥长 + 火车车长。
(2)当a = 15时,48a - 120 = 48×15 - 120 = 600。
【提示】由题意可知,火车行驶的路程 = 桥长 + 火车车长。
6. 跨学科心率人在运动时所能承受的心跳速率通常和人的年龄有关。用a表示一个人的年龄,用b表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,则$b= 0.8×(220-a)$。
(1)正常情况下,一个10岁的少年在运动时所能承受的每分钟心跳最高是多少次?
(2)当一个45岁的人在运动时,10秒心跳的次数为30次,他有危险吗?
(1)正常情况下,一个10岁的少年在运动时所能承受的每分钟心跳最高是多少次?
(2)当一个45岁的人在运动时,10秒心跳的次数为30次,他有危险吗?
答案:6.(1)当a = 10时,b = 0.8×(220 - a)=0.8×(220 - 10)=168。
一个10岁的少年在运动时所能承受的每分钟心跳最高是168次。
【提示】将a = 10代入式子计算即可。
(2)当a = 45时,b = 0.8×(220 - a)=0.8×(220 - 45)=140。
30×(60÷10)=180(次)
180 > 140,他有危险。
【提示】根据题意,当a = 45时,b = 0.8×(220 - a)=0.8×(220 - 45)=140,也就是说,一个45岁的人在运动时,他能承受的每分钟心跳的最高次数是140次。如果这个人10秒心跳次数为30次,那么一分钟心跳次数为30×(60÷10)=180(次)。因为180 > 140,所以他有危险。
一个10岁的少年在运动时所能承受的每分钟心跳最高是168次。
【提示】将a = 10代入式子计算即可。
(2)当a = 45时,b = 0.8×(220 - a)=0.8×(220 - 45)=140。
30×(60÷10)=180(次)
180 > 140,他有危险。
【提示】根据题意,当a = 45时,b = 0.8×(220 - a)=0.8×(220 - 45)=140,也就是说,一个45岁的人在运动时,他能承受的每分钟心跳的最高次数是140次。如果这个人10秒心跳次数为30次,那么一分钟心跳次数为30×(60÷10)=180(次)。因为180 > 140,所以他有危险。
附加题。(共10分,不计入总分)
如下图,把同样大的黑色棋子摆放在正多边形的各边上,按照这样的规律摆下去。

(1)第5个图形中的黑色棋子有( )枚。
(2)第n个图形中的黑色棋子有多少枚? (用含有n的式子表示)
如下图,把同样大的黑色棋子摆放在正多边形的各边上,按照这样的规律摆下去。

(1)第5个图形中的黑色棋子有( )枚。
(2)第n个图形中的黑色棋子有多少枚? (用含有n的式子表示)
答案:附加题
(1)35 (2)n(n + 2)枚 【提示】观察发现第1个三角形中的黑色棋子有3枚,可以看成是由“1×3”得到的。第2个正方形中的黑色棋子有8枚,可以看成是由“2×4”得到的。第3个五边形中的黑色棋子有15枚,可以看成是由“3×5”得到的。第4个六边形中的黑色棋子有24枚,可以看成是由“4×6”得到的。则第5个图形中的黑色棋子有5×7 = 35(枚),第n个图形中的黑色棋子有n(n + 2)枚。
(1)35 (2)n(n + 2)枚 【提示】观察发现第1个三角形中的黑色棋子有3枚,可以看成是由“1×3”得到的。第2个正方形中的黑色棋子有8枚,可以看成是由“2×4”得到的。第3个五边形中的黑色棋子有15枚,可以看成是由“3×5”得到的。第4个六边形中的黑色棋子有24枚,可以看成是由“4×6”得到的。则第5个图形中的黑色棋子有5×7 = 35(枚),第n个图形中的黑色棋子有n(n + 2)枚。