2. A、B、C、D、E五名同学一起比赛象棋,每两人都要比赛一盘,到现在,A已经赛了3盘,B已经赛了2盘,C已经赛了1盘,D已经赛了4盘。这时E已经赛了几盘?
答案:
2盘
[提示]五名同学进行象棋比赛,那么每人就要和其他4人下棋,最多下4盘。D已赛了4盘,所以D已经和所有的人都下了一盘;C赛了1盘,是和D下的;A赛了3盘,他没和C下,与其他的3人各下了一盘;B赛了2盘,他就和D、A各下了一盘,没有和E下;所以和E下的只有D和A,即E下了2盘。也可以画图表示,如下:
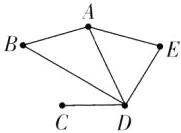
2盘
[提示]五名同学进行象棋比赛,那么每人就要和其他4人下棋,最多下4盘。D已赛了4盘,所以D已经和所有的人都下了一盘;C赛了1盘,是和D下的;A赛了3盘,他没和C下,与其他的3人各下了一盘;B赛了2盘,他就和D、A各下了一盘,没有和E下;所以和E下的只有D和A,即E下了2盘。也可以画图表示,如下:

例3 老师带领五年级一班同学去划船,每条大船可以坐6人,每条小船可以坐4人,每条船都不能有空位,师生共有46人。有几种不同的租船方案?
答案:思路分析
本题既可以从租大船考虑,也可以从租小船考虑。若从租大船考虑,则从租0条大船到租1条、2条、3条、4条、5条、6条、7条、8条大船,可列表整理。
解答:根据题意可列表整理租船方案如表:
从表中可以看出,共有4种租船方案。
本题既可以从租大船考虑,也可以从租小船考虑。若从租大船考虑,则从租0条大船到租1条、2条、3条、4条、5条、6条、7条、8条大船,可列表整理。
解答:根据题意可列表整理租船方案如表:
从表中可以看出,共有4种租船方案。
3. 42名同学准备去公园春游,每辆面包车限载客6人,每辆小汽车限载客4人,不能有空位。有几种不同的乘车方案?
答案:面包车/辆 7 5 3 1
小汽车/辆 0 3 6 9
有4种不同的乘车方案。
[提示]先列出表格,可以从乘面包车考虑,也可以从乘小汽车考虑,但要保证每辆车上都没有空位且人全部要上车,据此可以得到答案。
小汽车/辆 0 3 6 9
有4种不同的乘车方案。
[提示]先列出表格,可以从乘面包车考虑,也可以从乘小汽车考虑,但要保证每辆车上都没有空位且人全部要上车,据此可以得到答案。
例 一堆棋子共62枚,甲、乙两人轮流拿棋子,谁拿到最后1枚谁就获胜,每人每次只能拿1~4枚,不许不拿,甲先拿,乙后拿。请问谁有必胜的把握,他要采取何种策略?
答案:解析:这是一个Nim游戏的一个变体,在这个游戏中,必胜的策略是保持每次轮到对手拿的时候,剩余的棋子数是5的倍数加1。若一开始就是5的倍数加1,则先拿者败。因为这个游戏限制了每次只能拿1~4枚棋子,如果对手拿n枚,你就可以拿$5-n$枚,这样每次两人一共拿走5枚,你就可以控制游戏的节奏。由于$62 \equiv 2 \pmod{5}$,所以甲一开始先拿走2枚,使得剩下的棋子数为5的倍数加1。(在本题中即为60枚,是5的倍数)接下来,无论乙拿走多少枚(1~4枚),甲都可以拿走一定数量的棋子,使得两人一共拿走5枚。这样,甲每次都能确保在每一轮结束后,剩余的棋子数仍然是5的倍数加1。随着游戏的进行,棋子数量逐渐减少,但甲始终能保持必胜状态,直到最后。当只剩下5枚棋子时,无论乙如何拿取(1~4枚),甲都可以在下一轮拿走剩余的棋子,从而获胜。
答案:甲有必胜的把握。甲先拿2枚,乙如果拿1枚,甲就拿4枚;乙如果拿2枚,甲就拿3枚;乙如果拿3枚,甲就拿2枚;乙如果拿4枚,甲就拿1枚。即甲再拿时拿的枚数和乙拿的枚数加起来是5,那么甲一定取到最后1枚而获胜。
答案:甲有必胜的把握。甲先拿2枚,乙如果拿1枚,甲就拿4枚;乙如果拿2枚,甲就拿3枚;乙如果拿3枚,甲就拿2枚;乙如果拿4枚,甲就拿1枚。即甲再拿时拿的枚数和乙拿的枚数加起来是5,那么甲一定取到最后1枚而获胜。
桌子上有300根火柴,允许每人每次取1~6根,不能不取。甲先乙后轮流取火柴,谁取到最后1根火柴就算获胜。谁能获胜?怎样取才能获胜?
答案:甲能获胜,甲可先拿6根,然后再拿时,与乙所拿火柴根数的和是7,才能获胜。
[提示]因为$300÷(1 + 6) = 42$(组)……6(根),所以甲要先拿6根火柴,然后再拿时,都要与乙所拿火柴根数的和是7,如此拿下去,甲将取到最后1根火柴而获胜。
[提示]因为$300÷(1 + 6) = 42$(组)……6(根),所以甲要先拿6根火柴,然后再拿时,都要与乙所拿火柴根数的和是7,如此拿下去,甲将取到最后1根火柴而获胜。