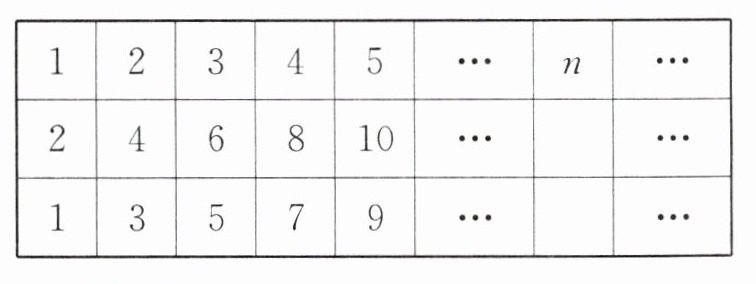
例(教材P104)先找出下表中每行数的排列规律,再用含有字母的式子填空。

答案:思路分析
本题主要考查根据每行数的排列规律,用含有字母的式子来表示相应的数。
对于第一行,是连续的自然数,用字母$n$表示第$n$个数,其规律就是$n$。
对于第二行,是从$2$开始的连续偶数,观察可知第二行的数是第一行对应数的$2$倍,所以第二行第$n$个数可表示为$2n$。
对于第三行,是从$1$开始的连续奇数,观察发现第三行的数是第二行对应的数减去$1$,因为第二行第$n$个数是$2n$,所以第三行第$n$个数可表示为$2n - 1$。
解答
$n$ $2n$ $2n - 1$
本题主要考查根据每行数的排列规律,用含有字母的式子来表示相应的数。
对于第一行,是连续的自然数,用字母$n$表示第$n$个数,其规律就是$n$。
对于第二行,是从$2$开始的连续偶数,观察可知第二行的数是第一行对应数的$2$倍,所以第二行第$n$个数可表示为$2n$。
对于第三行,是从$1$开始的连续奇数,观察发现第三行的数是第二行对应的数减去$1$,因为第二行第$n$个数是$2n$,所以第三行第$n$个数可表示为$2n - 1$。
解答
$n$ $2n$ $2n - 1$
先找出下表中每行数的排列规律,再用含有字母的式子填空。


$n^{2}$
$3n+1$
答案:$n^{2}$ $3n+1$ 【提示】第一行是连续的自然数,第二行的数是第一行对应数的平方,第三行是从4开始连续增加3的数。
解析:
$n^{2}$ $3n+1$
例1 如下图,一个长方形的长是$a$米,宽是$b$米。如果长和宽各增加3米,那么用含有字母的式子表示面积增加了多少平方米。


答案:
思路分析
图中涂色部分表示的是增加的面积,将其分成三部分,编号后列出相应的式子表示面积增加了多少平方米。

解答:①面积:$3×3 = 9$(平方米)
②面积:$b×3 = 3b$(平方米)
③面积:$a×3 = 3a$(平方米)
共增加的面积:$(3a + 3b + 9)$平方米
思路分析
图中涂色部分表示的是增加的面积,将其分成三部分,编号后列出相应的式子表示面积增加了多少平方米。

解答:①面积:$3×3 = 9$(平方米)
②面积:$b×3 = 3b$(平方米)
③面积:$a×3 = 3a$(平方米)
共增加的面积:$(3a + 3b + 9)$平方米
1. 一个长$a$分米、宽$b$分米的长方形。如果长和宽各减少$c$分米,那么用含有字母的式子表示减少了的面积。
答案:$(ac+bc-c^{2})$平方米 【提示】可以画图进行分析,注意计算时是否有重叠部分。