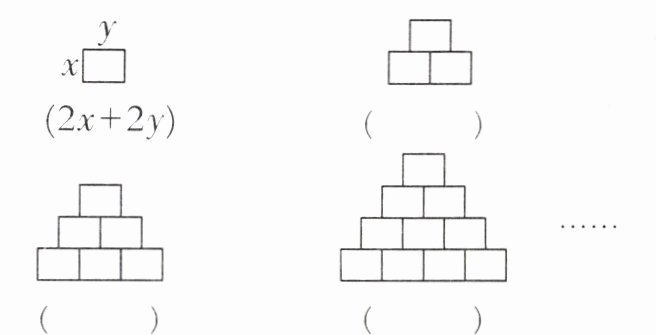
例2 观察下面长方形叠放的规律,用含有字母的式子表示各个图形的周长。
按照这样的方法叠放,第100个图形的周长是

按照这样的方法叠放,第100个图形的周长是
200(x + y)
。答案:解析:第一个图形是一个长方形,长为$y$,宽为$x$,周长公式为$2×(长+宽)$,即$2(x + y)$;
第二个图形是由两个长方形叠放组成,叠放后形成一个长为$2y$,宽为$2x$的大长方形,其周长为$2×(2y + 2x)=4(x + y)$;
第三个图形是由三个长方形叠放组成,叠放后形成一个长为$3y$,宽为$3x$的大长方形,其周长为$2×(3y + 3x)=6(x + y)$;
第四个图形是由四个长方形叠放组成,叠放后形成一个长为$4y$,宽为$4x$的大长方形,其周长为$2×(4y + 4x)=8(x + y)$。
以此类推,第$n$个图形是由$n$个长方形叠放组成,叠放后形成一个长为$ny$,宽为$nx$的大长方形,其周长为$2×(ny + nx)=2n(x + y)$。
当$n = 100$时,第$100$个图形的周长为$2×100(x + y)=200(x + y)$。
答案:$4(x + y)$;$6(x + y)$;$8(x + y)$;第$100$个图形的周长是$200(x + y)$。
第二个图形是由两个长方形叠放组成,叠放后形成一个长为$2y$,宽为$2x$的大长方形,其周长为$2×(2y + 2x)=4(x + y)$;
第三个图形是由三个长方形叠放组成,叠放后形成一个长为$3y$,宽为$3x$的大长方形,其周长为$2×(3y + 3x)=6(x + y)$;
第四个图形是由四个长方形叠放组成,叠放后形成一个长为$4y$,宽为$4x$的大长方形,其周长为$2×(4y + 4x)=8(x + y)$。
以此类推,第$n$个图形是由$n$个长方形叠放组成,叠放后形成一个长为$ny$,宽为$nx$的大长方形,其周长为$2×(ny + nx)=2n(x + y)$。
当$n = 100$时,第$100$个图形的周长为$2×100(x + y)=200(x + y)$。
答案:$4(x + y)$;$6(x + y)$;$8(x + y)$;第$100$个图形的周长是$200(x + y)$。
2. 把若干张长2厘米、宽1厘米的长方形纸片按照下图所示的方式一层层地摆起来。

摆1层,周长是(
像这样继续摆下去,摆$n$层,周长是多少厘米?摆2023层,周长是多少厘米?

摆1层,周长是(
6
)厘米;摆2层,周长是(12
)厘米;摆3层,周长是(18
)厘米。像这样继续摆下去,摆$n$层,周长是多少厘米?摆2023层,周长是多少厘米?
摆n层,周长是$(2×n+1×n)×2=6n$(厘米)。当$n=2023$时,$6n=6×2023=12138$。
答案:6 12 18
摆n层,周长是$(2×n+1×n)×2=6n$(厘米)。当$n=2023$时,$6n=6×2023=12138$。
【提示】分别算出前3个图形的周长,再推出第n个图形的周长。有n个,长就是2n,宽就是n,第n个图形的周长是$(2n+n)×2=6n$;摆2023层,周长是$6×2023=12138$。
摆n层,周长是$(2×n+1×n)×2=6n$(厘米)。当$n=2023$时,$6n=6×2023=12138$。
【提示】分别算出前3个图形的周长,再推出第n个图形的周长。有n个,长就是2n,宽就是n,第n个图形的周长是$(2n+n)×2=6n$;摆2023层,周长是$6×2023=12138$。
例3 如下图,有一个等边三角形,第1次把它分成4个完全相同的小等边三角形,第2次把其中一个小等边三角形继续分成4个更小且完全相同的等边三角形……照这样分下去,第$n$次分完后,三角形共有(

1 + 4n
)个。
答案:解析:本题可通过分析每次分割后三角形个数的变化规律,进而得出第$n$次分完后三角形的总数。
步骤一:分析每次分割后三角形个数的变化情况
原来有$1$个等边三角形。
第$1$次分割:把$1$个等边三角形分成$4$个完全相同的小等边三角形,此时三角形的总数为$1 + 4= 5$个。
第$2$次分割:把其中$1$个小等边三角形继续分成$4$个更小且完全相同的等边三角形,相当于在原来$5$个三角形的基础上又增加了$4$个,此时三角形的总数为$1 + 4 + 4 = 1+4×2 = 9$个。
第$3$次分割:再把其中$1$个小等边三角形分成$4$个更小且完全相同的等边三角形,又增加了$4$个,此时三角形的总数为$1 + 4 + 4 + 4 = 1+4×3 = 13$个。
步骤二:找出规律并得出第$n$次分完后三角形的总数
通过上述分析可以发现,每分一次就增加$4$个三角形,分$n$次就增加$4n$个三角形,再加上原来的$1$个三角形,所以第$n$次分完后,三角形的总数为$(1 + 4n)$个。
答案:$1 + 4n$。
步骤一:分析每次分割后三角形个数的变化情况
原来有$1$个等边三角形。
第$1$次分割:把$1$个等边三角形分成$4$个完全相同的小等边三角形,此时三角形的总数为$1 + 4= 5$个。
第$2$次分割:把其中$1$个小等边三角形继续分成$4$个更小且完全相同的等边三角形,相当于在原来$5$个三角形的基础上又增加了$4$个,此时三角形的总数为$1 + 4 + 4 = 1+4×2 = 9$个。
第$3$次分割:再把其中$1$个小等边三角形分成$4$个更小且完全相同的等边三角形,又增加了$4$个,此时三角形的总数为$1 + 4 + 4 + 4 = 1+4×3 = 13$个。
步骤二:找出规律并得出第$n$次分完后三角形的总数
通过上述分析可以发现,每分一次就增加$4$个三角形,分$n$次就增加$4n$个三角形,再加上原来的$1$个三角形,所以第$n$次分完后,三角形的总数为$(1 + 4n)$个。
答案:$1 + 4n$。
3. 观察下列图形,它是把一个三角形分别连接这个三角形三边的中点,构成4个小三角形,挖去中间的一个小三角形(如图1);对剩下的三个小三角形再分别重复以上做法……将这种做法继续下去(如图2,图3……),则图6中挖去多少个三角形?


答案:364个 【提示】图1挖去中间的1个小三角形,图2挖去中间的$(1+3)$个小三角形,图3挖去中间的$(1+3+3^{2})$个小三角形,则图6挖去中间的$(1+3+3^{2}+3^{3}+3^{4}+3^{5})$个小三角形,即图6挖去中间的364个小三角形。
解析:
图1挖去中间的$1$个小三角形,图2挖去中间的$(1+3)$个小三角形,图3挖去中间的$(1+3+3^{2})$个小三角形,则图6挖去中间的$(1+3+3^{2}+3^{3}+3^{4}+3^{5})$个小三角形。
计算可得:$1+3+3^{2}+3^{3}+3^{4}+3^{5}=1+3+9+27+81+243=364$
364个
计算可得:$1+3+3^{2}+3^{3}+3^{4}+3^{5}=1+3+9+27+81+243=364$
364个