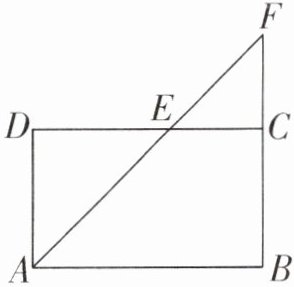
2. 如右下图,四边形ABCD是一个长10厘米、宽6厘米的长方形,三角形ADE的面积比三角形CEF的面积多10平方厘米,求CF的长。

答案:2. 10×6−10=50(平方厘米)
50×2÷10=10(厘米) 10−6=4(厘米)
【提示】由三角形ADE的面积比三角形CEF的面积多10平方厘米,可知三角形ABF的面积比长方形ABCD的面积少10平方厘米,所以三角形ABF的面积为10×6−10=50(平方厘米),即AB×BF÷2=50,所以BF=50×2÷10=10(厘米),故CF=BF−BC=10−6=4(厘米)。
50×2÷10=10(厘米) 10−6=4(厘米)
【提示】由三角形ADE的面积比三角形CEF的面积多10平方厘米,可知三角形ABF的面积比长方形ABCD的面积少10平方厘米,所以三角形ABF的面积为10×6−10=50(平方厘米),即AB×BF÷2=50,所以BF=50×2÷10=10(厘米),故CF=BF−BC=10−6=4(厘米)。
例3(教材P24)下面三个大正方形的边长都是32厘米,先计算每个正方形中小方格的面积,再估计荷叶的面积。


答案:解析:本题考查通过数格子法估计不规则图形的面积,考查点为对不规则图形面积估计方法的理解和运用。解题方法在于先算出每个小方格面积,再分别数出各图中整格数和不满整格数,不满格按半格计算,最后通过公式算出面积并比较。
答案:大正方形的面积:
$32×32 = 1024$(平方厘米)
第一个正方形中每个小方格的面积:
$1024÷16 = 64$(平方厘米)
第二个正方形中每个小方格的面积:
$1024÷64 = 16$(平方厘米)
第三个正方形中每个小方格的面积:
$1024÷256 = 4$(平方厘米)
第一幅图中荷叶面积:
$(4 + 12÷2)×64 = 640$(平方厘米)
第二幅图中荷叶面积:
$(31 + 26÷2)×16 = 704$(平方厘米)
第三幅图中荷叶面积:
$(154 + 52÷2)×4 = 720$(平方厘米)
第三幅图中估计的荷叶面积更接近实际面积,因为第三幅图中分成的小方格更多,在估计时更细致,误差相对更小。
答案:大正方形的面积:
$32×32 = 1024$(平方厘米)
第一个正方形中每个小方格的面积:
$1024÷16 = 64$(平方厘米)
第二个正方形中每个小方格的面积:
$1024÷64 = 16$(平方厘米)
第三个正方形中每个小方格的面积:
$1024÷256 = 4$(平方厘米)
第一幅图中荷叶面积:
$(4 + 12÷2)×64 = 640$(平方厘米)
第二幅图中荷叶面积:
$(31 + 26÷2)×16 = 704$(平方厘米)
第三幅图中荷叶面积:
$(154 + 52÷2)×4 = 720$(平方厘米)
第三幅图中估计的荷叶面积更接近实际面积,因为第三幅图中分成的小方格更多,在估计时更细致,误差相对更小。