例1 如下图,已知长方形ABCD的面积是1200平方厘米,涂色部分的面积是750平方厘米,求四边形EFGO的面积。
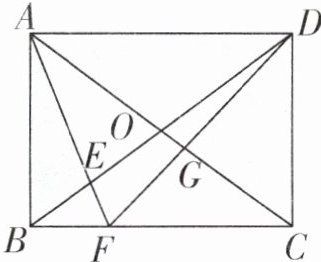

答案:因为长方形ABCD的面积是1200平方厘米,所以三角形ACD的面积为长方形面积的一半,即$1200÷2 = 600$平方厘米。
由思路分析可知,涂色部分的面积等于四边形EFGO的面积加上三角形ACD的面积,所以四边形EFGO的面积 = 涂色部分的面积 - 三角形ACD的面积,即$750 - 600 = 150$平方厘米。
答:四边形EFGO的面积是150平方厘米。
由思路分析可知,涂色部分的面积等于四边形EFGO的面积加上三角形ACD的面积,所以四边形EFGO的面积 = 涂色部分的面积 - 三角形ACD的面积,即$750 - 600 = 150$平方厘米。
答:四边形EFGO的面积是150平方厘米。
1. 如右下图,已知平行四边形ABCD的底是8分米,高是6分米,涂色部分的面积是16平方分米。求四边形EFGH的面积。(G是BD的中点)


答案:1. 16−8×6÷2÷2=4(平方分米)
【提示】因为三角形BAE与三角形CAE同底等高,所以它们的面积相等,若从这两个三角形中同时减去三角形AEF,则剩下的图形面积相等,即三角形ABF与三角形CEF的面积相等,则涂色部分的面积等于四边形EFGH的面积加上三角形DGC的面积。所以要求四边形EFGH的面积,就相当于用图中涂色部分的面积减去三角形DGC的面积。
【提示】因为三角形BAE与三角形CAE同底等高,所以它们的面积相等,若从这两个三角形中同时减去三角形AEF,则剩下的图形面积相等,即三角形ABF与三角形CEF的面积相等,则涂色部分的面积等于四边形EFGH的面积加上三角形DGC的面积。所以要求四边形EFGH的面积,就相当于用图中涂色部分的面积减去三角形DGC的面积。
例2 如下图所示,大直角三角形中的空白部分是一个正方形,求涂色部分的面积。(单位:厘米)


答案:解析:本题主要考查三角形面积的计算。
将涂色部分的两个直角三角形通过旋转和平移,可拼成一个大直角三角形,这个大直角三角形的底是$30$厘米,高是$20$厘米。
根据三角形的面积公式$S = ah÷2$(其中$S$表示面积,$a$表示底,$h$表示高),可得:
$S = 30×20÷2 = 300$(平方厘米)。
答案:涂色部分的面积是$300$平方厘米。
将涂色部分的两个直角三角形通过旋转和平移,可拼成一个大直角三角形,这个大直角三角形的底是$30$厘米,高是$20$厘米。
根据三角形的面积公式$S = ah÷2$(其中$S$表示面积,$a$表示底,$h$表示高),可得:
$S = 30×20÷2 = 300$(平方厘米)。
答案:涂色部分的面积是$300$平方厘米。
2. 右下图直角三角形中的空白部分是正方形,正方形的一个顶点D将这个直角三角形的斜边分成两部分(AD长3厘米),涂色部分的面积是6平方厘米,则DB长多少厘米?


答案:2. 6×2÷3=4(厘米)
【提示】将涂色部分的小三角形绕D点逆时针旋转90°,将两个涂色部分合成一个一条直角边是3厘米、面积是6平方厘米的直角三角形,则另一条直角边为6×2÷3=4(厘米)。
【提示】将涂色部分的小三角形绕D点逆时针旋转90°,将两个涂色部分合成一个一条直角边是3厘米、面积是6平方厘米的直角三角形,则另一条直角边为6×2÷3=4(厘米)。