例3 如下图,把一个组合图形分成三部分,分别用A、B、C表示,求A部分比B部分大多少平方米。(单位:米)
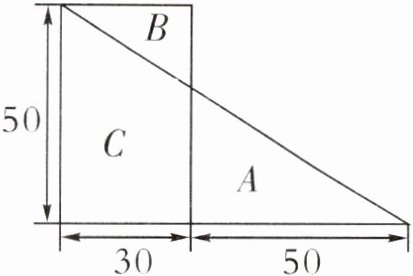

答案:解析:本题考查的知识点是多边形面积的计算及减法中差不变的原理。通过将$A$部分比$B$部分大的面积转化为大三角形($A+C$)和长方形($B+C$)的面积差,利用三角形和长方形面积公式求解。
答案:$(50 + 30)×50÷2-30×50$
$=80×50÷2 - 1500$
$=4000÷2-1500$
$=2000 - 1500$
$= 500$(平方米)
答:$A$部分比$B$部分大$500$平方米。
答案:$(50 + 30)×50÷2-30×50$
$=80×50÷2 - 1500$
$=4000÷2-1500$
$=2000 - 1500$
$= 500$(平方米)
答:$A$部分比$B$部分大$500$平方米。
3. 如图,长方形ABCD中,AB = 8厘米,BC = 6厘米,三角形AFB的面积比三角形FED的面积大12平方厘米,求DE的长度。


答案:3. 8×6−12=36(平方厘米) 36×2÷6−8=4(厘米)
【提示】三角形AFB的面积加上梯形FDCB的面积等于长方形ABCD的面积,三角形FED的面积加上梯形FDCB的面积等于三角形BCE的面积,由条件“三角形AFB的面积比三角形FED的面积大12平方厘米”可知长方形ABCD的面积比三角形BCE的面积大12平方厘米,即三角形BCE的面积=8×6−12=36(平方厘米),可得DE=36×2÷6−8=4(厘米)。
【提示】三角形AFB的面积加上梯形FDCB的面积等于长方形ABCD的面积,三角形FED的面积加上梯形FDCB的面积等于三角形BCE的面积,由条件“三角形AFB的面积比三角形FED的面积大12平方厘米”可知长方形ABCD的面积比三角形BCE的面积大12平方厘米,即三角形BCE的面积=8×6−12=36(平方厘米),可得DE=36×2÷6−8=4(厘米)。
例4 如下图,大、小正方形的边长分别是6厘米与4厘米,求涂色部分的面积。


答案:解析:本题考查了组合图形的面积计算,通过用两个正方形面积和减去空白部分面积得到涂色部分面积。
左边正方形的面积:$6×6 = 36$(平方厘米),
右边正方形的面积:$4×4 = 16$(平方厘米),
左上空白部分的面积:$6×6÷2 = 18$(平方厘米),
右下空白部分的面积:$(6 + 4)×4÷2 = 20$(平方厘米),
右上三角形部分的面积:$(6 - 4)×4÷2 = 4$(平方厘米),
涂色部分的面积:$36 + 16 - (18 + 20) + 4 = 18$(平方厘米)。
答案:涂色部分的面积是18平方厘米。
左边正方形的面积:$6×6 = 36$(平方厘米),
右边正方形的面积:$4×4 = 16$(平方厘米),
左上空白部分的面积:$6×6÷2 = 18$(平方厘米),
右下空白部分的面积:$(6 + 4)×4÷2 = 20$(平方厘米),
右上三角形部分的面积:$(6 - 4)×4÷2 = 4$(平方厘米),
涂色部分的面积:$36 + 16 - (18 + 20) + 4 = 18$(平方厘米)。
答案:涂色部分的面积是18平方厘米。
4. 如右下图,大、小正方形的边长分别是10厘米与8厘米,求涂色部分的面积。


答案:4. 两个正方形的面积和:10×10+8×8=164(平方厘米)
左上空白部分的面积:8×8÷2=32(平方厘米)
涂色部分的面积:164−32−(8+10)×10÷2−(10−8)×10÷2=32(平方厘米)
【提示】可以用两个正方形的面积和减去3个空白三角形的面积,求得涂色部分的面积。
左上空白部分的面积:8×8÷2=32(平方厘米)
涂色部分的面积:164−32−(8+10)×10÷2−(10−8)×10÷2=32(平方厘米)
【提示】可以用两个正方形的面积和减去3个空白三角形的面积,求得涂色部分的面积。
5. 边长分别为3厘米、5厘米、4厘米的三个正方形按照右下图摆放,求涂色部分的面积。


答案:
5. (5−4)×(3+5)÷2=4(平方厘米)
4×4÷2=8(平方厘米) 8+4=12(平方厘米)
【提示】把涂色部分分成两个三角形(如下图)。涂色部分上面的三角形的底是5−4=1(厘米),高是3+5=8(厘米);涂色部分下面的三角形的底和高都是4厘米。这样就可以分别求出每个三角形的面积,进而求出涂色部分的面积。

5. (5−4)×(3+5)÷2=4(平方厘米)
4×4÷2=8(平方厘米) 8+4=12(平方厘米)
【提示】把涂色部分分成两个三角形(如下图)。涂色部分上面的三角形的底是5−4=1(厘米),高是3+5=8(厘米);涂色部分下面的三角形的底和高都是4厘米。这样就可以分别求出每个三角形的面积,进而求出涂色部分的面积。
