例 如下图,已知AD = EC = 4厘米,BD = BE = 6厘米,则图中涂色部分的面积是多少平方厘米?
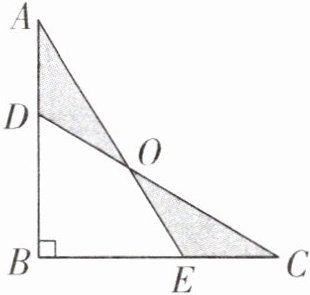

答案:解析:本题主要考查多边形面积的计算,关键利用对称性质得到各部分面积关系。
答案:
三角形$ABE$的面积:$6×(6 + 4)÷2 = 30$(平方厘米)
涂色部分的面积:$30÷(4 + 6 + 6)×4×2 = 15$(平方厘米)
答:图中涂色部分的面积是$15$平方厘米。
答案:
三角形$ABE$的面积:$6×(6 + 4)÷2 = 30$(平方厘米)
涂色部分的面积:$30÷(4 + 6 + 6)×4×2 = 15$(平方厘米)
答:图中涂色部分的面积是$15$平方厘米。
1. 如图,线段BG将一个边长是10分米的正方形分成两个高相等的直角梯形与一个直角三角形,已知线段EF分成的两个梯形面积的差是10平方分米,AF = FD,则图中CG的长是多少分米?


答案:
1. 10×2÷(10÷2)=4(分米) 【提示】如图①,连接CE,易知梯形ABEF和梯形DCEF的面积相等,因为梯形ABEF和梯形DGEF的面积差是10平方分米,所以梯形DCEF和梯形DGEF的面积差也是10平方分米,即三角形GCE的面积是10平方分米,所以CG=10×2÷(10÷2)=4(分米)。

1. 10×2÷(10÷2)=4(分米) 【提示】如图①,连接CE,易知梯形ABEF和梯形DCEF的面积相等,因为梯形ABEF和梯形DGEF的面积差是10平方分米,所以梯形DCEF和梯形DGEF的面积差也是10平方分米,即三角形GCE的面积是10平方分米,所以CG=10×2÷(10÷2)=4(分米)。

2. 如右下图,四边形ABCD是一个正方形,边长是6厘米,E、F分别是CD、BC的中点,求涂色部分的面积。


答案:2. 6×(6÷2)÷2=9(平方厘米)
6×6−9÷3×4=24(平方厘米)
【提示】如图②,连接CG,给空白部分标上序号,则图形关于直线CG对称。则有①的面积=④的面积,②的面积=③的面积。又因为DE=EC,CF=FB,所以①的面积=②的面积=③的面积=④的面积,三角形DCF的面积为6×(6÷2)÷2=9(平方厘米),所以涂色部分的面积为6×6−9÷3×4=24(平方厘米)。
6×6−9÷3×4=24(平方厘米)
【提示】如图②,连接CG,给空白部分标上序号,则图形关于直线CG对称。则有①的面积=④的面积,②的面积=③的面积。又因为DE=EC,CF=FB,所以①的面积=②的面积=③的面积=④的面积,三角形DCF的面积为6×(6÷2)÷2=9(平方厘米),所以涂色部分的面积为6×6−9÷3×4=24(平方厘米)。
3. 如右下图,长方形ABCD的长是8厘米,宽是4厘米,涂色三角形GEC的面积是10平方厘米,求OF的长。


答案:
3. 8×4÷2−10=6(平方厘米) 6×2÷4=3(厘米)
【提示】如下图,连接DE、DO。观察发现,三角形GEO与三角形DEO同底等高,则它们的面积相等。用三角形ECD的面积减去涂色部分的面积,就可以求出三角形OCD的面积,为8×4÷2−10=6(平方厘米)。三角形OCD的底CD的长为4厘米,则它的高OF的长为6×2÷4=3(厘米)。

3. 8×4÷2−10=6(平方厘米) 6×2÷4=3(厘米)
【提示】如下图,连接DE、DO。观察发现,三角形GEO与三角形DEO同底等高,则它们的面积相等。用三角形ECD的面积减去涂色部分的面积,就可以求出三角形OCD的面积,为8×4÷2−10=6(平方厘米)。三角形OCD的底CD的长为4厘米,则它的高OF的长为6×2÷4=3(厘米)。
