1. 化简下面各比。
16:$\frac{1}{2}$
0.8:0.2
1.25:0.5
$\frac{5}{6}:\frac{2}{3}$
$\frac{3}{5}\text{km}:800\text{m}$
15 吨:2750 千克
16:$\frac{1}{2}$
0.8:0.2
1.25:0.5
$\frac{5}{6}:\frac{2}{3}$
$\frac{3}{5}\text{km}:800\text{m}$
15 吨:2750 千克
答案:32:1 4:1 5:2 5:4 3:4 60:11 【提示】根据比的基本性质化简。
解析:
16:$\frac{1}{2}=(16×2):(\frac{1}{2}×2)=32:1$
0.8:0.2=(0.8×10):(0.2×10)=8:2=4:1
1.25:0.5=(1.25×100):(0.5×100)=125:50=5:2
$\frac{5}{6}:\frac{2}{3}=(\frac{5}{6}×6):(\frac{2}{3}×6)=5:4$
$\frac{3}{5}\text{km}:800\text{m}=600\text{m}:800\text{m}=3:4$
15吨:2750千克=15000千克:2750千克=60:11
0.8:0.2=(0.8×10):(0.2×10)=8:2=4:1
1.25:0.5=(1.25×100):(0.5×100)=125:50=5:2
$\frac{5}{6}:\frac{2}{3}=(\frac{5}{6}×6):(\frac{2}{3}×6)=5:4$
$\frac{3}{5}\text{km}:800\text{m}=600\text{m}:800\text{m}=3:4$
15吨:2750千克=15000千克:2750千克=60:11
(1)一根铁丝原来长 6 米,用去了 3.6 米。用去的长度与原来长度的最简单的整数比是
3:5
,剩下的长度与用去的长度的最简单的整数比是2:3
。答案:3:5 2:3 【提示】一根铁丝原来长6米,用去了3.6米。用去的长度与原来长度的比是3.6:6=3:5。把这根铁丝的长度看作5份,则用去了3份,还剩下2份,因此剩下的长度与用去的长度的比是2:3。
解析:
3:5;2:3
(2)从甲地开往乙地,客车要行 10 小时,货车要行 15 小时,客车与货车所用时间的最简单的整数比是(
2:3
),客车与货车速度的最简单的整数比是(3:2
)。答案:2:3 3:2 【提示】客车要行10小时,货车要行15小时,客车与货车所用时间的比是10:15=2:3。把路程看作单位“1”,则客车与货车速度的比是$\frac{1}{10}:\frac{1}{15}=3:2$。
解析:
2:3;3:2
(1)《中华人民共和国国旗法》规定,国旗长与宽的比为$3:2$。以下选项中,不符合标准规格的是(
A.$288\ \text{cm}× 192\ \text{cm}$
B.$96\ \text{cm}× 60\ \text{cm}$
C.$240\ \text{cm}× 160\ \text{cm}$
D.$144\ \text{cm}× 96\ \text{cm}$
B
)。A.$288\ \text{cm}× 192\ \text{cm}$
B.$96\ \text{cm}× 60\ \text{cm}$
C.$240\ \text{cm}× 160\ \text{cm}$
D.$144\ \text{cm}× 96\ \text{cm}$
答案:B 【提示】根据比的意义,分别写出四个选项中两个数的比,看哪个是3:2,是的能作为国旗的尺寸,否则不能作为国旗的尺寸。
(2)新情境 飞船数量 天舟和神舟都是我国自主研发的航天飞船。截至 2024 年 1 月17 日,我国神舟系列飞船数量的$\frac{2}{17}等于天舟系列飞船数量的\frac{2}{7}$,则此时神舟系列与天舟系列飞船数量的最简单的整数比是(
A.$7:17$
B.$17:7$
C.$4:7$
D.$7:4$
B
)。A.$7:17$
B.$17:7$
C.$4:7$
D.$7:4$
答案:B 【提示】设神舟系列飞船的数量为单位“1”,由神舟系列飞船数量的$\frac{2}{17}$等于天舟系列飞船数量的$\frac{2}{7}$,可知天舟系列飞船的数量为$\frac{2}{17}÷\frac{2}{7}=\frac{7}{17}$,神舟系列飞船数量与天舟系列飞船数量的比为$1:\frac{7}{17}=17:7$。
4. 如下图,梯形的上底是 4.5 厘米,下底是8 厘米。

(1)画一条线段,将梯形分成一个平行四边形和一个三角形。
(2)这个三角形与平行四边形面积的最简单的整数比是多少?

(1)画一条线段,将梯形分成一个平行四边形和一个三角形。
(2)这个三角形与平行四边形面积的最简单的整数比是多少?
答案:
(1)画法不唯一,如下图。
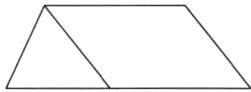
(2)假设梯形的高是a厘米。
平行四边形的面积:$4.5×a=4.5a$(平方厘米)
三角形的面积:$(8-4.5)×a÷2=1.75a$(平方厘米)
$1.75a:4.5a=7:18$
【提示】从题图可看出,平行四边形的底是4.5厘米,三角形的底是$8-4.5=3.5$(厘米),平行四边形和三角形的高都未知,但相等。可以假设高是a厘米,先分别表示出平行四边形和三角形的面积,再算出三角形与平行四边形面积的最简单的整数比。
(1)画法不唯一,如下图。

(2)假设梯形的高是a厘米。
平行四边形的面积:$4.5×a=4.5a$(平方厘米)
三角形的面积:$(8-4.5)×a÷2=1.75a$(平方厘米)
$1.75a:4.5a=7:18$
【提示】从题图可看出,平行四边形的底是4.5厘米,三角形的底是$8-4.5=3.5$(厘米),平行四边形和三角形的高都未知,但相等。可以假设高是a厘米,先分别表示出平行四边形和三角形的面积,再算出三角形与平行四边形面积的最简单的整数比。
5. 把一批零件的加工任务分给师徒两人完成,师父完成了自己任务的$\frac{7}{12}$,徒弟完成了自己任务的$\frac{4}{9}$,这时他们剩下的零件数量一样多。师父和徒弟分到的零件数量的最简单的整数比是多少?
答案:$(1-\frac{4}{9}):(1-\frac{7}{12})=4:3$
【提示】师傅完成了自己任务的$\frac{7}{12}$,则师傅还剩$1-\frac{7}{12}=\frac{5}{12}$;徒弟完成自己任务的$\frac{4}{9}$,则还剩$1-\frac{4}{9}=\frac{5}{9}$。根据“这时他们剩下的零件数量一样多”可知,师父分到的零件数$×\frac{5}{12}=$徒弟分到的零件数$×\frac{5}{9}$。把剩下的零件数量看作单位“1”,则师傅分到的零件数量是$1÷\frac{5}{12}=\frac{12}{5}$,徒弟分到的零件数量是$1÷\frac{5}{9}=\frac{9}{5}$,因此师父分到的零件数:徒弟分到的零件数$=\frac{12}{5}:\frac{9}{5}=4:3$。
【提示】师傅完成了自己任务的$\frac{7}{12}$,则师傅还剩$1-\frac{7}{12}=\frac{5}{12}$;徒弟完成自己任务的$\frac{4}{9}$,则还剩$1-\frac{4}{9}=\frac{5}{9}$。根据“这时他们剩下的零件数量一样多”可知,师父分到的零件数$×\frac{5}{12}=$徒弟分到的零件数$×\frac{5}{9}$。把剩下的零件数量看作单位“1”,则师傅分到的零件数量是$1÷\frac{5}{12}=\frac{12}{5}$,徒弟分到的零件数量是$1÷\frac{5}{9}=\frac{9}{5}$,因此师父分到的零件数:徒弟分到的零件数$=\frac{12}{5}:\frac{9}{5}=4:3$。