(1) 跨学科 水的组成 水是由氢和氧按1:8的质量比化合而成的。在5.4千克的水中,氢的质量占总质量的$\frac{
1
}{9
}$,氢的质量是(0.6
)千克。答案：$\frac{1}{9}$ 0.6 【提示】已知氢和氧的比是1:8,则氢的质量占总质量的$\frac{1}{1+8}$。
解析：
$\frac{1}{9}$；0.6
(2)六(1)班男生人数是女生人数的$\frac{4}{5}$,则男生人数与女生人数的比是
4:5
；女生人数占全班的$\frac{5
}{9
}$；男生人数与全班人数的比是4:9
。答案：4:5 $\frac{5}{9}$ 4:9 【提示】已知男生人数是女生人数的$\frac{4}{5}$，则把男生人数看作4份，女生人数有这样的5份。因此男生人数与女生人数的比是4:5；女生占全班的$\frac{5}{4+5}$；男生人数与全班人数的比是$\frac{4}{4+5}$。
解析：
4:5；$\frac{5}{9}$；4:9
2. 把下面的三角形分成两部分,使它们面积的比是1:3。
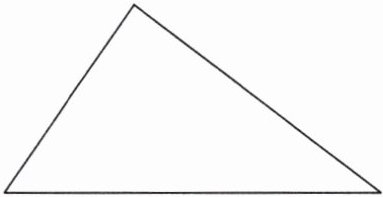
答案：
答案不唯一，如: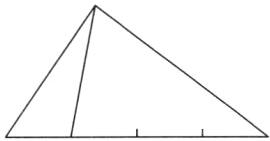
【提示】在高相等的情况下，三角形面积的比就是底的比，可以运用这个规律解决按一定的面积比分三角形的问题。
答案不唯一，如:
【提示】在高相等的情况下，三角形面积的比就是底的比，可以运用这个规律解决按一定的面积比分三角形的问题。(1)一个长方体的棱长之和是64厘米,其中高是2厘米,长与宽的比是4:3。这个长方体的体积是(
A.96
B.100
C.95
D.103
96
)立方厘米。A.96
B.100
C.95
D.103
答案：A 【提示】长+宽+高=64÷4=16(厘米)，长+宽=16 - 2=14(厘米)，长=$14×\frac{4}{4+3}=8$(厘米)，宽=14 - 8=6(厘米)，体积=$8×6×2=96$(立方厘米)。
(2)一块地有$\frac{7}{8}$公顷,其中$\frac{1}{4}$种大豆,$\frac{1}{2}$种棉花,剩下的种玉米,则玉米、大豆、棉花的种植面积之比是(
A.1:1:2
B.2:2:1
C.1:2:1
D.1:2:4
A
)。A.1:1:2
B.2:2:1
C.1:2:1
D.1:2:4
答案：A 【提示】把这块地平均分成4份，则大豆占1份，棉花占2份，玉米占4 - 1 - 2=1(份)。因此玉米、大豆、棉花的种植面积之比是1:1:2。
(3)六(1)班有学生45人,男、女生人数的比可能是(
A.3:7
B.4:5
C.11:3
D.2:9
B
)。A.3:7
B.4:5
C.11:3
D.2:9
答案：B 【提示】每个选项的比的前、后项之和是45的因数才是可能的比，因为男、女生人数必须为整数。
4. 甲、乙、丙、丁四人进行百米比赛,甲的速度比乙快$\frac{2}{5}$,乙的速度比丁慢$\frac{2}{9}$,丙是第一名,谁是第二名？
答案：甲 【提示】乙是中间量。根据甲比乙快$\frac{2}{5}$，可知甲:乙=(5 + 2):5=49:35。根据乙比丁慢$\frac{2}{9}$，可知乙:丁=(9 - 2):9=35:45。则甲:乙:丁=49:35:45。
解析：
设乙的速度为单位“1”。
甲的速度比乙快$\frac{2}{5}$，则甲的速度为$1 + \frac{2}{5} = \frac{7}{5}$，甲:乙$=\frac{7}{5}:1 = 7:5 = 49:35$。
乙的速度比丁慢$\frac{2}{9}$，则乙的速度是丁的$1 - \frac{2}{9} = \frac{7}{9}$，丁的速度为$1÷\frac{7}{9} = \frac{9}{7}$，乙:丁$=1:\frac{9}{7} = 7:9 = 35:45$。
所以甲:乙:丁$=49:35:45$，即甲的速度$=\frac{49}{35}$，丁的速度$=\frac{45}{35}$，比较可得甲的速度大于丁的速度。
已知丙是第一名，所以第二名是甲。
甲
甲的速度比乙快$\frac{2}{5}$，则甲的速度为$1 + \frac{2}{5} = \frac{7}{5}$，甲:乙$=\frac{7}{5}:1 = 7:5 = 49:35$。
乙的速度比丁慢$\frac{2}{9}$，则乙的速度是丁的$1 - \frac{2}{9} = \frac{7}{9}$，丁的速度为$1÷\frac{7}{9} = \frac{9}{7}$，乙:丁$=1:\frac{9}{7} = 7:9 = 35:45$。
所以甲:乙:丁$=49:35:45$，即甲的速度$=\frac{49}{35}$，丁的速度$=\frac{45}{35}$，比较可得甲的速度大于丁的速度。
已知丙是第一名，所以第二名是甲。
甲
5. 实验班原创 应用意识 有若干堆围棋,每堆棋子数一样多,且每堆中白棋子都占$\frac{7}{25}$。小徽从某一堆中拿走一半棋子,且拿走的都是黑棋子,现在所有棋子中,白棋子占$\frac{8}{25}$。一共有多少堆棋子？
答案：假设每堆有棋子100个，那么每堆中白棋子有$100×\frac{7}{25}=28$(个)。设有x堆棋子。$(100x - 100÷2)×\frac{8}{25}=28x$ $x=4$【提示】可假设每堆有棋子100个，根据分数乘法求出每堆中有白棋子的个数。根据题意可知拿走棋子前后，白棋子的数量不变；再设一共有x堆棋子，则拿走50个黑棋子后，白棋子有$[(100x - 100÷2)×\frac{8}{25}]$个，没拿走前白棋子有28x个，再结合上述分析列方程求解即可。
解析：
假设每堆有棋子100个，每堆中白棋子有$100×\frac{7}{25}=28$个。
设有$x$堆棋子。
拿走一半黑棋子后，总棋子数为$100x - 50$，此时白棋子占$\frac{8}{25}$，则白棋子数为$(100x - 50)×\frac{8}{25}$。
因为白棋子数量不变，所以$(100x - 50)×\frac{8}{25}=28x$。
解方程：
$32x - 16 = 28x$
$4x = 16$
$x = 4$
答：一共有4堆棋子。
设有$x$堆棋子。
拿走一半黑棋子后，总棋子数为$100x - 50$，此时白棋子占$\frac{8}{25}$，则白棋子数为$(100x - 50)×\frac{8}{25}$。
因为白棋子数量不变，所以$(100x - 50)×\frac{8}{25}=28x$。
解方程：
$32x - 16 = 28x$
$4x = 16$
$x = 4$
答：一共有4堆棋子。
6. 通往火车站的2号厅有一条人行通道,通道长120米,宽2米。现用边长5分米的正方形地砖铺设。设计人员选用了涂色和白色两种地砖,按箭头方向铺下去,具体铺设方案如下图。
(1)在上图中白色地砖与涂色地砖的面积比是(
(2)铺设这条通道,共需要地砖多少块？其中白色地砖多少块？
(1)在上图中白色地砖与涂色地砖的面积比是(
3:1
)。(2)铺设这条通道,共需要地砖多少块？其中白色地砖多少块？
共需要地砖960块，其中白色地砖720块。
答案：
(1)3:1 【提示】所有涂色地砖都可以平移到最下面一行，这样涂色地砖有1行，白色地砖有3行，因此白色地砖与涂色地砖的面积比是3:1。
(2)5分米=0.5米$(120÷0.5)×(2÷0.5)=960$(块)白色地砖:$960×\frac{3}{3+1}=720$(块)【提示】沿着长需要铺设$120÷0.5=240$(块)地砖，沿着宽需要铺设$2÷0.5=4$(块)地砖，一共需要$240×4=960$(块)地砖。其中白色地砖占$\frac{3}{3+1}$，用“$960×\frac{3}{3+1}$”求出白色地砖有720块。
(1)3:1 【提示】所有涂色地砖都可以平移到最下面一行，这样涂色地砖有1行，白色地砖有3行，因此白色地砖与涂色地砖的面积比是3:1。
(2)5分米=0.5米$(120÷0.5)×(2÷0.5)=960$(块)白色地砖:$960×\frac{3}{3+1}=720$(块)【提示】沿着长需要铺设$120÷0.5=240$(块)地砖，沿着宽需要铺设$2÷0.5=4$(块)地砖，一共需要$240×4=960$(块)地砖。其中白色地砖占$\frac{3}{3+1}$，用“$960×\frac{3}{3+1}$”求出白色地砖有720块。