1. 算一算。
$\frac{5}{12}÷\frac{7}{8}×\frac{21}{4}$
$18×\frac{11}{12}÷\frac{132}{15}$
$\frac{5}{12}÷\frac{7}{8}×\frac{21}{4}$
$18×\frac{11}{12}÷\frac{132}{15}$
答案:$\frac{5}{2}$ $\frac{15}{8}$
解析:
$\frac{5}{12}÷\frac{7}{8}×\frac{21}{4}$
$=\frac{5}{12}×\frac{8}{7}×\frac{21}{4}$
$=\frac{5×8×21}{12×7×4}$
$=\frac{5×(8÷4)×(21÷7)}{12}$
$=\frac{5×2×3}{12}$
$=\frac{30}{12}$
$=\frac{5}{2}$
$18×\frac{11}{12}÷\frac{132}{15}$
$=18×\frac{11}{12}×\frac{15}{132}$
$=\frac{18×11×15}{12×132}$
$=\frac{18×15}{12×12}$
$=\frac{270}{144}$
$=\frac{15}{8}$
$=\frac{5}{12}×\frac{8}{7}×\frac{21}{4}$
$=\frac{5×8×21}{12×7×4}$
$=\frac{5×(8÷4)×(21÷7)}{12}$
$=\frac{5×2×3}{12}$
$=\frac{30}{12}$
$=\frac{5}{2}$
$18×\frac{11}{12}÷\frac{132}{15}$
$=18×\frac{11}{12}×\frac{15}{132}$
$=\frac{18×11×15}{12×132}$
$=\frac{18×15}{12×12}$
$=\frac{270}{144}$
$=\frac{15}{8}$
2. 在○里填“>”“<”或“=”。
$\frac{4}{5}÷4$
$\frac{7}{8}÷\frac{4}{5}$
$\frac{5}{7}÷\frac{10}{7}$
$\frac{5}{3}÷\frac{5}{3}$
$\frac{4}{5}÷4$
<
$\frac{4}{5}$$\frac{7}{8}÷\frac{4}{5}$
>
$\frac{7}{8}$$\frac{5}{7}÷\frac{10}{7}$
<
$\frac{5}{7}$$\frac{5}{3}÷\frac{5}{3}$
=
1答案:< > < = [提示]一个不为0的数除以一个大于1的数,商小于被除数;除以一个大于0小于1的数,商大于被除数;除以它本身,等于1。
解析:
< > < =
3. $5:4= 15÷$(
12
)$=$(25
)$:20= \frac{20}{(16
)}=$(1.25
)(填小数)答案:12 25 16 1.25 [提示]根据比与分数的基本性质填数。
解析:
12 25 16 1.25
(1)如果把$3:7$的前项加上9,要使它的比值不变,那么后项应
A.加上21
B.加上9
C.减去9
D.乘上3
A
。A.加上21
B.加上9
C.减去9
D.乘上3
答案:
(1)A [提示]前项加上9,也就是前项加上3倍,要使它的比值不变,那么后项也应该加上3倍,也就是加上3×7=21,故选A。
(1)A [提示]前项加上9,也就是前项加上3倍,要使它的比值不变,那么后项也应该加上3倍,也就是加上3×7=21,故选A。
(2)传统文化 中药方 东汉名医张仲景的“苓桂术甘汤”药方:茯苓12克,桂枝9克,白术、甘草各6克。王医生按照这个药方配了共重330克的中药,其中茯苓的质量是(
A.120
B.90
C.60
D.$\frac{440}{3}$
120
)克。A.120
B.90
C.60
D.$\frac{440}{3}$
答案:
(2)A [提示]药方中的总质量是12+9+6×2=33(克),其中茯苓占$\frac{12}{33}$。
(2)A [提示]药方中的总质量是12+9+6×2=33(克),其中茯苓占$\frac{12}{33}$。
5. 下面每个小方格的边长表示1厘米。
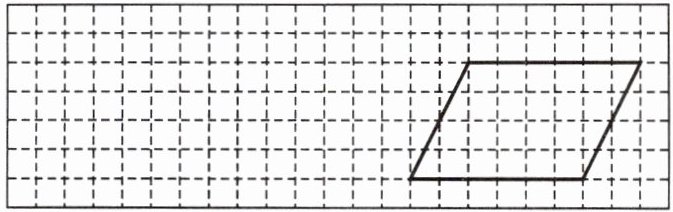
(1)在图中画一个长方形,使长方形的周长是24厘米,长和宽的比是$2:1$。
(2)把右边的平行四边形按$1:2$的面积比分成2份。

(1)在图中画一个长方形,使长方形的周长是24厘米,长和宽的比是$2:1$。
(2)把右边的平行四边形按$1:2$的面积比分成2份。
答案:
(1)长方形如下图。
(2)答案不唯一,如下图。
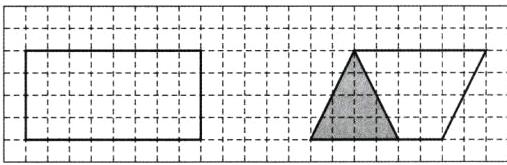
(1)长方形如下图。
(2)答案不唯一,如下图。

6. 新考法 评价说明 一水果店店主用的秤缺斤少两,林华去这家店买2千克苹果,回家一称实际只有1.8千克。于是林华找到店主,店主用店里的秤又称了200克给他。并说:“现在少的都补给你了!”店主说得对吗?
答案:2∶1.8=10∶9 200÷10×9=180(克)
180克=0.18千克
1.98<2,店主说得不对。
[提示]通过计算可以知道,店主称200克,称出的物品实际不足200克。
180克=0.18千克
1.98<2,店主说得不对。
[提示]通过计算可以知道,店主称200克,称出的物品实际不足200克。
7. 若下面三个图形的周长相等,则$a:b:c= $
20∶25∶24
。答案:20∶25∶24 [提示]三个图形的周长分别是6a、4b+a、5c,且它们的周长相等,可得出4b+a=6a,即4b=5a,得出b=$\frac{5}{4}$a,同理得c=$\frac{6}{5}$a。所以a∶b∶c=a∶$\frac{5}{4}$a∶$\frac{6}{5}$a=20∶25∶24。
解析:
三个图形的周长分别是$2×(2a+a)=6a$、$2b+2b+a=4b+a$、$5c$。
因为周长相等,所以$4b+a=6a$,即$4b=5a$,得$b=\frac{5}{4}a$;
同理$5c=6a$,得$c=\frac{6}{5}a$。
则$a:b:c=a:\frac{5}{4}a:\frac{6}{5}a=20:25:24$。
20∶25∶24
因为周长相等,所以$4b+a=6a$,即$4b=5a$,得$b=\frac{5}{4}a$;
同理$5c=6a$,得$c=\frac{6}{5}a$。
则$a:b:c=a:\frac{5}{4}a:\frac{6}{5}a=20:25:24$。
20∶25∶24
8. 原来甲、乙、丙三人共有存款2950元,后来甲取出了450元,乙存入了800元,丙取出了自己存款的$\frac{1}{3}$,现在甲、乙、丙三人存款数之比为$5:3:2$。原来甲、乙、丙三人分别有存款多少元?
答案:2950-450+800=3300(元)
如果丙不取出,那么现在三人的存款数之比为5∶3∶3。
甲:3300×$\frac{5}{5+3+3}$=1500(元)
1500+450=1950(元)
乙:3300×$\frac{3}{5+3+3}$=900(元)
900-800=100(元)
丙:3300×$\frac{3}{5+3+3}$=900(元)
[提示]假设丙不取出存款,则现在甲、乙、丙三人共有存款2950-450+800=3300(元),三人存款数之比为5∶3∶3。把3300元按5∶3∶3进行分配,可求出甲、乙两人现在的存款数和丙原来的存款数,再根据甲取出了450元,乙存入了800元,求出甲、乙两人原来的存款数。
如果丙不取出,那么现在三人的存款数之比为5∶3∶3。
甲:3300×$\frac{5}{5+3+3}$=1500(元)
1500+450=1950(元)
乙:3300×$\frac{3}{5+3+3}$=900(元)
900-800=100(元)
丙:3300×$\frac{3}{5+3+3}$=900(元)
[提示]假设丙不取出存款,则现在甲、乙、丙三人共有存款2950-450+800=3300(元),三人存款数之比为5∶3∶3。把3300元按5∶3∶3进行分配,可求出甲、乙两人现在的存款数和丙原来的存款数,再根据甲取出了450元,乙存入了800元,求出甲、乙两人原来的存款数。