1. 奇妙从一棵树上摘下一些树叶做标本,测量了每片树叶的长与宽。下列说法不正确的是(
A.同一种树叶,长与宽的比值都比较接近
B.长与宽的比值接近的树叶形状相似
C.树叶长与宽的比值越接近1,树叶越狭长
D.树叶长与宽的比值越大,树叶越狭长
C
)。A.同一种树叶,长与宽的比值都比较接近
B.长与宽的比值接近的树叶形状相似
C.树叶长与宽的比值越接近1,树叶越狭长
D.树叶长与宽的比值越大,树叶越狭长
答案:C 【提示】同一种树叶,长与宽的比值比较接近;比值接近的不同树叶,形状也相似;树叶长与宽的比值越接近1,树叶越方正;树叶长与宽的比值越大,树叶越狭长。
2. 新考法 规律探究 星期天,小王和他的伙伴小李、小张、小花、小华来到同一棵大树下,小王、小李和小张每人采集了一片树叶,并分别量出了每片树叶的长和宽,记录在下表中。
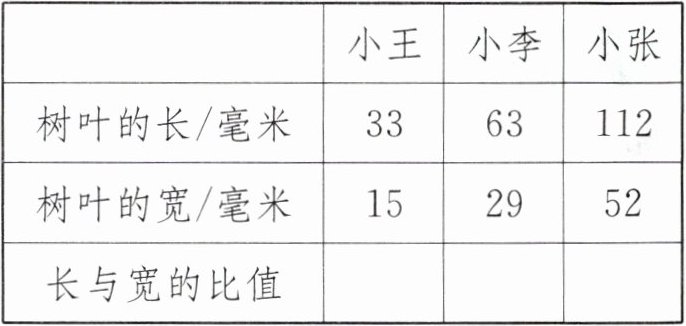
(1)求出每片树叶长与宽的比值(除不尽的得数保留一位小数),填在上表中。
(2)比较每次求得的比值,你有什么发现?
(3)在这棵大树下,小花也采集了一片树叶,它的长是145毫米,宽大约是多少毫米?(结果保留整数)

(1)求出每片树叶长与宽的比值(除不尽的得数保留一位小数),填在上表中。
2.2 2.2 2.2
(2)比较每次求得的比值,你有什么发现?
同一种树叶,长与宽的比值比较接近。
(3)在这棵大树下,小花也采集了一片树叶,它的长是145毫米,宽大约是多少毫米?(结果保留整数)
设宽大约是x毫米。145÷x=2.2,x≈66
答案:
(1)2.2 2.2 2.2
(2)【提示】有的树叶的比值是2.2,有的树叶的比值约是2.2,因此同一种树叶,长与宽的比值比较接近。
(3)设宽大约是x毫米。
145÷x=2.2 x≈66
【提示】根据“长÷宽=2.2”列方程解答。
(1)2.2 2.2 2.2
(2)【提示】有的树叶的比值是2.2,有的树叶的比值约是2.2,因此同一种树叶,长与宽的比值比较接近。
(3)设宽大约是x毫米。
145÷x=2.2 x≈66
【提示】根据“长÷宽=2.2”列方程解答。
3. 小丁在整理柳树、银杏树、枫树和枇杷树这四种树树叶的数据时,忘记在统计表中标出树叶的名称了,他只记得柳树叶最狭长。你能从表格中的数据判断出几号树叶是柳树叶吗?


答案:①30÷55≈0.55 ②232÷87≈2.67
③92÷11≈8.36 ④50÷65≈0.77
8.36>2.67>0.77>0.55,序号③是柳树叶。
【提示】先依次算出每种树叶长与宽的比值,再比较大小,选出比值最大的。
③92÷11≈8.36 ④50÷65≈0.77
8.36>2.67>0.77>0.55,序号③是柳树叶。
【提示】先依次算出每种树叶长与宽的比值,再比较大小,选出比值最大的。
4. 实验班原创 应用意识 某航空母舰的舰长大约是360米,若以模型长度与实际长度的比为1:240制作航空母舰模型,则这个航空母舰模型的舰长是多少米?
答案:360×$\frac{1}{240}$=1.5(米)
【提示】由模型长度与实际长度的比为1:240,可知模型长度是实际长度的$\frac{1}{240}$。
【提示】由模型长度与实际长度的比为1:240,可知模型长度是实际长度的$\frac{1}{240}$。
5. 身高1.8米的小江和弟弟在公园里观赏一尊雕像,他想知道雕像的高度。他灵机一动,站在雕像旁边让弟弟帮他拍摄了一张合影,然后量得照片上他高3厘米,雕像高8厘米,因此他很快算出了雕像的高度。你知道雕像的实际高度是多少米吗?
答案:1.8×$\frac{8}{3}$=4.8(米)
【提示】雕像的实际高度与小江的实际身高的比等于照片中雕像的高度与小江身高的比。由照片上小江高3厘米,雕像高8厘米,可知雕像的高是小江身高的$\frac{8}{3}$。
【提示】雕像的实际高度与小江的实际身高的比等于照片中雕像的高度与小江身高的比。由照片上小江高3厘米,雕像高8厘米,可知雕像的高是小江身高的$\frac{8}{3}$。