1.(扬州江都区·应用意识)《中华人民共和国国旗法》规定了国旗的五种通用规格,宇航员杨利伟在“神舟”五号载人飞船上展示的国旗长15厘米,宽10厘米。四名同学看了这面国旗,提出了自己的想法,(
甲:长是宽的$\frac{3}{2}$。
乙:长比宽长$\frac{1}{2}$。
丙:长与宽的比是$3:2$。
丁:宽比长短$\frac{1}{2}$。
A.甲
B.乙
C.丙
D.丁
D
)的想法是错误的。甲:长是宽的$\frac{3}{2}$。
乙:长比宽长$\frac{1}{2}$。
丙:长与宽的比是$3:2$。
丁:宽比长短$\frac{1}{2}$。
A.甲
B.乙
C.丙
D.丁
答案:D 【提示】根据国旗长15厘米、宽10厘米可知,长是宽的$\frac{3}{2}$,长与宽的比是$3:2$,甲和丙的想法是正确的。根据长与宽的比是$3:2$,可得长比宽长$\frac{1}{2}$,宽比长短$\frac{1}{3}$,因此乙的想法是正确的,丁的想法是错误的。
2.(北京丰台区·应用意识)如右下图,这个正方形被分成了4个部分。其中A和B的面积比是$2:3$,B和C的面积比是$2:1$。如果D的面积是35平方厘米,那么正方形的面积是多少平方厘米?
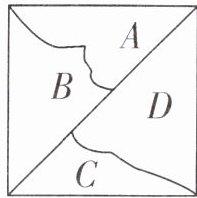

答案:$2:3=4:6$ $2:1=6:3$ $4+6-3=7$(份)A、B、C、D面积的比是$4:6:3:7$。$35÷\frac{7}{4+6+3+7}=100$(平方厘米)【提示】B的面积是中间量,可以把两种表示B的面积的份数转化为相同的份数,即$2:3=4:6$,$2:1=6:3$。因为A与B的面积和等于C与D的面积和,所以D的面积有$4+6-3=7$(份),正方形的面积有$4+6+3+7=20$(份)。最后根据正方形的面积与D的面积关系求出正方形的面积。
解析:
因为A和B的面积比是$2:3$,B和C的面积比是$2:1$,将B的份数统一为6,可得$2:3 = 4:6$,$2:1 = 6:3$,所以A、B、C的面积比为$4:6:3$。
由于正方形被分成4个部分,且A与B的面积和等于C与D的面积和,所以D的面积份数为$4 + 6 - 3=7$份。
A、B、C、D面积的比是$4:6:3:7$,正方形的面积份数为$4 + 6 + 3 + 7=20$份。
已知D的面积是35平方厘米,正方形的面积为$35÷\frac{7}{20}=100$平方厘米。
答案:100
由于正方形被分成4个部分,且A与B的面积和等于C与D的面积和,所以D的面积份数为$4 + 6 - 3=7$份。
A、B、C、D面积的比是$4:6:3:7$,正方形的面积份数为$4 + 6 + 3 + 7=20$份。
已知D的面积是35平方厘米,正方形的面积为$35÷\frac{7}{20}=100$平方厘米。
答案:100
3.(南通市·应用意识)在一杯80克的盐水中,盐与水的质量比是$1:9$,再加入多少克水就能得到盐与水的质量比是$2:23$的盐水?
答案:$80÷(1+9)×1=8$(克)$8÷2×(23+2)=100$(克) $100-80=20$(克)【提示】先求出原来盐水中盐的质量,再根据盐的质量求出稀释后盐水的质量,然后再减去原来盐水的质量,就是需要再加入的水的质量。
解析:
80÷(1+9)×1=8(克)
8÷2×(23+2)=100(克)
100-80=20(克)
答:再加入20克水就能得到盐与水的质量比是2:23的盐水。
8÷2×(23+2)=100(克)
100-80=20(克)
答:再加入20克水就能得到盐与水的质量比是2:23的盐水。
4.(徐州泉山区·量感)早在古代,我们的先辈们就已经掌握了比的知识。如在《九章算术》中有如下描述:粟率五十,粝米三十,稗米二十七,御米二十一,麦四十五,稻六十,豉六十三。译文大致是:古代有一种以粟为基础而定的粮食兑换标准:如果粟的交换率定为50,那么粝米30,稗米27,御米21,麦45,稻60,豉63。比如:50升粟可兑换稻60升。今有粟一斗,欲为粝米,问得几何?译文:现在有粟米1斗(古代1斗约为10升),想换成粝米的话,可以换多少升?
答案:$50:30=5:3$ $10÷5×3=6$(升)【提示】根据题意,先求出粟与粝米的比,再求出10升粟可以换多少升粝米。
解析:
$50:30=5:3$
$10÷5×3=6$(升)
答:可以换6升。
$10÷5×3=6$(升)
答:可以换6升。
5.(淮安市)甲、乙、丙三桶油的质量比是$2:3:4$,如果从乙桶倒出8千克油平均分给甲、丙两桶,那么甲、乙两桶油的质量相等。这三桶油的总质量是多少千克?
答案:$(8+8÷2)÷\left(\frac{3}{2+3+4}-\frac{2}{2+3+4}\right)=108$(千克)【提示】根据题意,甲、乙两桶油的质量分别占总质量的$\frac{2}{2+3+4}$和$\frac{3}{2+3+4}$;甲增加$(8÷2)$千克油,乙倒出8千克油,二者质量相等,则乙比甲多12千克油,用乙比甲多的质量除以对应分率,据此解题即可。方法归纳抓不变量可以把比的问题转化为分数问题,解决这类实际问题时,往往需要抓不变量。把不变量看作单位“1”,再进行计算。
解析:
设这三桶油的总质量是$x$千克。
甲桶油的质量为$\frac{2}{2+3+4}x = \frac{2}{9}x$千克,乙桶油的质量为$\frac{3}{2+3+4}x = \frac{3}{9}x$千克。
从乙桶倒出8千克油平均分给甲、丙两桶后,甲桶油的质量变为$\frac{2}{9}x + 4$千克,乙桶油的质量变为$\frac{3}{9}x - 8$千克。
此时甲、乙两桶油的质量相等,可得方程:
$\frac{3}{9}x - 8 = \frac{2}{9}x + 4$
解得:
$\frac{1}{9}x = 12$
$x = 108$
答:这三桶油的总质量是108千克。
甲桶油的质量为$\frac{2}{2+3+4}x = \frac{2}{9}x$千克,乙桶油的质量为$\frac{3}{2+3+4}x = \frac{3}{9}x$千克。
从乙桶倒出8千克油平均分给甲、丙两桶后,甲桶油的质量变为$\frac{2}{9}x + 4$千克,乙桶油的质量变为$\frac{3}{9}x - 8$千克。
此时甲、乙两桶油的质量相等,可得方程:
$\frac{3}{9}x - 8 = \frac{2}{9}x + 4$
解得:
$\frac{1}{9}x = 12$
$x = 108$
答:这三桶油的总质量是108千克。
6.(连云港市)学校舞蹈队女生人数原来占$\frac{1}{3}$。后来又有6名女生加入,这样女生人数就占舞蹈队总人数$\frac{4}{9}$。原来舞蹈队女生有多少人?
答案:设学校舞蹈队男生有x人。$\left(\frac{4}{9-4}-\frac{1}{3-1}\right)x=6$ $x=20$$1-\frac{1}{3}=\frac{2}{3}$ $20÷\frac{2}{3}=30$(人) $30-20=10$(人)【提示】已知女生人数原来占总人数的$\frac{1}{3}$,则原来的女生人数占男生人数的$\frac{1}{3-1}$;后来又有6名女生加入,这样女生人数就占总人数的$\frac{4}{9}$,则现在女生人数占男生人数的$\frac{4}{9-4}$;由此可以求出6人占男生人数的$\left(\frac{4}{9-4}-\frac{1}{3-1}\right)$,列方程求得男生人数,原来男生人数占舞蹈队总人数的$\left(1-\frac{1}{3}\right)$,用男生人数除以$\left(1-\frac{1}{3}\right)$,求出原来舞蹈队总人数,再减去男生人数,即可求出原来女生有多少人。
解析:
设学校舞蹈队男生有$x$人。
$\left(\frac{4}{9 - 4} - \frac{1}{3 - 1}\right)x = 6$
$\left(\frac{4}{5} - \frac{1}{2}\right)x = 6$
$\frac{3}{10}x = 6$
$x = 20$
$1 - \frac{1}{3} = \frac{2}{3}$
$20 ÷ \frac{2}{3} = 30$(人)
$30 - 20 = 10$(人)
答:原来舞蹈队女生有10人。
$\left(\frac{4}{9 - 4} - \frac{1}{3 - 1}\right)x = 6$
$\left(\frac{4}{5} - \frac{1}{2}\right)x = 6$
$\frac{3}{10}x = 6$
$x = 20$
$1 - \frac{1}{3} = \frac{2}{3}$
$20 ÷ \frac{2}{3} = 30$(人)
$30 - 20 = 10$(人)
答:原来舞蹈队女生有10人。