4. 新情境 黄金比 把一条线段分成两部分,当较短部分与较长部分长度之比等于较长部分与整体长度之比时,我们把这个比称为黄金比(约为$0.618:1$)。当一个物体的两个部分长度的比大致符合黄金比时,常常给人优美的视觉感受,所以,人们设计许多物品时都会考虑黄金比这一因素。
如:图中五角星内线段a的长度与线段b的长度之比符合黄金比$a:b\approx 0.618:1$。
人体健康中的黄金比:人体消化吸收任务的小肠长度与人体的消化道长度之比约为$0.618:1$,消化吸收任务的小肠长度约为5.5米,人体的消化道长度约有多少米?(得数保留整数)
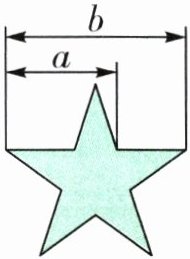
如:图中五角星内线段a的长度与线段b的长度之比符合黄金比$a:b\approx 0.618:1$。
人体健康中的黄金比:人体消化吸收任务的小肠长度与人体的消化道长度之比约为$0.618:1$,消化吸收任务的小肠长度约为5.5米,人体的消化道长度约有多少米?(得数保留整数)

答案:4. $5.5÷0.618≈9$(米)【提示】黄金比是指较短部分与较长部分长度之比等于较长部分与整体长度之比。在这个题目中,我们知道较短部分的长度是5.5米,黄金比约是0.618:1,所以我们可以通过除法来求出整体长度。知识拓展黄金比黄金比,又称黄金分割比,是一个古老而迷人的数学概念,在艺术、建筑、自然界乃至金融领域都有广泛应用。
解析:
5.5÷0.618≈9(米)
5. 新情境 课后服务 课后服务是在“双减”政策背景下推向全国的校园服务,可以在校内提供作业辅导及素质提升课程。实验小学六年级有48人参加课后服务。六年级课后服务开展的是围棋社团和乒乓球社团,其中$\frac {3}{4}$的人参加围棋社团,$\frac {2}{3}$的人参加乒乓球社团。学校规定参加课后服务的每人至少参加一个社团,六年级参加课后服务的人中,两个社团都参加的有多少人?
答案:5. $\frac{3}{4}+\frac{2}{3}-1=\frac{5}{12}$ $48×\frac{5}{12}=20$(人)【提示】每人至少参加一个社团,说明有重叠的分率,先求出两个社团都参加的分率,再求出两个社团都参加的人数。
解析:
$\frac{3}{4}+\frac{2}{3}-1=\frac{9}{12}+\frac{8}{12}-\frac{12}{12}=\frac{5}{12}$
$48×\frac{5}{12}=20$(人)
答:两个社团都参加的有20人。
$48×\frac{5}{12}=20$(人)
答:两个社团都参加的有20人。
6. 甲、乙两个书架上图书本数的比是$3:5$,在乙书架添加5本书后,两个书架上图书本数的比是$1:2$。乙书架原来有图书多少本?
答案:6. 1:2 = 3:6$5÷(6 - 5)×5 = 25$(本)【提示】乙书架添加了5本书,但甲书架上书的本数没有变。将1:2转化为3:6,乙书架上的书由原来的5份变成6份,增加的1份即是5本书,由此可求出乙书架原有的图书本数。
解析:
因为甲书架上书的本数不变,原来甲、乙图书本数比是$3:5$,添加后比是$1:2 = 3:6$。乙书架从$5$份变为$6$份,增加$1$份对应$5$本书,所以乙书架原来有$5÷(6 - 5)×5 = 25$本。
答:乙书架原来有图书$25$本。
答:乙书架原来有图书$25$本。
附加题。(共10分,不计入总分)
小华、小红以同样的速度从A地出发到B地,小华先走120米后,小红才出发;小华到达B地后立即返回,与途中的小红相遇,相遇地点到A地的距离恰好是全程的$\frac {5}{7}$。相遇时小红走了多少米?
小华、小红以同样的速度从A地出发到B地,小华先走120米后,小红才出发;小华到达B地后立即返回,与途中的小红相遇,相遇地点到A地的距离恰好是全程的$\frac {5}{7}$。相遇时小红走了多少米?
答案:附加题 $2-\frac{5}{7}×2=\frac{4}{7}$ $120÷\frac{4}{7}=210$(米)$210×\frac{5}{7}=150$(米)【提示】把全程的长度看作单位“1”。由于速度相同,小华比小红多走了120米,这占全程的$\frac{4}{7}(2-\frac{5}{7}×2)$,求出全程为$120÷\frac{4}{7}=210$(米),则相遇时小红走了$210×\frac{5}{7}=150$(米)。
解析:
把全程看作单位“1”。
相遇时,小红走了全程的$\frac{5}{7}$,小华走了全程的$2 - \frac{5}{7} = \frac{9}{7}$。
小华比小红多走的路程占全程的$\frac{9}{7} - \frac{5}{7} = \frac{4}{7}$。
已知小华比小红多走了120米,所以全程为$120÷\frac{4}{7} = 210$米。
相遇时小红走了$210×\frac{5}{7} = 150$米。
答:相遇时小红走了150米。
相遇时,小红走了全程的$\frac{5}{7}$,小华走了全程的$2 - \frac{5}{7} = \frac{9}{7}$。
小华比小红多走的路程占全程的$\frac{9}{7} - \frac{5}{7} = \frac{4}{7}$。
已知小华比小红多走了120米,所以全程为$120÷\frac{4}{7} = 210$米。
相遇时小红走了$210×\frac{5}{7} = 150$米。
答:相遇时小红走了150米。