1. 公鸡的只数是母鸡的$\frac {1}{8}$,母鸡的只数是公鸡的(
8
)倍。答案:8 【提示】$1÷ \frac{1}{8}=8$
2. 3个羽毛球的质量与1个羽毛球加10克砝码的质量相等,5个乒乓球的质量等于3个羽毛球的质量。一个乒乓球重(
3
)克。答案:3 【提示】根据题意可得2个羽毛球的质量与10克砝码的质量相等,所以1个羽毛球的质量是5克,则一个乒乓球的质量是$5× 3÷ 5=3$(克)。
解析:
3个羽毛球的质量=1个羽毛球的质量+10克,所以2个羽毛球的质量=10克,1个羽毛球的质量=10÷2=5克。5个乒乓球的质量=3个羽毛球的质量=3×5=15克,1个乒乓球的质量=15÷5=3克。
3
3
3. 1支铅笔的价钱相当于1支钢笔的$\frac {1}{6}$,王老师买了4支钢笔和42支铅笔,王老师用去的钱相当于买(
11
)支钢笔的钱或者相当于买(66
)支铅笔的钱。答案:11 66 【提示】因为1支铅笔的价钱相当于1支钢笔的$\frac{1}{6}$,即买一支钢笔的钱可以买6支铅笔,所以王老师买了4支钢笔和42支铅笔,用去的钱相当于买$4+42÷ 6=11$(支)钢笔或者相当于买$42+4× 6=66$(支)铅笔的钱。
解析:
因为1支铅笔的价钱相当于1支钢笔的$\frac{1}{6}$,所以买1支钢笔的钱可以买6支铅笔。
相当于买钢笔的数量:$4 + 42÷6 = 4 + 7 = 11$(支)
相当于买铅笔的数量:$42 + 4×6 = 42 + 24 = 66$(支)
11 66
相当于买钢笔的数量:$4 + 42÷6 = 4 + 7 = 11$(支)
相当于买铅笔的数量:$42 + 4×6 = 42 + 24 = 66$(支)
11 66
4. 一个可乐瓶的容积大约是1.5
升
。把瓶中的可乐全部倒入6个小杯和3个大杯中,正好都倒满。已知每个小杯的容量是每个大杯的$\frac {1}{3}$,若只用大杯,则可以倒满5
个大杯;若只用小杯,则可以倒满15
个小杯。答案:升 5 15 【提示】每个小杯的容量是每个大杯的$\frac{1}{3}$,即1个大杯的容量等于3个小杯的容量,所以6个小杯的容量就等于$6÷ 3=2$(个)大杯的容量,若只用大杯,则可以倒满$3+2=5$(个)大杯。3个大杯的容量就等于$3× 3=9$(个)小杯的容量,若只用小杯,则可以倒满$6+9=15$(个)小杯。
解析:
升 5 15
5. 100位师生绿化校园,老师每人栽3棵树,学生每2人栽1棵树,总共栽了100棵树。老师有(
20
)人,学生有(80
)人。答案:20 80 【提示】由学生每2人栽1棵树,可知学生每人栽$\frac{1}{2}$棵树,假设都是老师,栽树的棵数是$3× 100=300$(棵),比实际栽的多了$300 - 100=200$(棵),每名老师比每名学生多栽$3-\frac{1}{2}=\frac{5}{2}$(棵),则学生的人数是$200÷ \frac{5}{2}=80$(人),老师的人数是$100 - 80=20$(人)。
解析:
假设都是老师,栽树棵数为$3×100 = 300$棵,比实际多$300 - 100 = 200$棵。学生每人栽$\frac{1}{2}$棵,每名老师比学生多栽$3 - \frac{1}{2} = \frac{5}{2}$棵。学生人数为$200÷\frac{5}{2} = 80$人,老师人数为$100 - 80 = 20$人。
20 80
20 80
$2+4= 2×3$ $2+4+6= 3×4$ $2+4+6+8= 4×5$ $2+4+6+8+... +100=$(
50
)×(51
)答案:50 51 【提示】从2开始的连续偶数的和等于:偶数的个数×(偶数的个数+1)。
7. 如下表,小红、小兰和小玲都买了笔记本和钢笔,三人用去的钱一样多。
|物品|小红|小兰|小玲|
|笔记本/本|12|6|9|
|钢笔/支|3|5|?|
(1)1支钢笔的价钱相当于(
(2)小玲买了(
(3)如果每人都用去84元,那么每支钢笔(
|物品|小红|小兰|小玲|
|笔记本/本|12|6|9|
|钢笔/支|3|5|?|
(1)1支钢笔的价钱相当于(
3
)本笔记本的价钱。(2)小玲买了(
4
)支钢笔。(3)如果每人都用去84元,那么每支钢笔(
12
)元。答案:(1)3 【提示】已知他们三人用的钱一样多,小红买了12本笔记本和3支钢笔,小兰买了6本笔记本和5支钢笔,则(5 - 3)支钢笔的钱相当于(12 - 6)本笔记本的钱。
(2)4 【提示】因为1支钢笔的价钱相当于3本笔记本的价钱,小玲比小红少买了(12 - 9)本笔记本,所以小玲买了$3+(12 - 9)÷ 3=4$(支)钢笔。
(3)12 【提示】84元可以买$(3+12÷ 3)$支钢笔,根据“单价=总价÷数量”列式计算。
(2)4 【提示】因为1支钢笔的价钱相当于3本笔记本的价钱,小玲比小红少买了(12 - 9)本笔记本,所以小玲买了$3+(12 - 9)÷ 3=4$(支)钢笔。
(3)12 【提示】84元可以买$(3+12÷ 3)$支钢笔,根据“单价=总价÷数量”列式计算。
8. 学校举办绘画比赛,五、六年级一共创作了120幅水彩画。如果六年级给五年级18幅画,那么两个年级就同样多了。五年级创作了(
42
)幅水彩画,六年级创作了(78
)幅水彩画。答案:42 78 【提示】根据题意可知,六年级比五年级多创作了$(18× 2)$幅,则五年级创作了$(120 - 18× 2)÷ 2=42$(幅),六年级创作了$120 - 42=78$(幅)。
解析:
六年级比五年级多创作的水彩画数量:$18×2=36$(幅)
五年级创作的水彩画数量:$(120 - 36)÷2=42$(幅)
六年级创作的水彩画数量:$120 - 42=78$(幅)
42 78
五年级创作的水彩画数量:$(120 - 36)÷2=42$(幅)
六年级创作的水彩画数量:$120 - 42=78$(幅)
42 78
9. 观察下面三幅图,在装水的杯中放入大球和小球,则1个大球的体积是(
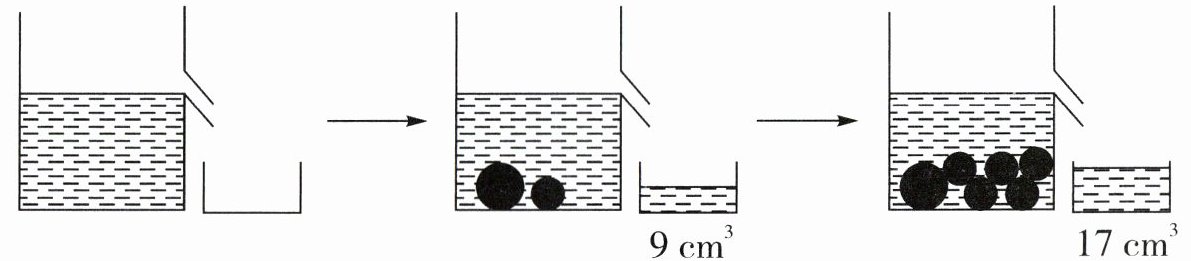
72
)$cm^{3}$,1个小球的体积是(2
)$cm^{3}$。
答案:72 【提示】$(17 - 9)\mathrm{cm}^{3}$相当于4个小球的体积。
解析:
小球体积:$(17-9)÷4=2\,\text{cm}^3$
大球体积:$9-2=7\,\text{cm}^3$
7 2
大球体积:$9-2=7\,\text{cm}^3$
7 2
10. 小刚今年的年龄是爸爸的$\frac {2}{9}$,再过4年,小刚的年龄是爸爸的$\frac {3}{10}$,小刚今年(
8
)岁。答案:8 【提示】因为小刚和爸爸的年龄差不变,所以今年小刚的年龄占年龄差的$\frac{2}{9 - 2}=\frac{2}{7}$,4年后小刚的年龄占年龄差的$\frac{3}{10 - 3}=\frac{3}{7}$,因此4年对应的分率是$\frac{3}{7}-\frac{2}{7}=\frac{1}{7}$,从而可求出小刚和爸爸的年龄差是$4÷ \frac{1}{7}=28$(岁),小刚今年的年龄是$28× \frac{2}{7}=8$(岁)。
1. 下列不属于用假设策略解决问题的是(
A.把接近整十或整百的数看作整十或整百数,估算出大致的结果
B.已知两个数的和与差,先把这两个数看作同样多,再分别求出这两个数
C.把平行四边形沿高剪开后拼成长方形,推导出平行四边形的面积公式
D.计算除数是两位数的除法,先把除数当作整十数来试商
C
)。A.把接近整十或整百的数看作整十或整百数,估算出大致的结果
B.已知两个数的和与差,先把这两个数看作同样多,再分别求出这两个数
C.把平行四边形沿高剪开后拼成长方形,推导出平行四边形的面积公式
D.计算除数是两位数的除法,先把除数当作整十数来试商
答案:C 【提示】选项C运用的是转化策略,不属于假设策略,故选C。