例1(教材P77)一位同学把$(a+\frac {4}{7})×3错当成a+\frac {4}{7}×3$进行计算,这样算出的结果与正确结果相差多少?
思路分析
题目中a是一个未知数,不能直接计算出两道算式的具体结果是多少。解决这道题时,我们可以把两道算式相减,即$(a+\frac {4}{7})×3-(a+\frac {4}{7}×3)$,在计算过程中,要灵活运用乘法分配律和减法的运算性质,从而可得出答案。
解答:$(a+\frac {4}{7})×3-(a+\frac {4}{7}×3)$
$=a×3+\frac {4}{7}×3-a-\frac {4}{7}×3$
$=2a$
答:这样算出的结果与正确结果相差2a。
归纳点拨
整数的运算律对于分数同样适用。熟练运用运算律,可以把复杂问题变简单。
思路分析
题目中a是一个未知数,不能直接计算出两道算式的具体结果是多少。解决这道题时,我们可以把两道算式相减,即$(a+\frac {4}{7})×3-(a+\frac {4}{7}×3)$,在计算过程中,要灵活运用乘法分配律和减法的运算性质,从而可得出答案。
解答:$(a+\frac {4}{7})×3-(a+\frac {4}{7}×3)$
$=a×3+\frac {4}{7}×3-a-\frac {4}{7}×3$
$=2a$
答:这样算出的结果与正确结果相差2a。
归纳点拨
整数的运算律对于分数同样适用。熟练运用运算律,可以把复杂问题变简单。
答案:解析:
本题考查的是分数四则混合运算中运算律的应用。
需要先分别表示出正确结果和错误结果,再计算二者的差值。
正确结果是$(a+\frac {4}{7})×3$,根据乘法分配律,可以将其展开为$3a+\frac {12}{7}$。
错误结果是$a+\frac {4}{7}×3$,计算后得到$a+\frac {12}{7}$。
接着计算二者的差值:
$(3a+\frac {12}{7})-(a+\frac {12}{7})$
$=3a+\frac {12}{7}-a-\frac {12}{7}$
$=2a$
所以,这样算出的结果与正确结果相差$2a$。
答案:
这样算出的结果与正确结果相差$2a$。
本题考查的是分数四则混合运算中运算律的应用。
需要先分别表示出正确结果和错误结果,再计算二者的差值。
正确结果是$(a+\frac {4}{7})×3$,根据乘法分配律,可以将其展开为$3a+\frac {12}{7}$。
错误结果是$a+\frac {4}{7}×3$,计算后得到$a+\frac {12}{7}$。
接着计算二者的差值:
$(3a+\frac {12}{7})-(a+\frac {12}{7})$
$=3a+\frac {12}{7}-a-\frac {12}{7}$
$=2a$
所以,这样算出的结果与正确结果相差$2a$。
答案:
这样算出的结果与正确结果相差$2a$。
1. 小马虎在计算$(a+\frac {5}{36})×3$时,错误地算成$a+\frac {5}{36}×3$,他的结果与正确结果相差多少?
答案:$(a+\frac{5}{36})×3-(a+\frac{5}{36}×3)=3a+\frac{5}{36}×3-a-\frac{5}{36}×3=2a$
[提示]把两道算式相减作差即可。
[提示]把两道算式相减作差即可。
2. 明明在计算$\frac {3}{7}×(\frac {5}{6}-☆)$时,由于把括号抄丢了,所以算出来的结果比正确结果小$\frac {1}{2}$。☆所表示的数是多少?
答案:$\frac{3}{7}×(\frac{5}{6}-☆)-(\frac{3}{7}×\frac{5}{6}-☆)=\frac{3}{7}×\frac{5}{6}-\frac{3}{7}☆-\frac{3}{7}×\frac{5}{6}+☆=\frac{4}{7}☆$
$\frac{4}{7}☆=\frac{1}{2}$,$☆=\frac{1}{2}÷\frac{4}{7}=\frac{7}{8}$
[提示] $\frac{3}{7}×(\frac{5}{6}-☆)$抄丢括号就是$\frac{3}{7}×\frac{5}{6}-☆$,用$\frac{3}{7}×(\frac{5}{6}-☆)$减去$(\frac{3}{7}×\frac{5}{6}-☆)$,差是$\frac{1}{2}$,由此得出只含有☆的方程,根据解方程的方法求解即可。
$\frac{4}{7}☆=\frac{1}{2}$,$☆=\frac{1}{2}÷\frac{4}{7}=\frac{7}{8}$
[提示] $\frac{3}{7}×(\frac{5}{6}-☆)$抄丢括号就是$\frac{3}{7}×\frac{5}{6}-☆$,用$\frac{3}{7}×(\frac{5}{6}-☆)$减去$(\frac{3}{7}×\frac{5}{6}-☆)$,差是$\frac{1}{2}$,由此得出只含有☆的方程,根据解方程的方法求解即可。
3. 安安在计算$\frac {2}{5}×(\frac {5}{8}+△)$时,因为把括号抄丢了,所以算出来的结果与正确结果相差$\frac {3}{20}$。△所表示的数是多少?
答案:$\frac{2}{5}×\frac{5}{8}+△-\frac{2}{5}×(\frac{5}{8}+△)=△-\frac{2}{5}△=\frac{3}{5}△$
$\frac{3}{5}△=\frac{3}{20}$
$△=\frac{3}{20}÷\frac{3}{5}=\frac{1}{4}$
[提示] $\frac{2}{5}×(\frac{5}{8}+△)$抄丢括号就是$\frac{2}{5}×\frac{5}{8}+△$,用$\frac{2}{5}×\frac{5}{8}+△$减去$\frac{2}{5}×(\frac{5}{8}+△)$,差是$\frac{3}{20}$,由此得出只含有△的方程,根据解方程的方法求解即可。
$\frac{3}{5}△=\frac{3}{20}$
$△=\frac{3}{20}÷\frac{3}{5}=\frac{1}{4}$
[提示] $\frac{2}{5}×(\frac{5}{8}+△)$抄丢括号就是$\frac{2}{5}×\frac{5}{8}+△$,用$\frac{2}{5}×\frac{5}{8}+△$减去$\frac{2}{5}×(\frac{5}{8}+△)$,差是$\frac{3}{20}$,由此得出只含有△的方程,根据解方程的方法求解即可。
例2(教材P83)六年级一班有48人,其中$\frac {2}{3}$喜欢跳舞,$\frac {3}{4}$喜欢唱歌,没有人既不喜欢跳舞又不喜欢唱歌。既喜欢跳舞又喜欢唱歌的有多少人?
思路分析
根据“没有人既不喜欢跳舞又不喜欢唱歌”,可以把喜欢跳舞、喜欢唱歌和既喜欢跳舞又喜欢唱歌的用下图表示。
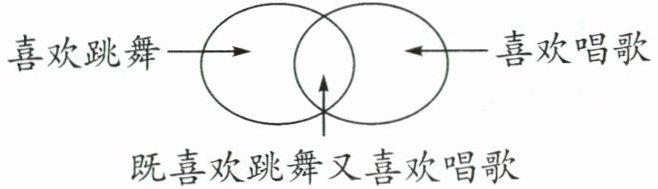
从图中可以看出,既喜欢跳舞又喜欢唱歌的是喜欢跳舞和喜欢唱歌的重叠部分。把喜欢跳舞和喜欢唱歌的人数相加再减去全班人数,就可以算出既喜欢跳舞又喜欢唱歌的人数。
解答:方法一:$48×\frac {2}{3}+48×\frac {3}{4}-48$
$=32+36-48$
$=20$(人)
方法二:$48×(\frac {2}{3}+\frac {3}{4}-1)$
$=48×\frac {5}{12}$
$=20$(人)
答:既喜欢跳舞又喜欢唱歌的有20人。
归纳点拨
借助图形解决复杂的分数问题,能很快地理清数量关系,从而顺利解决问题。
思路分析
根据“没有人既不喜欢跳舞又不喜欢唱歌”,可以把喜欢跳舞、喜欢唱歌和既喜欢跳舞又喜欢唱歌的用下图表示。

从图中可以看出,既喜欢跳舞又喜欢唱歌的是喜欢跳舞和喜欢唱歌的重叠部分。把喜欢跳舞和喜欢唱歌的人数相加再减去全班人数,就可以算出既喜欢跳舞又喜欢唱歌的人数。
解答:方法一:$48×\frac {2}{3}+48×\frac {3}{4}-48$
$=32+36-48$
$=20$(人)
方法二:$48×(\frac {2}{3}+\frac {3}{4}-1)$
$=48×\frac {5}{12}$
$=20$(人)
答:既喜欢跳舞又喜欢唱歌的有20人。
归纳点拨
借助图形解决复杂的分数问题,能很快地理清数量关系,从而顺利解决问题。
答案:喜欢跳舞的人数:
$48×\frac{2}{3}=32$(人),
喜欢唱歌的人数:
$48×\frac{3}{4}=36$(人),
由于没有人既不喜欢跳舞又不喜欢唱歌,所以:
既喜欢跳舞又喜欢唱歌的人数$=32+36-48=20$(人),
另一种思路是直接计算重叠部分:
既喜欢跳舞又喜欢唱歌的人数:
$48×(\frac{2}{3}+\frac{3}{4}-1)$
$=48×\frac{5}{12}$
$=20$(人)
所以既喜欢跳舞又喜欢唱歌的有20人。
$48×\frac{2}{3}=32$(人),
喜欢唱歌的人数:
$48×\frac{3}{4}=36$(人),
由于没有人既不喜欢跳舞又不喜欢唱歌,所以:
既喜欢跳舞又喜欢唱歌的人数$=32+36-48=20$(人),
另一种思路是直接计算重叠部分:
既喜欢跳舞又喜欢唱歌的人数:
$48×(\frac{2}{3}+\frac{3}{4}-1)$
$=48×\frac{5}{12}$
$=20$(人)
所以既喜欢跳舞又喜欢唱歌的有20人。