4. 甲、乙两车分别从A、B两地出发相向而行,甲车行了全程的$\frac {2}{5}$,乙车行了全程的$\frac {3}{4}$,两车相距60千米。求A、B两地之间的距离。
答案:$60÷(\frac{2}{5}+\frac{3}{4}-1)=400$(千米)
[提示]因为两车行驶的总路程超过了全程,所以它们是相遇后再次相距60千米。
[提示]因为两车行驶的总路程超过了全程,所以它们是相遇后再次相距60千米。
5. 六年级有260人,喜欢语文与不喜欢语文的人数比是$8:5$,喜欢数学与不喜欢数学的人数比是$7:6$,两门学科都喜欢的有84人,两门学科都不喜欢的有多少人?
答案:$260×\frac{7}{7+6}-84=56$(人)
$260×\frac{5}{8+5}-56=44$(人)
[提示]喜欢数学的有$260×\frac{7}{7+6}=140$ (人),其中两门学科都喜欢的有84人,这样求出只喜欢数学不喜欢语文的有$140 - 84 = 56$ (人),不喜欢语文的有$260×\frac{5}{8+5}=100$ (人),所以两门学科都不喜欢的就有$100 - 56 = 44$ (人)。
$260×\frac{5}{8+5}-56=44$(人)
[提示]喜欢数学的有$260×\frac{7}{7+6}=140$ (人),其中两门学科都喜欢的有84人,这样求出只喜欢数学不喜欢语文的有$140 - 84 = 56$ (人),不喜欢语文的有$260×\frac{5}{8+5}=100$ (人),所以两门学科都不喜欢的就有$100 - 56 = 44$ (人)。
6. 某校六年级有96名学生,在调查他们会下象棋和围棋的人数时发现,有24名学生两样都不会,有$\frac {1}{8}$的学生两样都会,有$\frac {7}{12}$的学生会下象棋。会下围棋的有多少名学生?
答案:
$96 - 24 - 96×\frac{7}{12}+96×\frac{1}{8}=28$(名)
[提示]两样中至少会下一样的有$96 - 24 = 72$ (名),会下象棋的学生有$96×\frac{7}{12}=56$ (名),会下围棋也会下象棋的学生有$96×\frac{1}{8}=12$ (名),如下图:
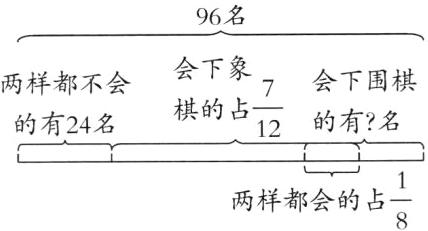
因此两样中至少会下一样的学生人数减去会下象棋的学生人数,还要加上两样都会的学生人数才是会下围棋的学生人数。
$96 - 24 - 96×\frac{7}{12}+96×\frac{1}{8}=28$(名)
[提示]两样中至少会下一样的有$96 - 24 = 72$ (名),会下象棋的学生有$96×\frac{7}{12}=56$ (名),会下围棋也会下象棋的学生有$96×\frac{1}{8}=12$ (名),如下图:

因此两样中至少会下一样的学生人数减去会下象棋的学生人数,还要加上两样都会的学生人数才是会下围棋的学生人数。
例1计算:$(1+\frac {1}{2}+\frac {1}{3}+\frac {1}{4})×(\frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5})-(1+\frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5})×(\frac {1}{2}+\frac {1}{3}+\frac {1}{4})$
思路分析
这道题如果通过通分计算,那么太麻烦了。观察题目中各式的特点,可以用整体替换的方法,设$A= \frac {1}{2}+\frac {1}{3}+\frac {1}{4},B= \frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5}$,这样就可以简便计算了。
解答:设$A= \frac {1}{2}+\frac {1}{3}+\frac {1}{4},B= \frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5}$。
$(1+\frac {1}{2}+\frac {1}{3}+\frac {1}{4})×(\frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5})-$
$(1+\frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5})×(\frac {1}{2}+\frac {1}{3}+\frac {1}{4})$
$=(1+A)×B-(1+B)×A$
$=B+AB-A-AB$
$=B-A$
$=\frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5}-(\frac {1}{2}+\frac {1}{3}+\frac {1}{4})$
$=\frac {1}{5}$
归纳点拨
有些计算题看起来用一般的方法计算很复杂,如果掌握了算式的特点,运用一些特殊的技巧,就可以使计算变得简便。
思路分析
这道题如果通过通分计算,那么太麻烦了。观察题目中各式的特点,可以用整体替换的方法,设$A= \frac {1}{2}+\frac {1}{3}+\frac {1}{4},B= \frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5}$,这样就可以简便计算了。
解答:设$A= \frac {1}{2}+\frac {1}{3}+\frac {1}{4},B= \frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5}$。
$(1+\frac {1}{2}+\frac {1}{3}+\frac {1}{4})×(\frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5})-$
$(1+\frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5})×(\frac {1}{2}+\frac {1}{3}+\frac {1}{4})$
$=(1+A)×B-(1+B)×A$
$=B+AB-A-AB$
$=B-A$
$=\frac {1}{2}+\frac {1}{3}+\frac {1}{4}+\frac {1}{5}-(\frac {1}{2}+\frac {1}{3}+\frac {1}{4})$
$=\frac {1}{5}$
归纳点拨
有些计算题看起来用一般的方法计算很复杂,如果掌握了算式的特点,运用一些特殊的技巧,就可以使计算变得简便。
答案:设 $A = \frac{1}{2} + \frac{1}{3} + \frac{1}{4}$,$B = \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5}$。
$(1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4}) × (\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5}) - (1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5}) × (\frac{1}{2} + \frac{1}{3} + \frac{1}{4})$
$= (1 + A) × B - (1 + B) × A$
$= B + AB - A - AB$
$= B - A$
$= \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} - (\frac{1}{2} + \frac{1}{3} + \frac{1}{4})$
$= \frac{1}{5}$
$(1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4}) × (\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5}) - (1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5}) × (\frac{1}{2} + \frac{1}{3} + \frac{1}{4})$
$= (1 + A) × B - (1 + B) × A$
$= B + AB - A - AB$
$= B - A$
$= \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} - (\frac{1}{2} + \frac{1}{3} + \frac{1}{4})$
$= \frac{1}{5}$