1. (2024·河南)如图,数轴上点 $ P $ 表示的数是 (
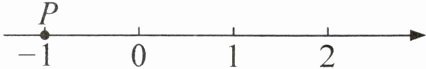
A.$ -1 $
B.$ 0 $
C.$ 1 $
D.$ 2 $
A
)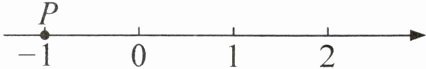
A.$ -1 $
B.$ 0 $
C.$ 1 $
D.$ 2 $
答案:【解析】:本题可根据数轴的定义和特点来确定点$P$所表示的数。
数轴是规定了原点、正方向和单位长度的直线,原点表示的数是$0$,原点右边的点表示正数,原点左边的点表示负数。
观察所给数轴可知,原点为$0$,点$P$在原点左侧且距离原点$1$个单位长度,根据数轴的性质,原点左侧的点表示的数为负数,距离原点$1$个单位长度的负数就是$-1$,所以点$P$表示的数是$-1$。
【答案】:A
数轴是规定了原点、正方向和单位长度的直线,原点表示的数是$0$,原点右边的点表示正数,原点左边的点表示负数。
观察所给数轴可知,原点为$0$,点$P$在原点左侧且距离原点$1$个单位长度,根据数轴的性质,原点左侧的点表示的数为负数,距离原点$1$个单位长度的负数就是$-1$,所以点$P$表示的数是$-1$。
【答案】:A
2. 数轴上点 $ A $ 表示的数是 $ -3 $,将点 $ A $ 在数轴上移动 $ 7 $ 个单位长度得到点 $ B $,则点 $ B $ 表示的数是 (
A.$ 4 $
B.$ -4 $ 或 $ 10 $
C.$ -10 $
D.$ 4 $ 或 $ -10 $
D
)A.$ 4 $
B.$ -4 $ 或 $ 10 $
C.$ -10 $
D.$ 4 $ 或 $ -10 $
答案:【解析】:
本题主要考查数轴上点的移动规律。在数轴上,点向右移动表示的数会增加,点向左移动表示的数会减少。
题目中给出点A表示的数是-3,然后将点A在数轴上移动7个单位长度得到点B。这里需要考虑两种情况:
1. 点A向右移动7个单位长度,那么点B表示的数为$-3 + 7 = 4$。
2. 点A向左移动7个单位长度,那么点B表示的数为$-3 - 7 = -10$。
综合以上两种情况,点B表示的数是4或-10。
【答案】:
D. $4$ 或 $-10$
本题主要考查数轴上点的移动规律。在数轴上,点向右移动表示的数会增加,点向左移动表示的数会减少。
题目中给出点A表示的数是-3,然后将点A在数轴上移动7个单位长度得到点B。这里需要考虑两种情况:
1. 点A向右移动7个单位长度,那么点B表示的数为$-3 + 7 = 4$。
2. 点A向左移动7个单位长度,那么点B表示的数为$-3 - 7 = -10$。
综合以上两种情况,点B表示的数是4或-10。
【答案】:
D. $4$ 或 $-10$
3. 数轴上与原点相距 $ 1.5 $ 个单位长度的点表示的数为
$\pm 1.5$
。答案:【解析】:
本题考查数轴的基本概念。在数轴上,一个点与原点的距离表示该点对应的数的绝对值。题目要求找到与原点相距$1.5$个单位长度的点,即需要找到绝对值为$1.5$的数。
设该点表示的数为$x$,则有$|x| = 1.5$。
解这个方程,我们得到两个$x = 1.5$ 或 $x = -1.5$。
因此,数轴上与原点相距$1.5$个单位长度的点表示的数有两个,分别是$1.5$和$-1.5$。
【答案】:
$\pm 1.5$
本题考查数轴的基本概念。在数轴上,一个点与原点的距离表示该点对应的数的绝对值。题目要求找到与原点相距$1.5$个单位长度的点,即需要找到绝对值为$1.5$的数。
设该点表示的数为$x$,则有$|x| = 1.5$。
解这个方程,我们得到两个$x = 1.5$ 或 $x = -1.5$。
因此,数轴上与原点相距$1.5$个单位长度的点表示的数有两个,分别是$1.5$和$-1.5$。
【答案】:
$\pm 1.5$
4. 在数轴上,$ A $,$ B $ 两点分别表示数 $ -4 $,$ 0 $。将点 $ A $ 向左移动 $ 3 $ 个单位长度,得到的点表示的数是
$-7$
;将点 $ B $ 先向右移动 $ 2 $ 个单位长度,再向左移动 $ 6.5 $ 个单位长度,得到的点表示的数是$-4.5$
。答案:【解析】:
本题主要考查数轴上点的移动规律。在数轴上,点向左移动表示的数会减小,点向右移动表示的数会增大。移动的单位长度就是数的变化量。
对于点A,其初始位置表示的数是-4,向左移动3个单位长度,根据移动规律,新的位置表示的数为$-4 - 3 = -7$。
对于点B,其初始位置表示的数是0,先向右移动2个单位长度,表示的数变为$0 + 2 = 2$,再向左移动6.5个单位长度,表示的数变为$2 - 6.5 = -4.5$。
【答案】:
$-7$;$-4.5$
本题主要考查数轴上点的移动规律。在数轴上,点向左移动表示的数会减小,点向右移动表示的数会增大。移动的单位长度就是数的变化量。
对于点A,其初始位置表示的数是-4,向左移动3个单位长度,根据移动规律,新的位置表示的数为$-4 - 3 = -7$。
对于点B,其初始位置表示的数是0,先向右移动2个单位长度,表示的数变为$0 + 2 = 2$,再向左移动6.5个单位长度,表示的数变为$2 - 6.5 = -4.5$。
【答案】:
$-7$;$-4.5$
5. 若数轴上表示 $ -2025 $ 和 $ 2025 $ 的两点之间共有 $ n $ 个表示整数的点(包括表示 $ -2025 $ 和 $ 2025 $ 的点),则 $ n $ 的值为______
4051
。答案:解:数轴上表示-2025和2025的两点之间的整数点包括-2025,-2024,…,0,…,2024,2025。
从-2025到-1共有2025个整数,从1到2025共有2025个整数,再加上0这1个整数,
所以总个数n=2025+2025+1=4051。
答案:4051
从-2025到-1共有2025个整数,从1到2025共有2025个整数,再加上0这1个整数,
所以总个数n=2025+2025+1=4051。
答案:4051
6. (教材 $ P17 $ 练习 $ 2 $ 变式)在数轴上分别表示下列各数:$ 0 $,$ -4.2 $,$ 3\frac{1}{2} $,$ -2 $,$ +5 $,$ 1\frac{1}{3} $。


答案:【解析】:
题目考查数轴的概念,需要将在给定数轴上准确表示出各数,包括$0$,负数,正数以及分数,根据数轴上点的位置确定数的大小关系,正数在原点右侧,负数在原点左侧,数的大小由其在数轴上的位置决定,越向右越大,越向左越小。
【答案】:
解:
在数轴上,首先找到原点$0$,
对于负数$-4.2$和$-2$,分别向左移动$4.2$个单位和$2$个单位,标记这两个点,
对于正数$3\frac{1}{2}$(即$3.5$)和$+5$,分别向右移动$3.5$个单位和$5$个单位,标记这两个点,
对于分数$1\frac{1}{3}$(即$\frac{4}{3}$,约等于$1.3333$),向右移动大约$1.3333$个单位,标记这个点,
图略。
题目考查数轴的概念,需要将在给定数轴上准确表示出各数,包括$0$,负数,正数以及分数,根据数轴上点的位置确定数的大小关系,正数在原点右侧,负数在原点左侧,数的大小由其在数轴上的位置决定,越向右越大,越向左越小。
【答案】:
解:
在数轴上,首先找到原点$0$,
对于负数$-4.2$和$-2$,分别向左移动$4.2$个单位和$2$个单位,标记这两个点,
对于正数$3\frac{1}{2}$(即$3.5$)和$+5$,分别向右移动$3.5$个单位和$5$个单位,标记这两个点,
对于分数$1\frac{1}{3}$(即$\frac{4}{3}$,约等于$1.3333$),向右移动大约$1.3333$个单位,标记这个点,
图略。
7. 新趋势 情境素材 小明早晨跑步,他从自己家出发,向东跑了 $ 2 \mathrm{km} $ 到达小彬家,继续向东跑了 $ 1.5 \mathrm{km} $ 到达小红家,然后又向西跑了 $ 4.5 \mathrm{km} $ 到达学校,最后又向东跑回到自己家。
(1) 在下面的数轴上,以小明家为原点,向东为正方向,用 $ 1 $ 个单位长度表示 $ 1 \mathrm{km} $,分别用点 $ A $,$ B $,$ C $ 表示出小彬家、小红家和学校的位置;

(2) 求小彬家与学校之间的距离;
(3) 若小明跑步的速度为 $ 250 \mathrm{m/min} $,则小明跑步一共用了多长时间?
(1) 在下面的数轴上,以小明家为原点,向东为正方向,用 $ 1 $ 个单位长度表示 $ 1 \mathrm{km} $,分别用点 $ A $,$ B $,$ C $ 表示出小彬家、小红家和学校的位置;

(2) 求小彬家与学校之间的距离;
(3) 若小明跑步的速度为 $ 250 \mathrm{m/min} $,则小明跑步一共用了多长时间?
答案:【解析】:
(1)根据题意,小明从家出发,先向东跑了2km到达小彬家,即点A,位置在数轴上的2处;
继续向东跑了1.5km到达小红家,即点B,位置在数轴上的$2+1.5=3.5$处;
然后又向西跑了4.5km到达学校,即点C,位置在数轴上的$3.5 - 4.5 = -1$处;
最后又向东跑回到自己家,即原点0。
在数轴上标出这些点,得到:
A点在2的位置,B点在3.5的位置,C点在-1的位置。
数轴图略。
(2)小彬家与学校之间的距离是数轴上点A与点C之间的距离,即$|2 - (-1)| = 3(km)$。
(3)小明跑步的总路程是各段路程的绝对值之和,
即$|2| + |1.5| + |-4.5| + |-1-0| = 2 + 1.5 + 4.5 + 1 = 9(km)$。
换算成米,即$9km = 9000m$。
根据速度等于路程除以时间的公式,时间$t = \frac{9000}{250} = 36(min)$。
【答案】:
(1)数轴图略;
(2)小彬家与学校之间的距离是$3km$;
(3)小明跑步一共用了$36min$。
(1)根据题意,小明从家出发,先向东跑了2km到达小彬家,即点A,位置在数轴上的2处;
继续向东跑了1.5km到达小红家,即点B,位置在数轴上的$2+1.5=3.5$处;
然后又向西跑了4.5km到达学校,即点C,位置在数轴上的$3.5 - 4.5 = -1$处;
最后又向东跑回到自己家,即原点0。
在数轴上标出这些点,得到:
A点在2的位置,B点在3.5的位置,C点在-1的位置。
数轴图略。
(2)小彬家与学校之间的距离是数轴上点A与点C之间的距离,即$|2 - (-1)| = 3(km)$。
(3)小明跑步的总路程是各段路程的绝对值之和,
即$|2| + |1.5| + |-4.5| + |-1-0| = 2 + 1.5 + 4.5 + 1 = 9(km)$。
换算成米,即$9km = 9000m$。
根据速度等于路程除以时间的公式,时间$t = \frac{9000}{250} = 36(min)$。
【答案】:
(1)数轴图略;
(2)小彬家与学校之间的距离是$3km$;
(3)小明跑步一共用了$36min$。
8. 下列说法正确的是 (
A.有理数都可以用数轴上的点来表示
B.数轴上到原点的距离为 $ 2025 $ 的点有且只有 $ 1 $ 个
C.数轴上找不到既不表示正数也不表示负数的点
D.数轴上表示 $ -2 $ 的点一定在原点的右边
A
)A.有理数都可以用数轴上的点来表示
B.数轴上到原点的距离为 $ 2025 $ 的点有且只有 $ 1 $ 个
C.数轴上找不到既不表示正数也不表示负数的点
D.数轴上表示 $ -2 $ 的点一定在原点的右边
答案:【解析】:
本题主要考察数轴的基本概念和性质。
A选项:有理数都可以用数轴上的点来表示。这是数轴的基本定义,每一个有理数都对应数轴上的一个点,所以A选项是正确的。
B选项:数轴上到原点的距离为$2025$的点有且只有$1$个。实际上,数轴上到原点的距离为某个正数的点有两个,一个在正方向,一个在负方向。因此,到原点距离为$2025$的点应该是$2025$和$-2025$,所以B选项是错误的。
C选项:数轴上找不到既不表示正数也不表示负数的点。实际上,数轴上的原点($0$点)既不表示正数也不表示负数,所以C选项是错误的。
D选项:数轴上表示$-2$的点一定在原点的右边。实际上,$-2$在数轴上位于原点的左侧,所以D选项是错误的。
综上所述,只有A选项是正确的。
【答案】:
A
本题主要考察数轴的基本概念和性质。
A选项:有理数都可以用数轴上的点来表示。这是数轴的基本定义,每一个有理数都对应数轴上的一个点,所以A选项是正确的。
B选项:数轴上到原点的距离为$2025$的点有且只有$1$个。实际上,数轴上到原点的距离为某个正数的点有两个,一个在正方向,一个在负方向。因此,到原点距离为$2025$的点应该是$2025$和$-2025$,所以B选项是错误的。
C选项:数轴上找不到既不表示正数也不表示负数的点。实际上,数轴上的原点($0$点)既不表示正数也不表示负数,所以C选项是错误的。
D选项:数轴上表示$-2$的点一定在原点的右边。实际上,$-2$在数轴上位于原点的左侧,所以D选项是错误的。
综上所述,只有A选项是正确的。
【答案】:
A
9. (2025·江苏无锡期末)一只蚂蚁从数轴上点 $ A $ 处出发爬了 $ 4 $ 个单位长度到达原点,则点 $ A $ 表示的数是 (
A.$ 2 $ 或 $ -2 $
B.$ 4 $ 或 $ -4 $
C.$ 4 $
D.$ -4 $
B
)A.$ 2 $ 或 $ -2 $
B.$ 4 $ 或 $ -4 $
C.$ 4 $
D.$ -4 $
答案:【解析】:
首先,我们明确数轴上的点与原点之间的距离表示该点的数的绝对值。
设点A表示的数为$x$,根据题意,蚂蚁从点A爬了4个单位长度到达原点,即$|x| = 4$。
解这个绝对值方程,我们得到两个可能的
$x = 4$ 或 $x = -4$。
这是因为一个数到原点的距离等于4,那么这个数可以是4或者-4。
【答案】:
B. $4$ 或 $-4$。
首先,我们明确数轴上的点与原点之间的距离表示该点的数的绝对值。
设点A表示的数为$x$,根据题意,蚂蚁从点A爬了4个单位长度到达原点,即$|x| = 4$。
解这个绝对值方程,我们得到两个可能的
$x = 4$ 或 $x = -4$。
这是因为一个数到原点的距离等于4,那么这个数可以是4或者-4。
【答案】:
B. $4$ 或 $-4$。