1. 下列说法正确的是(
A.连接两点的线段叫作这两点之间的距离
B.线段的中点到线段两个端点的距离相等
C.到线段两个端点距离相等的点叫作线段的中点
D.若 $ AB = BC $,则 $ B $ 是线段 $ AC $ 的中点
B
)A.连接两点的线段叫作这两点之间的距离
B.线段的中点到线段两个端点的距离相等
C.到线段两个端点距离相等的点叫作线段的中点
D.若 $ AB = BC $,则 $ B $ 是线段 $ AC $ 的中点
答案:【解析】:
本题考察的是对线段相关概念的理解。
A选项:连接两点的线段的长度才叫作这两点之间的距离,而不是线段本身,所以A选项错误。
B选项:根据线段中点的定义,线段的中点到线段两个端点的距离是相等的,所以B选项正确。
C选项:到线段两个端点距离相等的点不一定在线段上,因此不一定是线段的中点,所以C选项错误。
D选项:若$AB = BC$,但A、B、C三点不在同一直线上,则B不是线段AC的中点,所以D选项错误。
综上所述,只有B选项是正确的。
【答案】:
B
本题考察的是对线段相关概念的理解。
A选项:连接两点的线段的长度才叫作这两点之间的距离,而不是线段本身,所以A选项错误。
B选项:根据线段中点的定义,线段的中点到线段两个端点的距离是相等的,所以B选项正确。
C选项:到线段两个端点距离相等的点不一定在线段上,因此不一定是线段的中点,所以C选项错误。
D选项:若$AB = BC$,但A、B、C三点不在同一直线上,则B不是线段AC的中点,所以D选项错误。
综上所述,只有B选项是正确的。
【答案】:
B
2. 已知点 $ C $ 在线段 $ AB $ 上,则下列条件中,不能确定 $ C $ 是线段 $ AB $ 的中点的为(
A.$ AC = BC $
B.$ AB = 2AC $
C.$ AC + BC = AB $
D.$ BC = \frac{1}{2}AB $
C
)A.$ AC = BC $
B.$ AB = 2AC $
C.$ AC + BC = AB $
D.$ BC = \frac{1}{2}AB $
答案:【解析】:
本题主要考察线段中点的定义及其性质。
线段中点的定义是:若点C在线段AB上,且$AC = BC$,则点C是线段AB的中点。
或者,若点C在线段AB上,且$AB = 2AC$(或$AB = 2BC$),则点C也是线段AB的中点。
或者,若点C在线段AB上,且$BC = \frac{1}{2}AB$(或$AC = \frac{1}{2}AB$),则点C还是线段AB的中点。
对于选项A:$AC = BC$,直接符合线段中点的定义,所以能确定C是线段AB的中点。
对于选项B:$AB = 2AC$,根据线段中点的性质,这也能确定C是线段AB的中点。
对于选项C:$AC + BC = AB$,这个条件只能说明点C在线段AB上,但不能确定C是AB的中点,因为对于线段AB上的任意点C(除了A和B),这个等式都成立。
对于选项D:$BC = \frac{1}{2}AB$,根据线段中点的性质,这同样能确定C是线段AB的中点。
综上所述,只有选项C不能确定C是线段AB的中点。
【答案】:
C
本题主要考察线段中点的定义及其性质。
线段中点的定义是:若点C在线段AB上,且$AC = BC$,则点C是线段AB的中点。
或者,若点C在线段AB上,且$AB = 2AC$(或$AB = 2BC$),则点C也是线段AB的中点。
或者,若点C在线段AB上,且$BC = \frac{1}{2}AB$(或$AC = \frac{1}{2}AB$),则点C还是线段AB的中点。
对于选项A:$AC = BC$,直接符合线段中点的定义,所以能确定C是线段AB的中点。
对于选项B:$AB = 2AC$,根据线段中点的性质,这也能确定C是线段AB的中点。
对于选项C:$AC + BC = AB$,这个条件只能说明点C在线段AB上,但不能确定C是AB的中点,因为对于线段AB上的任意点C(除了A和B),这个等式都成立。
对于选项D:$BC = \frac{1}{2}AB$,根据线段中点的性质,这同样能确定C是线段AB的中点。
综上所述,只有选项C不能确定C是线段AB的中点。
【答案】:
C
3. (2025·江苏无锡期末)如图,点 $ C $ 在线段 $ AB $ 的延长线上,且 $ BC = \frac{1}{2}AB $,$ D $ 是 $ AC $ 的中点. 若 $ DC = 3 $,则 $ AB $ 的长是(
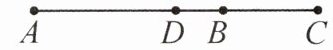
A.3
B.4
C.5
D.6
B
)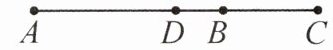
A.3
B.4
C.5
D.6
答案:【解析】:本题主要考查线段的长短关系以及中点的性质。
已知$D$是$AC$的中点,且$DC = 3$,根据中点的定义,可知$AC = 2DC$,所以$AC = 2×3 = 6$。
设$AB = x$,因为$BC=\frac{1}{2}AB$,所以$BC=\frac{1}{2}x$。
又因为$AC = AB + BC$,即$x+\frac{1}{2}x = 6$。
合并同类项可得$\frac{3}{2}x = 6$,两边同时除以$\frac{3}{2}$,解得$x = 4$,即$AB = 4$。
【答案】:B
已知$D$是$AC$的中点,且$DC = 3$,根据中点的定义,可知$AC = 2DC$,所以$AC = 2×3 = 6$。
设$AB = x$,因为$BC=\frac{1}{2}AB$,所以$BC=\frac{1}{2}x$。
又因为$AC = AB + BC$,即$x+\frac{1}{2}x = 6$。
合并同类项可得$\frac{3}{2}x = 6$,两边同时除以$\frac{3}{2}$,解得$x = 4$,即$AB = 4$。
【答案】:B
4. 如图,$ C $ 是线段 $ AB $ 的中点. 若 $ AC = 2\mathrm{cm} $,则 $ AB = $
4
$\mathrm{cm}$.答案:【解析】:本题主要考查了线段中点的性质。
根据线段中点的定义,若C是线段AB的中点,则$AC = BC=\frac{1}{2}AB$。
已知$AC = 2cm$,因为C是AB中点,所以$AB = 2AC$。
将$AC = 2cm$代入$AB = 2AC$,可得$AB=2×2 = 4cm$。
【答案】:$4$
根据线段中点的定义,若C是线段AB的中点,则$AC = BC=\frac{1}{2}AB$。
已知$AC = 2cm$,因为C是AB中点,所以$AB = 2AC$。
将$AC = 2cm$代入$AB = 2AC$,可得$AB=2×2 = 4cm$。
【答案】:$4$
5. 已知线段 $ AB = 2\mathrm{cm} $,延长 $ AB $ 到点 $ C $,使 $ BC = AB $,再延长 $ BA $ 到点 $ D $,使 $ BD = 2AB $,则线段 $ CD $ 的长为
6
$\mathrm{cm}$.答案:解:
∵ $ AB = 2\mathrm{cm} $,延长 $ AB $ 到点 $ C $,使 $ BC = AB $,
∴ $ BC = AB = 2\mathrm{cm} $,$ AC = AB + BC = 2 + 2 = 4\mathrm{cm} $。
∵ 延长 $ BA $ 到点 $ D $,使 $ BD = 2AB $,
∴ $ BD = 2 × 2 = 4\mathrm{cm} $。
又∵ $ AD = BD - AB = 4 - 2 = 2\mathrm{cm} $,
∴ $ CD = AD + AC = 2 + 4 = 6\mathrm{cm} $。
答案:$ 6 $
∵ $ AB = 2\mathrm{cm} $,延长 $ AB $ 到点 $ C $,使 $ BC = AB $,
∴ $ BC = AB = 2\mathrm{cm} $,$ AC = AB + BC = 2 + 2 = 4\mathrm{cm} $。
∵ 延长 $ BA $ 到点 $ D $,使 $ BD = 2AB $,
∴ $ BD = 2 × 2 = 4\mathrm{cm} $。
又∵ $ AD = BD - AB = 4 - 2 = 2\mathrm{cm} $,
∴ $ CD = AD + AC = 2 + 4 = 6\mathrm{cm} $。
答案:$ 6 $
6. (教材 P161 习题 6 变式)如图,$ AB = 8\mathrm{cm} $,延长 $ AB $ 到点 $ C $,使 $ BC = 2AB $. 若 $ D $ 是 $ AC $ 的中点,则 $ BD = $
4
$\mathrm{cm}$.答案:【解析】:本题主要考查了线段长短的比较与计算,解题的关键是利用中点的性质以及线段之间的长度关系进行求解。
已知$AB = 8cm$,$BC = 2AB$,所以$BC = 2×8 = 16cm$。
因为$AC = AB + BC$,所以$AC = 8 + 16 = 24cm$。
又因为$D$是$AC$的中点,根据中点的性质,中点将线段分为相等的两部分,所以$AD=\frac{1}{2}AC=\frac{1}{2}×24 = 12cm$。
而$BD = AD - AB$,所以$BD = 12 - 8 = 4cm$。
【答案】:$4$
已知$AB = 8cm$,$BC = 2AB$,所以$BC = 2×8 = 16cm$。
因为$AC = AB + BC$,所以$AC = 8 + 16 = 24cm$。
又因为$D$是$AC$的中点,根据中点的性质,中点将线段分为相等的两部分,所以$AD=\frac{1}{2}AC=\frac{1}{2}×24 = 12cm$。
而$BD = AD - AB$,所以$BD = 12 - 8 = 4cm$。
【答案】:$4$
7. 如图,平面上有射线 $ AP $ 和点 $ B $,$ C $,请用无刻度的直尺和圆规按下列要求作图:
(1) 连接 $ AB $,并在射线 $ AP $ 上截取 $ AD = AB $;
(2) 连接 $ BC $,并延长 $ BC $ 到点 $ E $,使 $ CE = 2BC $.

(1) 连接 $ AB $,并在射线 $ AP $ 上截取 $ AD = AB $;
(2) 连接 $ BC $,并延长 $ BC $ 到点 $ E $,使 $ CE = 2BC $.

答案:答案略
解析:
(1)①用直尺连接点A和点B,得到线段AB;②以点A为圆心,AB长为半径画弧,交射线AP于点D,AD即为所求。
(2)①用直尺连接点B和点C,得到线段BC;②以点C为圆心,BC长为半径画弧,交BC延长线于点F;③以点F为圆心,BC长为半径画弧,交BC延长线于点E,点E即为所求。
(2)①用直尺连接点B和点C,得到线段BC;②以点C为圆心,BC长为半径画弧,交BC延长线于点F;③以点F为圆心,BC长为半径画弧,交BC延长线于点E,点E即为所求。
8. 如图,$ C $ 是线段 $ AB $ 的中点,$ D $ 是线段 $ BC $ 的中点,给出下列等式:① $ CD = AC - BD $;② $ CD = AD - BC $;③ $ BD = 2AD - AB $;④ $ CD = \frac{1}{3}AB $. 其中正确的有(

A.4 个
B.3 个
C.2 个
D.1 个
C
)
A.4 个
B.3 个
C.2 个
D.1 个
答案:【解析】:本题主要考查了线段的中点性质以及线段之间的数量关系。
① $CD = AC - BD$
由于$C$是$AB$的中点,$D$是$BC$的中点,
所以,$AC = CB$,$CD = DB$,
那么,$CD = CB - BD = AC - BD$,
故①正确。
② $CD = AD - BC$
由于$C$是$AB$的中点,$D$是$BC$的中点,
所以,$BC=AC$,$CD=BD=\frac{1}{2}BC$,
那么,$AD=AC+CD=AC+\frac{1}{2}BC=\frac{3}{2}BC$,
所以,$AD-BC=\frac{3}{2}BC-BC=\frac{1}{2}BC=CD$,
故②正确。
③ $BD = 2AD - AB$
由于$C$是$AB$的中点,$D$是$BC$的中点,
所以,$AD = AC + CD = \frac{1}{2}AB+ \frac{1}{4}AB = \frac{3}{4}AB$,
那么,$2AD = \frac{3}{2}AB$,
所以,$2AD - AB = \frac{3}{2}AB - AB = \frac{1}{2}AB$,
又因为$BD = \frac{1}{2}BC=\frac{1}{4}AB$,
所以,$BD\neq 2AD - AB$,
故③错误。
④ $CD = \frac{1}{3}AB$
由于$D$是$BC$的中点,
所以,$CD = \frac{1}{2}BC$,
又因为$C$是$AB$的中点,
所以,$BC = \frac{1}{2}AB$,
那么,$CD = \frac{1}{2} × \frac{1}{2}AB = \frac{1}{4}AB$,
所以,$CD \neq \frac{1}{3}AB$,
故④错误。
正确的等式有2个,
故选C。
【答案】:C。
① $CD = AC - BD$
由于$C$是$AB$的中点,$D$是$BC$的中点,
所以,$AC = CB$,$CD = DB$,
那么,$CD = CB - BD = AC - BD$,
故①正确。
② $CD = AD - BC$
由于$C$是$AB$的中点,$D$是$BC$的中点,
所以,$BC=AC$,$CD=BD=\frac{1}{2}BC$,
那么,$AD=AC+CD=AC+\frac{1}{2}BC=\frac{3}{2}BC$,
所以,$AD-BC=\frac{3}{2}BC-BC=\frac{1}{2}BC=CD$,
故②正确。
③ $BD = 2AD - AB$
由于$C$是$AB$的中点,$D$是$BC$的中点,
所以,$AD = AC + CD = \frac{1}{2}AB+ \frac{1}{4}AB = \frac{3}{4}AB$,
那么,$2AD = \frac{3}{2}AB$,
所以,$2AD - AB = \frac{3}{2}AB - AB = \frac{1}{2}AB$,
又因为$BD = \frac{1}{2}BC=\frac{1}{4}AB$,
所以,$BD\neq 2AD - AB$,
故③错误。
④ $CD = \frac{1}{3}AB$
由于$D$是$BC$的中点,
所以,$CD = \frac{1}{2}BC$,
又因为$C$是$AB$的中点,
所以,$BC = \frac{1}{2}AB$,
那么,$CD = \frac{1}{2} × \frac{1}{2}AB = \frac{1}{4}AB$,
所以,$CD \neq \frac{1}{3}AB$,
故④错误。
正确的等式有2个,
故选C。
【答案】:C。
9. 已知线段 $ AB = 4 $,在直线 $ AB $ 上作线段 $ BC $,使得 $ BC = 2 $. 若 $ D $ 是线段 $ AC $ 的中点,则线段 $ AD $ 的长为(
A.1
B.3
C.1 或 3
D.2 或 3
C
)A.1
B.3
C.1 或 3
D.2 或 3
答案:【解析】:
本题主要考查了线段的长短计算以及中点的性质。
首先,需要考虑线段$BC$相对于线段$AB$的两种可能位置:
当点$C$位于线段$AB$上时,
可以通过线段的长度加减来计算$AC$的长度,
即:$AC = AB - BC = 4 - 2 = 2$,
由于$D$是线段$AC$的中点,
根据中点的性质,有$AD = \frac{1}{2}AC = \frac{1}{2} × 2 = 1$,
当点$C$位于线段$AB$的延长线上时,
同样可以通过线段的长度加减来计算$AC$的长度,
即:$AC = AB + BC = 4 + 2 = 6$,
由于$D$是线段$AC$的中点,
根据中点的性质,有:
$AD = \frac{1}{2}AC = \frac{1}{2} × 6 = 3$,
综合以上两种情况,得出线段$AD$的长为$1$或$3$。
【答案】:
C. $1$或$3$。
本题主要考查了线段的长短计算以及中点的性质。
首先,需要考虑线段$BC$相对于线段$AB$的两种可能位置:
当点$C$位于线段$AB$上时,
可以通过线段的长度加减来计算$AC$的长度,
即:$AC = AB - BC = 4 - 2 = 2$,
由于$D$是线段$AC$的中点,
根据中点的性质,有$AD = \frac{1}{2}AC = \frac{1}{2} × 2 = 1$,
当点$C$位于线段$AB$的延长线上时,
同样可以通过线段的长度加减来计算$AC$的长度,
即:$AC = AB + BC = 4 + 2 = 6$,
由于$D$是线段$AC$的中点,
根据中点的性质,有:
$AD = \frac{1}{2}AC = \frac{1}{2} × 6 = 3$,
综合以上两种情况,得出线段$AD$的长为$1$或$3$。
【答案】:
C. $1$或$3$。
10. 新素养 推理能力 (2025·江苏苏州期末)互不重合的 $ A $,$ B $,$ C $ 三点在同一条直线上. 若 $ AC = 2a + 1 $,$ BC = a + 4 $,$ AB = 3a $,则这三点之间的位置关系是(
A.点 $ A $ 在 $ B $,$ C $ 两点之间
B.点 $ B $ 在 $ A $,$ C $ 两点之间
C.点 $ C $ 在 $ A $,$ B $ 两点之间
D.无法确定
A
)A.点 $ A $ 在 $ B $,$ C $ 两点之间
B.点 $ B $ 在 $ A $,$ C $ 两点之间
C.点 $ C $ 在 $ A $,$ B $ 两点之间
D.无法确定
答案:解:分三种情况讨论:
情况1:若点A在B,C两点之间,则AB + AC = BC。
即3a + (2a + 1) = a + 4
5a + 1 = a + 4
4a = 3
a = 3/4
此时AC = 2*(3/4) + 1 = 5/2,BC = 3/4 + 4 = 19/4,AB = 3*(3/4) = 9/4
因为AB + AC = 9/4 + 5/2 = 19/4 = BC,所以此情况成立。
情况2:若点B在A,C两点之间,则AB + BC = AC。
即3a + (a + 4) = 2a + 1
4a + 4 = 2a + 1
2a = -3
a = -3/2
此时AB = 3*(-3/2) = -9/2,线段长度不能为负,此情况不成立。
情况3:若点C在A,B两点之间,则AC + BC = AB。
即(2a + 1) + (a + 4) = 3a
3a + 5 = 3a
5 = 0,等式不成立,此情况不成立。
综上,三点位置关系为点A在B,C两点之间。
答案:A
情况1:若点A在B,C两点之间,则AB + AC = BC。
即3a + (2a + 1) = a + 4
5a + 1 = a + 4
4a = 3
a = 3/4
此时AC = 2*(3/4) + 1 = 5/2,BC = 3/4 + 4 = 19/4,AB = 3*(3/4) = 9/4
因为AB + AC = 9/4 + 5/2 = 19/4 = BC,所以此情况成立。
情况2:若点B在A,C两点之间,则AB + BC = AC。
即3a + (a + 4) = 2a + 1
4a + 4 = 2a + 1
2a = -3
a = -3/2
此时AB = 3*(-3/2) = -9/2,线段长度不能为负,此情况不成立。
情况3:若点C在A,B两点之间,则AC + BC = AB。
即(2a + 1) + (a + 4) = 3a
3a + 5 = 3a
5 = 0,等式不成立,此情况不成立。
综上,三点位置关系为点A在B,C两点之间。
答案:A