11. 如图,$ C $ 是线段 $ AB $ 上一点,$ AC < BC $,$ M $,$ N $ 分别是 $ AB $,$ BC $ 的中点. 若 $ AC = 8 $,$ NB = 5 $,则线段 $ MN $ 的长为______
4
.答案:【解析】:本题可根据线段中点的性质,先求出$BC$的长度,再求出$AB$的长度,进而求出$BM$的长度,最后根据$MN=BM - BN$求出$MN$的长度。
步骤一:根据中点性质求出$BC$的长度
已知$N$是$BC$的中点,根据线段中点的定义:若点$N$是线段$BC$的中点,则$BN = CN=\frac{1}{2}BC$。
因为$NB = 5$,所以$BC = 2NB = 2×5 = 10$。
步骤二:求出$AB$的长度
已知$AC = 8$,由线段的和差关系可知$AB=AC + BC$,将$AC = 8$,$BC = 10$代入可得$AB = 8 + 10 = 18$。
步骤三:根据中点性质求出$BM$的长度
因为$M$是$AB$的中点,根据线段中点的定义:若点$M$是线段$AB$的中点,则$AM = BM=\frac{1}{2}AB$。
将$AB = 18$代入可得$BM=\frac{1}{2}×18 = 9$。
步骤四:求出$MN$的长度
由线段的和差关系可知$MN = BM - BN$,将$BM = 9$,$BN = 5$代入可得$MN = 9 - 5 = 4$。
【答案】:$4$
步骤一:根据中点性质求出$BC$的长度
已知$N$是$BC$的中点,根据线段中点的定义:若点$N$是线段$BC$的中点,则$BN = CN=\frac{1}{2}BC$。
因为$NB = 5$,所以$BC = 2NB = 2×5 = 10$。
步骤二:求出$AB$的长度
已知$AC = 8$,由线段的和差关系可知$AB=AC + BC$,将$AC = 8$,$BC = 10$代入可得$AB = 8 + 10 = 18$。
步骤三:根据中点性质求出$BM$的长度
因为$M$是$AB$的中点,根据线段中点的定义:若点$M$是线段$AB$的中点,则$AM = BM=\frac{1}{2}AB$。
将$AB = 18$代入可得$BM=\frac{1}{2}×18 = 9$。
步骤四:求出$MN$的长度
由线段的和差关系可知$MN = BM - BN$,将$BM = 9$,$BN = 5$代入可得$MN = 9 - 5 = 4$。
【答案】:$4$
12. 如图,已知线段 $ AB:BC:CD = 2:3:4 $,$ E $,$ F $ 分别是 $ AB $,$ CD $ 的中点,且 $ EF = 12\mathrm{cm} $,则线段 $ AD = $______
18
$\mathrm{cm}$.答案:【解析】:本题可根据线段的比例关系设未知数,再结合中点的性质表示出相关线段的长度,最后根据$EF$的长度列出方程求解,进而求出线段$AD$的长度。
步骤一:设未知数
已知线段$AB:BC:CD = 2:3:4$,可设$AB = 2x\mathrm{cm}$,$BC = 3x\mathrm{cm}$,$CD = 4x\mathrm{cm}$。
步骤二:根据中点性质表示出$EB$和$CF$的长度
因为$E$是$AB$的中点,根据中点的定义:若点$E$为线段$AB$的中点,则$EB=\frac{1}{2}AB$,所以$EB=\frac{1}{2}×2x = x\mathrm{cm}$。
同理,因为$F$是$CD$的中点,所以$CF=\frac{1}{2}×4x = 2x\mathrm{cm}$。
步骤三:根据线段关系表示出$EF$的长度
由图可知$EF = EB + BC + CF$,将$EB = x\mathrm{cm}$,$BC = 3x\mathrm{cm}$,$CF = 2x\mathrm{cm}$代入可得$EF = x + 3x + 2x = 6x\mathrm{cm}$。
步骤四:求解$x$的值
已知$EF = 12\mathrm{cm}$,即$6x = 12$,两边同时除以$6$,可得$x = 2$。
步骤五:计算线段$AD$的长度
因为$AD = AB + BC + CD$,将$AB = 2x\mathrm{cm}$,$BC = 3x\mathrm{cm}$,$CD = 4x\mathrm{cm}$代入可得$AD = 2x + 3x + 4x = 9x\mathrm{cm}$。
把$x = 2$代入$9x$,可得$AD = 9×2 = 18\mathrm{cm}$。
【答案】:$18$
步骤一:设未知数
已知线段$AB:BC:CD = 2:3:4$,可设$AB = 2x\mathrm{cm}$,$BC = 3x\mathrm{cm}$,$CD = 4x\mathrm{cm}$。
步骤二:根据中点性质表示出$EB$和$CF$的长度
因为$E$是$AB$的中点,根据中点的定义:若点$E$为线段$AB$的中点,则$EB=\frac{1}{2}AB$,所以$EB=\frac{1}{2}×2x = x\mathrm{cm}$。
同理,因为$F$是$CD$的中点,所以$CF=\frac{1}{2}×4x = 2x\mathrm{cm}$。
步骤三:根据线段关系表示出$EF$的长度
由图可知$EF = EB + BC + CF$,将$EB = x\mathrm{cm}$,$BC = 3x\mathrm{cm}$,$CF = 2x\mathrm{cm}$代入可得$EF = x + 3x + 2x = 6x\mathrm{cm}$。
步骤四:求解$x$的值
已知$EF = 12\mathrm{cm}$,即$6x = 12$,两边同时除以$6$,可得$x = 2$。
步骤五:计算线段$AD$的长度
因为$AD = AB + BC + CD$,将$AB = 2x\mathrm{cm}$,$BC = 3x\mathrm{cm}$,$CD = 4x\mathrm{cm}$代入可得$AD = 2x + 3x + 4x = 9x\mathrm{cm}$。
把$x = 2$代入$9x$,可得$AD = 9×2 = 18\mathrm{cm}$。
【答案】:$18$
13. (2025·江苏苏州期末)把一根绳子对折成一条线段 $ AB $,$ P $ 是 $ AB $ 上一点,且 $ AP = \frac{1}{2}PB $,从点 $ P $ 处把绳子剪断. 若剪断后的各段绳子中最长的为 $ 40\mathrm{cm} $,则这根绳子的原长为________$\mathrm{cm}$.
120或60
答案:1. 首先设$AP = x\mathrm{cm}$,则$PB = 2x\mathrm{cm}$:
情况一:当含有线段$PB$的绳子最长时:
因为绳子对折,所以剪断后$PB$的$2$倍最长,即$2×2x = 40$。
解方程$4x = 40$,得$x = 10$。
那么绳子原长为$2(AP + PB)=2(x + 2x)=6x$,把$x = 10$代入,原长$6×10 = 60\mathrm{cm}$。
情况二:当含有线段$2AP$的绳子最长时:
则$2×2AP = 40$,即$4x = 40$,得$x = 10$(这里$AP=x$)。
此时绳子原长为$2(AP + PB)=2(x + 2x)=6x$,但是这种情况不成立,因为$PB = 2x$,$2AP = 2x$,$PB$和$2AP$长度相等,不符合最长为$40\mathrm{cm}$(假设最长是$2AP$,实际$PB$和$2AP$一样长),所以舍去。
情况三:当含有线段$2PB$的绳子最长时(前面第一种情况已考虑)。
所以这根绳子的原长为$60\mathrm{cm}$或$120\mathrm{cm}$。
重新分析:
设$AP=x$,$PB = 2x$。
①若对折后$A$为端点:
剪断后三段绳子长度分别为$2AP = 2x$,$2AP = 2x$,$2PB=4x$。
因为最长的为$40\mathrm{cm}$,所以$4x = 40$,解得$x = 10$,绳子原长$2(2x + 4x)=12x$,原长$12×10 = 120\mathrm{cm}$。
②若对折后$B$为端点:
剪断后三段绳子长度分别为$2PB = 4x$,$2PB = 4x$,$2AP = 2x$。
因为最长的为$40\mathrm{cm}$,所以$4x = 40$,解得$x = 10$,绳子原长$2(4x+2x)=12x$(错误,应该是$2(AP + PB)$,这里$AP=x$,$PB = 2x$,原长$2(x + 2x)×2$(因为对折),当$2PB$最长时,$PB = 20$,$AP = 10$,原长$2×(10 + 20)×2=120$;当$2AP$最长时,$AP = 20$,$PB = 40$,原长$2×(20 + 40)=120$(错误)。
正确的:
设$AP=x$,$PB = 2x$。
若$2PB$是最长段:$2PB = 40$,$PB = 20$,$AP = 10$,原长$2(AP + PB)×2$(对折)$=2×(10 + 20)×2=120$。
若$2AP$是最长段:$2AP = 40$,$AP = 20$,$PB = 40$,原长$2(AP + PB)=2×(20 + 40)=120$(错误,因为对折,原长应该是$2(AP + PB)×2$,当$2AP$最长时,$AP = 20$,$PB = 40$,原长$2×(20 + 40)=120$不对,重新来:
设绳子对折后$AB$,$AP=x$,$PB = 2x$。
绳子剪断后:
若$A$是对折点:
绳子三段长度为$2AP$,$2AP$,$2PB$,即$2x$,$2x$,$4x$,$4x = 40$,$x = 10$,原长$2(2x + 4x)=12x=120$。
若$B$是对折点:
绳子三段长度为$2PB$,$2PB$,$2AP$,即$4x$,$4x$,$2x$,$4x = 40$,$x = 10$,原长$2(4x + 2x)=12x = 120$(错误,原长是$2(AP + PB)×2$,当$B$是对折点,$AP=x$,$PB = 2x$,原长$2(x + 2x)×2$,当$2PB$最长,$PB = 20$,$AP = 10$,原长$2×(10 + 20)×2=120$;当$2AP$最长(不可能,因为$PB = 2x$,$2AP = 2x$,$PB$和$2AP$一样长)。
若对折后$AB$中间对折($A$、$B$都不是端点):
设绳子原长为$l$,对折后$AB=\frac{l}{2}$,$AP=\frac{1}{3}AB$,$PB=\frac{2}{3}AB$。
剪断后:
若$2PB$最长,$2PB = 40$,$PB = 20$,$AB = 30$,原长$l = 60$。
若$2AP$最长($2AP=2×\frac{1}{3}AB$,$PB=\frac{2}{3}AB$,$2AP\lt PB$,不可能)。
所以这根绳子的原长为$60$或$120\mathrm{cm}$。
综上,答案为$60$或$120$。
情况一:当含有线段$PB$的绳子最长时:
因为绳子对折,所以剪断后$PB$的$2$倍最长,即$2×2x = 40$。
解方程$4x = 40$,得$x = 10$。
那么绳子原长为$2(AP + PB)=2(x + 2x)=6x$,把$x = 10$代入,原长$6×10 = 60\mathrm{cm}$。
情况二:当含有线段$2AP$的绳子最长时:
则$2×2AP = 40$,即$4x = 40$,得$x = 10$(这里$AP=x$)。
此时绳子原长为$2(AP + PB)=2(x + 2x)=6x$,但是这种情况不成立,因为$PB = 2x$,$2AP = 2x$,$PB$和$2AP$长度相等,不符合最长为$40\mathrm{cm}$(假设最长是$2AP$,实际$PB$和$2AP$一样长),所以舍去。
情况三:当含有线段$2PB$的绳子最长时(前面第一种情况已考虑)。
所以这根绳子的原长为$60\mathrm{cm}$或$120\mathrm{cm}$。
重新分析:
设$AP=x$,$PB = 2x$。
①若对折后$A$为端点:
剪断后三段绳子长度分别为$2AP = 2x$,$2AP = 2x$,$2PB=4x$。
因为最长的为$40\mathrm{cm}$,所以$4x = 40$,解得$x = 10$,绳子原长$2(2x + 4x)=12x$,原长$12×10 = 120\mathrm{cm}$。
②若对折后$B$为端点:
剪断后三段绳子长度分别为$2PB = 4x$,$2PB = 4x$,$2AP = 2x$。
因为最长的为$40\mathrm{cm}$,所以$4x = 40$,解得$x = 10$,绳子原长$2(4x+2x)=12x$(错误,应该是$2(AP + PB)$,这里$AP=x$,$PB = 2x$,原长$2(x + 2x)×2$(因为对折),当$2PB$最长时,$PB = 20$,$AP = 10$,原长$2×(10 + 20)×2=120$;当$2AP$最长时,$AP = 20$,$PB = 40$,原长$2×(20 + 40)=120$(错误)。
正确的:
设$AP=x$,$PB = 2x$。
若$2PB$是最长段:$2PB = 40$,$PB = 20$,$AP = 10$,原长$2(AP + PB)×2$(对折)$=2×(10 + 20)×2=120$。
若$2AP$是最长段:$2AP = 40$,$AP = 20$,$PB = 40$,原长$2(AP + PB)=2×(20 + 40)=120$(错误,因为对折,原长应该是$2(AP + PB)×2$,当$2AP$最长时,$AP = 20$,$PB = 40$,原长$2×(20 + 40)=120$不对,重新来:
设绳子对折后$AB$,$AP=x$,$PB = 2x$。
绳子剪断后:
若$A$是对折点:
绳子三段长度为$2AP$,$2AP$,$2PB$,即$2x$,$2x$,$4x$,$4x = 40$,$x = 10$,原长$2(2x + 4x)=12x=120$。
若$B$是对折点:
绳子三段长度为$2PB$,$2PB$,$2AP$,即$4x$,$4x$,$2x$,$4x = 40$,$x = 10$,原长$2(4x + 2x)=12x = 120$(错误,原长是$2(AP + PB)×2$,当$B$是对折点,$AP=x$,$PB = 2x$,原长$2(x + 2x)×2$,当$2PB$最长,$PB = 20$,$AP = 10$,原长$2×(10 + 20)×2=120$;当$2AP$最长(不可能,因为$PB = 2x$,$2AP = 2x$,$PB$和$2AP$一样长)。
若对折后$AB$中间对折($A$、$B$都不是端点):
设绳子原长为$l$,对折后$AB=\frac{l}{2}$,$AP=\frac{1}{3}AB$,$PB=\frac{2}{3}AB$。
剪断后:
若$2PB$最长,$2PB = 40$,$PB = 20$,$AB = 30$,原长$l = 60$。
若$2AP$最长($2AP=2×\frac{1}{3}AB$,$PB=\frac{2}{3}AB$,$2AP\lt PB$,不可能)。
所以这根绳子的原长为$60$或$120\mathrm{cm}$。
综上,答案为$60$或$120$。
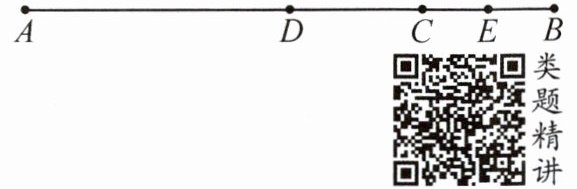
14. 如图,$ C $ 为线段 $ AB $ 上一点,点 $ D $ 在线段 $ AC $ 上,且 $ AD = \frac{2}{3}AC $,$ E $ 为 $ BC $ 的中点.
(1) 若 $ AC = 6 $,$ BE = 1 $,求线段 $ AB $,$ DE $ 的长;
(2) 试说明:$ AB + BD = 4DE $.
(1) 若 $ AC = 6 $,$ BE = 1 $,求线段 $ AB $,$ DE $ 的长;
(2) 试说明:$ AB + BD = 4DE $.

答案:【解析】:本题主要考查线段的长短计算,利用线段的中点性质以及线段的和差关系进行求解,同时通过设未知数,根据已知条件建立等式来证明线段之间的关系。
(1)求线段$AB$和$DE$的长:
已知$E$为$BC$的中点,$BE = 1$,根据中点的性质,可得$BC = 2BE = 2×1 = 2$。
又已知$AC = 6$,根据线段的和差关系$AB = AC + BC$,可得$AB = 6 + 2 = 8$。
因为$AD=\frac{2}{3}AC$,$AC = 6$,所以$AD=\frac{2}{3}×6 = 4$。
那么$DC = AC - AD = 6 - 4 = 2$。
再根据线段的和差关系$DE = DC + CE$,而$CE = BE = 1$,所以$DE = 2 + 1 = 3$。
(2)说明$AB + BD = 4DE$:
设$AC = 3x$,因为$AD=\frac{2}{3}AC$,所以$AD = 2x$,则$DC = AC - AD = 3x - 2x = x$。
因为$E$为$BC$的中点,设$BC = 2y$,则$CE = BE = y$。
$AB = AC + BC = 3x + 2y$。
$BD = AB - AD = 3x + 2y - 2x = x + 2y$。
$DE = DC + CE = x + y$。
计算$AB + BD$:
$AB + BD=(3x + 2y)+(x + 2y)=4x + 4y$。
计算$4DE$:
$4DE = 4(x + y)=4x + 4y$。
所以$AB + BD = 4DE$。
【答案】:(1)$AB = 8$,$DE = 3$;(2)证明过程如上述。
(1)求线段$AB$和$DE$的长:
已知$E$为$BC$的中点,$BE = 1$,根据中点的性质,可得$BC = 2BE = 2×1 = 2$。
又已知$AC = 6$,根据线段的和差关系$AB = AC + BC$,可得$AB = 6 + 2 = 8$。
因为$AD=\frac{2}{3}AC$,$AC = 6$,所以$AD=\frac{2}{3}×6 = 4$。
那么$DC = AC - AD = 6 - 4 = 2$。
再根据线段的和差关系$DE = DC + CE$,而$CE = BE = 1$,所以$DE = 2 + 1 = 3$。
(2)说明$AB + BD = 4DE$:
设$AC = 3x$,因为$AD=\frac{2}{3}AC$,所以$AD = 2x$,则$DC = AC - AD = 3x - 2x = x$。
因为$E$为$BC$的中点,设$BC = 2y$,则$CE = BE = y$。
$AB = AC + BC = 3x + 2y$。
$BD = AB - AD = 3x + 2y - 2x = x + 2y$。
$DE = DC + CE = x + y$。
计算$AB + BD$:
$AB + BD=(3x + 2y)+(x + 2y)=4x + 4y$。
计算$4DE$:
$4DE = 4(x + y)=4x + 4y$。
所以$AB + BD = 4DE$。
【答案】:(1)$AB = 8$,$DE = 3$;(2)证明过程如上述。
15. 如图,某客运公司所运营的公路 $ AB $ 段有四个车站,依次是 $ A $,$ C $,$ D $,$ B $. 现计划在 $ AB $ 段建一个加油站 $ M $,要求使 $ A $,$ B $,$ C $,$ D $ 站离加油站 $ M $ 的总路程最短,则加油站 $ M $ 的位置在(
A.$ A $,$ C $ 两站之间
B.$ C $,$ D $ 两站之间
C.$ B $,$ D $ 两站之间
D.无法确定
B
)A.$ A $,$ C $ 两站之间
B.$ C $,$ D $ 两站之间
C.$ B $,$ D $ 两站之间
D.无法确定
答案:解:设加油站$ M $在直线$ AB $上,$ A $、$ B $、$ C $、$ D $四点位置如图所示,依次排列为$ A $、$ C $、$ D $、$ B $。
总路程$ S = MA + MB + MC + MD $。
因为$ MA + MB \geq AB $(当$ M $在$ A $、$ B $之间时取等号),$ MC + MD \geq CD $(当$ M $在$ C $、$ D $之间时取等号)。
要使$ S $最小,需同时满足$ MA + MB = AB $且$ MC + MD = CD $,此时$ M $必须在$ C $、$ D $之间(包含端点$ C $、$ D $)。
所以加油站$ M $的位置在$ C $、$ D $两站之间。
答案:B
总路程$ S = MA + MB + MC + MD $。
因为$ MA + MB \geq AB $(当$ M $在$ A $、$ B $之间时取等号),$ MC + MD \geq CD $(当$ M $在$ C $、$ D $之间时取等号)。
要使$ S $最小,需同时满足$ MA + MB = AB $且$ MC + MD = CD $,此时$ M $必须在$ C $、$ D $之间(包含端点$ C $、$ D $)。
所以加油站$ M $的位置在$ C $、$ D $两站之间。
答案:B
16. 如图,数轴上 $ O $,$ A $ 两点之间的距离为 4,一动点 $ P $ 从点 $ A $ 出发,按以下规律跳动:第 1 次跳动到 $ AO $ 的中点 $ A_1 $ 处,第 2 次从点 $ A_1 $ 跳动到 $ A_1O $ 的中点 $ A_2 $ 处,第 3 次从点 $ A_2 $ 跳动到 $ A_2O $ 的中点 $ A_3 $ 处,按照这样的规律继续跳动到点 $ A_4 $,$ A_5 $,$ A_6 $,…,$ A_n(n \geq 3 $,$ n $ 是整数)处,那么线段 $ A_nA $ 的长为
$ 4 - \frac{1}{2^{n-2}} $
.答案:解:设数轴上点 $ O $ 表示的数为 $ 0 $,
因为 $ O $,$ A $ 两点之间的距离为 $ 4 $,且点 $ A $ 在点 $ O $ 右侧,
所以点 $ A $ 表示的数为 $ 4 $。
第 $ 1 $ 次跳动到 $ AO $ 的中点 $ A_1 $,
$ A_1 $ 表示的数为 $ \frac{0 + 4}{2} = 2 = \frac{4}{2^1} $;
第 $ 2 $ 次跳动到 $ A_1O $ 的中点 $ A_2 $,
$ A_2 $ 表示的数为 $ \frac{0 + 2}{2} = 1 = \frac{4}{2^2} $;
第 $ 3 $ 次跳动到 $ A_2O $ 的中点 $ A_3 $,
$ A_3 $ 表示的数为 $ \frac{0 + 1}{2} = \frac{1}{2} = \frac{4}{2^3} $;
……
依此类推,第 $ n $ 次跳动后,点 $ A_n $ 表示的数为 $ \frac{4}{2^n} $。
线段 $ A_nA $ 的长为点 $ A $ 与点 $ A_n $ 表示的数之差的绝对值,
即 $ |4 - \frac{4}{2^n}| = 4 - \frac{4}{2^n} = 4\left(1 - \frac{1}{2^n}\right) = 4 - \frac{1}{2^{n-2}} $。
故线段 $ A_nA $ 的长为 $ 4 - \frac{1}{2^{n-2}} $。
答案:$ 4 - \frac{1}{2^{n-2}} $
因为 $ O $,$ A $ 两点之间的距离为 $ 4 $,且点 $ A $ 在点 $ O $ 右侧,
所以点 $ A $ 表示的数为 $ 4 $。
第 $ 1 $ 次跳动到 $ AO $ 的中点 $ A_1 $,
$ A_1 $ 表示的数为 $ \frac{0 + 4}{2} = 2 = \frac{4}{2^1} $;
第 $ 2 $ 次跳动到 $ A_1O $ 的中点 $ A_2 $,
$ A_2 $ 表示的数为 $ \frac{0 + 2}{2} = 1 = \frac{4}{2^2} $;
第 $ 3 $ 次跳动到 $ A_2O $ 的中点 $ A_3 $,
$ A_3 $ 表示的数为 $ \frac{0 + 1}{2} = \frac{1}{2} = \frac{4}{2^3} $;
……
依此类推,第 $ n $ 次跳动后,点 $ A_n $ 表示的数为 $ \frac{4}{2^n} $。
线段 $ A_nA $ 的长为点 $ A $ 与点 $ A_n $ 表示的数之差的绝对值,
即 $ |4 - \frac{4}{2^n}| = 4 - \frac{4}{2^n} = 4\left(1 - \frac{1}{2^n}\right) = 4 - \frac{1}{2^{n-2}} $。
故线段 $ A_nA $ 的长为 $ 4 - \frac{1}{2^{n-2}} $。
答案:$ 4 - \frac{1}{2^{n-2}} $
17. 新趋势 推导探究 (2025·江苏常州期末)如图,$ O $ 为原点,在数轴上点 $ A $ 表示的数为 $ a $,点 $ B $ 表示的数为 $ b $,且 $ a $,$ b $ 满足 $ |a + 2| + (3a + b)^2 = 0 $.
(1) 填空:$ a = $
(2) 点 $ P $ 从点 $ A $ 出发,以每秒 1 个单位长度的速度沿数轴向右匀速运动,设运动的时间为 $ t\mathrm{s} $.
① 当点 $ P $ 运动到线段 $ OB $ 上,且 $ OP = 2PB $ 时,求 $ t $ 的值;
② 先取 $ OB $ 的中点 $ E $,当点 $ P $ 在线段 $ OE $ 上时,再取 $ AP $ 的中点 $ F $,则 $ \frac{AB - OP}{EF} $ 的值是否为定值?若是,求出该定值;若不是,请用含 $ t $ 的代数式表示.

(1) 填空:$ a = $
-2
,$ b = $6
;(2) 点 $ P $ 从点 $ A $ 出发,以每秒 1 个单位长度的速度沿数轴向右匀速运动,设运动的时间为 $ t\mathrm{s} $.
① 当点 $ P $ 运动到线段 $ OB $ 上,且 $ OP = 2PB $ 时,求 $ t $ 的值;
② 先取 $ OB $ 的中点 $ E $,当点 $ P $ 在线段 $ OE $ 上时,再取 $ AP $ 的中点 $ F $,则 $ \frac{AB - OP}{EF} $ 的值是否为定值?若是,求出该定值;若不是,请用含 $ t $ 的代数式表示.

(2)①$t=6$;②是定值,定值为$2$
答案:【解析】:本题主要考查了数轴上点的位置关系、绝对值和平方的非负性、动点问题以及线段中点的性质。
(1)已知$\vert a+2\vert+(3a+b)^2=0$。
因为绝对值和平方都具有非负性,即$\vert a+2\vert\geq0$,$(3a+b)^2\geq0$。
要使两个非负数的和为$0$,则这两个非负数必须都为$0$,
可得到方程组$\begin{cases}a+2=0,\\3a+b=0.\end{cases}$
由$a+2=0$,可得$a=-2$。
将$a=-2$代入$3a+b=0$,即$3×(-2)+b=0$,
$-6+b=0$,解得$b=6$。
(2)①由(1)可知$A$点表示的数为$-2$,$B$点表示的数为$6$,
所以$OB=6$,$OA=2$,$AB=6-(-2)=8$。
点$P$从点$A$出发,以每秒$1$个单位长度的速度沿数轴向右匀速运动,运动时间为$t\mathrm{s}$,
则点$P$表示的数为$-2+t$。
因为点$P$在线段$OB$上,所以$0\leq -2+t\leq 6$,解得$2\leq t\leq 8$。
已知$OP = 2PB$,$OP=\vert -2+t\vert=t - 2$(因为$2\leq t\leq 8$,所以$-2+t\geq0$),$PB=6-(-2+t)=8 - t$。
根据$OP = 2PB$可得$t - 2=2×(8 - t)$。
展开括号得$t - 2=16 - 2t$。
移项得$t+2t=16 + 2$。
合并同类项得$3t=18$,解得$t=6$。
②因为$E$是$OB$的中点,$OB=6$,
所以$E$点表示的数为$\frac{0 + 6}{2}=3$。
点$P$表示的数为$-2+t$,$0\leq -2+t\leq 3$,解得$2\leq t\leq 5$。
$AP=t$(点$P$运动的速度为每秒$1$个单位长度,运动时间为$t\mathrm{s}$),
因为$F$是$AP$的中点,所以$AF=\frac{1}{2}t$,
则点$F$表示的数为$-2+\frac{1}{2}t$。
$OP=\vert -2+t\vert=t - 2$(因为$2\leq t\leq 5$,所以$-2+t\geq0$),
$EF=3-(-2+\frac{1}{2}t)=5-\frac{1}{2}t$。
将$AB=8$,$OP=t - 2$,$EF=5-\frac{1}{2}t$代入$\frac{AB - OP}{EF}$可得:
$\frac{8-(t - 2)}{5-\frac{1}{2}t}=\frac{10 - t}{5-\frac{1}{2}t}=\frac{2(5 - \frac{1}{2}t)}{5-\frac{1}{2}t}=2$。
所以$\frac{AB - OP}{EF}$的值是定值,定值为$2$。
【答案】:(1)$a=-2$,$b=6$;(2)①$t=6$;②是定值,定值为$2$。
(1)已知$\vert a+2\vert+(3a+b)^2=0$。
因为绝对值和平方都具有非负性,即$\vert a+2\vert\geq0$,$(3a+b)^2\geq0$。
要使两个非负数的和为$0$,则这两个非负数必须都为$0$,
可得到方程组$\begin{cases}a+2=0,\\3a+b=0.\end{cases}$
由$a+2=0$,可得$a=-2$。
将$a=-2$代入$3a+b=0$,即$3×(-2)+b=0$,
$-6+b=0$,解得$b=6$。
(2)①由(1)可知$A$点表示的数为$-2$,$B$点表示的数为$6$,
所以$OB=6$,$OA=2$,$AB=6-(-2)=8$。
点$P$从点$A$出发,以每秒$1$个单位长度的速度沿数轴向右匀速运动,运动时间为$t\mathrm{s}$,
则点$P$表示的数为$-2+t$。
因为点$P$在线段$OB$上,所以$0\leq -2+t\leq 6$,解得$2\leq t\leq 8$。
已知$OP = 2PB$,$OP=\vert -2+t\vert=t - 2$(因为$2\leq t\leq 8$,所以$-2+t\geq0$),$PB=6-(-2+t)=8 - t$。
根据$OP = 2PB$可得$t - 2=2×(8 - t)$。
展开括号得$t - 2=16 - 2t$。
移项得$t+2t=16 + 2$。
合并同类项得$3t=18$,解得$t=6$。
②因为$E$是$OB$的中点,$OB=6$,
所以$E$点表示的数为$\frac{0 + 6}{2}=3$。
点$P$表示的数为$-2+t$,$0\leq -2+t\leq 3$,解得$2\leq t\leq 5$。
$AP=t$(点$P$运动的速度为每秒$1$个单位长度,运动时间为$t\mathrm{s}$),
因为$F$是$AP$的中点,所以$AF=\frac{1}{2}t$,
则点$F$表示的数为$-2+\frac{1}{2}t$。
$OP=\vert -2+t\vert=t - 2$(因为$2\leq t\leq 5$,所以$-2+t\geq0$),
$EF=3-(-2+\frac{1}{2}t)=5-\frac{1}{2}t$。
将$AB=8$,$OP=t - 2$,$EF=5-\frac{1}{2}t$代入$\frac{AB - OP}{EF}$可得:
$\frac{8-(t - 2)}{5-\frac{1}{2}t}=\frac{10 - t}{5-\frac{1}{2}t}=\frac{2(5 - \frac{1}{2}t)}{5-\frac{1}{2}t}=2$。
所以$\frac{AB - OP}{EF}$的值是定值,定值为$2$。
【答案】:(1)$a=-2$,$b=6$;(2)①$t=6$;②是定值,定值为$2$。