10. 如图,直线AB,CD相交于点O.若∠AOC= 75°,∠1= 25°,则∠2的度数是(
A.25°
B.30°
C.40°
D.50°
D
)A.25°
B.30°
C.40°
D.50°
答案:【解析】:
本题可根据对顶角的性质求出$∠BOD$的度数,再结合$∠1$的度数,利用$∠2$与$∠BOD$、$∠1$的关系求出$∠2$的度数,考查了学生对对顶角性质的理解和运用能力。
已知$∠AOC = 75°$,因为对顶角相等,$∠AOC$与$∠BOD$是对顶角,所以$∠BOD=∠AOC = 75°$。
又已知$∠1 = 25°$,观察图形可知$∠BOD=∠1 + ∠2$,那么$∠2=∠BOD - ∠1$。
将$∠BOD = 75°$,$∠1 = 25°$代入$∠2=∠BOD - ∠1$,可得$∠2 = 75° - 25° = 50°$。
【答案】:D
本题可根据对顶角的性质求出$∠BOD$的度数,再结合$∠1$的度数,利用$∠2$与$∠BOD$、$∠1$的关系求出$∠2$的度数,考查了学生对对顶角性质的理解和运用能力。
已知$∠AOC = 75°$,因为对顶角相等,$∠AOC$与$∠BOD$是对顶角,所以$∠BOD=∠AOC = 75°$。
又已知$∠1 = 25°$,观察图形可知$∠BOD=∠1 + ∠2$,那么$∠2=∠BOD - ∠1$。
将$∠BOD = 75°$,$∠1 = 25°$代入$∠2=∠BOD - ∠1$,可得$∠2 = 75° - 25° = 50°$。
【答案】:D
11. 如图,为了把小河中的水引到点C处,可过点C画CD⊥AB于点D,然后沿CD开渠,这样做可使所开的渠道最短,这种设计的依据是
垂线段最短
.答案:【解析】:
本题主要考查垂线段最短定理的应用。
根据垂线段公理:连接直线外一点与直线上各点的所有线段中,垂线段最短。
在这个问题中,点$C$是直线$AB$(代表小河)外的一点,为了把小河中的水引到$C$处,需要找到一条从$C$到$AB$的最短路径。
根据垂线段公理,可以过点$C$作$AB$的垂线,垂足为$D$,这样$CD$就是从$C$到$AB$的最短路径。
因此,这种设计的依据是垂线段最短。
【答案】:
垂线段最短。
本题主要考查垂线段最短定理的应用。
根据垂线段公理:连接直线外一点与直线上各点的所有线段中,垂线段最短。
在这个问题中,点$C$是直线$AB$(代表小河)外的一点,为了把小河中的水引到$C$处,需要找到一条从$C$到$AB$的最短路径。
根据垂线段公理,可以过点$C$作$AB$的垂线,垂足为$D$,这样$CD$就是从$C$到$AB$的最短路径。
因此,这种设计的依据是垂线段最短。
【答案】:
垂线段最短。
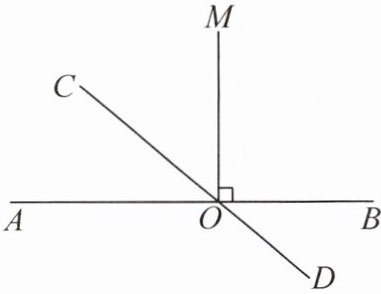
12. 新素养几何直观 如图,直线AB,CD相交于点O,OM⊥AB.若∠AOC= 40°,求∠DOM的度数.

答案:解:因为直线AB,CD相交于点O,∠AOC=40°,
所以∠BOD=∠AOC=40°(对顶角相等)。
因为OM⊥AB,
所以∠MOB=90°(垂直的定义)。
所以∠DOM=∠MOB+∠BOD=90°+40°=130°。
答:∠DOM的度数为130°。
所以∠BOD=∠AOC=40°(对顶角相等)。
因为OM⊥AB,
所以∠MOB=90°(垂直的定义)。
所以∠DOM=∠MOB+∠BOD=90°+40°=130°。
答:∠DOM的度数为130°。
13. (2024·四川甘孜)如图,AB//CD,AD平分∠BAC,∠1= 30°,则∠2的度数为(

A.15°
B.30°
C.45°
D.60°
D
)
A.15°
B.30°
C.45°
D.60°
答案:解:∵AB//CD,∠1=30°,
∴∠BAD=∠1=30°(两直线平行,内错角相等)。
∵AD平分∠BAC,
∴∠BAC=2∠BAD=60°。
∵AB//CD,
∴∠2=∠BAC=60°(两直线平行,内错角相等)。
答案:D
∴∠BAD=∠1=30°(两直线平行,内错角相等)。
∵AD平分∠BAC,
∴∠BAC=2∠BAD=60°。
∵AB//CD,
∴∠2=∠BAC=60°(两直线平行,内错角相等)。
答案:D
14. 如图,已知AB//FE//DC,AF//ED//BC,∠B= 65°,则∠F+∠D等于(
A.130°
B.120°
C.115°
D.90°
A
)A.130°
B.120°
C.115°
D.90°
答案:解:∵AB//FE//DC,AF//ED//BC,
∴四边形ABEF、四边形EFCD、四边形ABCD均为平行四边形(两组对边分别平行的四边形是平行四边形)。
∵四边形ABEF是平行四边形,∠B=65°,
∴∠F=∠B=65°(平行四边形的对角相等)。
∵四边形EFCD是平行四边形,
∴∠D=∠F=65°(平行四边形的对角相等)。
∴∠F+∠D=65°+65°=130°。
答案:A
∴四边形ABEF、四边形EFCD、四边形ABCD均为平行四边形(两组对边分别平行的四边形是平行四边形)。
∵四边形ABEF是平行四边形,∠B=65°,
∴∠F=∠B=65°(平行四边形的对角相等)。
∵四边形EFCD是平行四边形,
∴∠D=∠F=65°(平行四边形的对角相等)。
∴∠F+∠D=65°+65°=130°。
答案:A
15. 新素养推理能力 如图,已知∠1+∠2= 180°,∠A= ∠C,DA平分∠BDF.试说明:
(1) AD//BC;
(2) BC平分∠DBE.

(1) AD//BC;
(2) BC平分∠DBE.

答案:(1)解:∵∠1+∠2=180°,∠1=∠ABD,∠2=∠BDC,
∴∠ABD+∠BDC=180°,
∴AB//FC,
∴∠A=∠ADF,
∵∠A=∠C,
∴∠ADF=∠C,
∴AD//BC;
(2)解:∵AD//BC,
∴∠ADB=∠DBC,∠DAF=∠C,
∵DA平分∠BDF,
∴∠ADB=∠ADF,
∵∠A=∠C,∠DAF=∠C,
∴∠A=∠DAF,
∵AB//FC,
∴∠A=∠ADF,
∴∠ADF=∠DAF=∠A=∠C,
∵∠ADF=∠C,∠ADB=∠DBC,∠ADB=∠ADF,
∴∠DBC=∠C,
∵AB//FC,
∴∠EBC=∠C,
∴∠DBC=∠EBC,
∴BC平分∠DBE.
∴∠ABD+∠BDC=180°,
∴AB//FC,
∴∠A=∠ADF,
∵∠A=∠C,
∴∠ADF=∠C,
∴AD//BC;
(2)解:∵AD//BC,
∴∠ADB=∠DBC,∠DAF=∠C,
∵DA平分∠BDF,
∴∠ADB=∠ADF,
∵∠A=∠C,∠DAF=∠C,
∴∠A=∠DAF,
∵AB//FC,
∴∠A=∠ADF,
∴∠ADF=∠DAF=∠A=∠C,
∵∠ADF=∠C,∠ADB=∠DBC,∠ADB=∠ADF,
∴∠DBC=∠C,
∵AB//FC,
∴∠EBC=∠C,
∴∠DBC=∠EBC,
∴BC平分∠DBE.
16. 下列图形中,属于多边形的是(
C
)答案:【解析】:本题考查多边形的定义,根据多边形的定义:平面内不在同一条直线上的几条线段首尾顺次相接组成的图形叫做多边形。对选项逐一分析,A选项是一个圆,不是由线段首尾顺次相接组成,不符合多边形定义;B选项是一个扇形,也不是由线段首尾顺次相接组成,不符合多边形定义;C选项是一个四边形,由四条线段首尾顺次相接组成,符合多边形定义;D选项是一条线段和一个射线组成的图形,不是由线段首尾顺次相接组成,不符合多边形定义。
【答案】:C
【答案】:C
17. 如图,从五边形纸片ABCDE中沿虚线剪去一个三角形得到六边形ABCDGF,则该六边形的周长一定比原五边形的周长小,理由为
两点之间,线段最短
.答案:解:两点之间,线段最短。