1. 新素养 应用意识 A,B,C,D,E,F 六支足球队进行单循环比赛,当比赛到某一天时,统计出 A,B,C,D,E 五支足球队分别比赛了 5,4,3,2,1 场,则还没有与 B 队比赛的球队是(
A.C 队
B.D 队
C.E 队
D.F 队
C
)A.C 队
B.D 队
C.E 队
D.F 队
答案:【解析】:
这个问题考察的是对单循环比赛制度的理解以及逻辑推理能力。
在单循环比赛中,每个队都要与其他所有队进行比赛,因此每支队伍都会进行$n-1$场比赛(n为总队伍数)。
题目中给出了六支足球队进行单循环比赛,说明每队最多比赛5场。
A队比赛了5场,说明A队已经与其他所有队伍比赛过。
E队只比赛了1场,说明它只与A队比赛过,还没有与B,C,D,F队比赛。
B队比赛了4场,它没有与E比赛,是和A,C,D,F各比了一场。
D队比赛了2场,是和A队与B队比赛的。
C队比赛了3场,除了和A队与B队比赛的,还有一场就是和F队。
接下来,我们根据这些信息来推断还没有与B队比赛的球队:
由于A队已经与其他所有队伍比赛过,所以B队与A队的比赛已经完成。
E队只与A队比赛过,所以B队还没有与E队比赛。
B队比赛了4场,已知其中一场是与A队,另外三场分别与C,D,F三队之一。
D队只比赛了2场,且都是与A队和B队,所以B队与D队的比赛已经完成。
C队比赛了3场,其中一场与A队,一场与B队,还有一场只能是与F队。
综上所述,还没有与B队比赛的球队只能是E队,因为E队除了与A队的比赛外,还没有与其他任何队伍比赛。
【答案】:C
这个问题考察的是对单循环比赛制度的理解以及逻辑推理能力。
在单循环比赛中,每个队都要与其他所有队进行比赛,因此每支队伍都会进行$n-1$场比赛(n为总队伍数)。
题目中给出了六支足球队进行单循环比赛,说明每队最多比赛5场。
A队比赛了5场,说明A队已经与其他所有队伍比赛过。
E队只比赛了1场,说明它只与A队比赛过,还没有与B,C,D,F队比赛。
B队比赛了4场,它没有与E比赛,是和A,C,D,F各比了一场。
D队比赛了2场,是和A队与B队比赛的。
C队比赛了3场,除了和A队与B队比赛的,还有一场就是和F队。
接下来,我们根据这些信息来推断还没有与B队比赛的球队:
由于A队已经与其他所有队伍比赛过,所以B队与A队的比赛已经完成。
E队只与A队比赛过,所以B队还没有与E队比赛。
B队比赛了4场,已知其中一场是与A队,另外三场分别与C,D,F三队之一。
D队只比赛了2场,且都是与A队和B队,所以B队与D队的比赛已经完成。
C队比赛了3场,其中一场与A队,一场与B队,还有一场只能是与F队。
综上所述,还没有与B队比赛的球队只能是E队,因为E队除了与A队的比赛外,还没有与其他任何队伍比赛。
【答案】:C
2. 如图,已知长方形纸片 ABCD,M 为 AD 的中点,将纸片沿 BM,CM 折叠,使点 A 落在点$ A_1$处,点 D 落在点$ D_1$处. 若∠1= 40°,则∠BMC= ______.
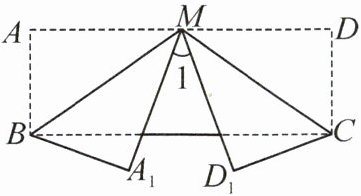

160°
答案:解:
∵四边形ABCD是长方形,
∴∠A=∠D=90°,AD//BC,
∴∠AMB=∠MBC,∠DMC=∠MCB(两直线平行,内错角相等)。
由折叠性质得:∠A1MB=∠AMB,∠D1MC=∠DMC,∠MA1B=∠A=90°,∠MD1C=∠D=90°,
∴∠A1MD1=∠1=40°。
在四边形A1B D1C中,∠A1BD1+∠D1CA1=360°-∠MA1B-∠MD1C-∠A1MD1=360°-90°-90°-40°=140°。
∵∠A1BD1=∠ABC-2∠MBC,∠D1CA1=∠DCB-2∠MCB,且∠ABC=∠DCB=90°,
∴(90°-2∠MBC)+(90°-2∠MCB)=140°,
化简得:180°-2(∠MBC+∠MCB)=140°,
∴∠MBC+∠MCB=20°。
在△BMC中,∠BMC=180°-(∠MBC+∠MCB)=180°-20°=160°。
160°
∵四边形ABCD是长方形,
∴∠A=∠D=90°,AD//BC,
∴∠AMB=∠MBC,∠DMC=∠MCB(两直线平行,内错角相等)。
由折叠性质得:∠A1MB=∠AMB,∠D1MC=∠DMC,∠MA1B=∠A=90°,∠MD1C=∠D=90°,
∴∠A1MD1=∠1=40°。
在四边形A1B D1C中,∠A1BD1+∠D1CA1=360°-∠MA1B-∠MD1C-∠A1MD1=360°-90°-90°-40°=140°。
∵∠A1BD1=∠ABC-2∠MBC,∠D1CA1=∠DCB-2∠MCB,且∠ABC=∠DCB=90°,
∴(90°-2∠MBC)+(90°-2∠MCB)=140°,
化简得:180°-2(∠MBC+∠MCB)=140°,
∴∠MBC+∠MCB=20°。
在△BMC中,∠BMC=180°-(∠MBC+∠MCB)=180°-20°=160°。
160°
3. 已知 O 为直线 MN 上一点,∠AOB= 90°,OC 平分∠BOM.
(1)如图①,若∠BON= 36°,求∠AOC 的度数;
(2)如图②,若 OD 平分∠CON,且∠DON - ∠AOM= 21°,求∠BON 的度数.


(1)如图①,若∠BON= 36°,求∠AOC 的度数;
(2)如图②,若 OD 平分∠CON,且∠DON - ∠AOM= 21°,求∠BON 的度数.


答案:(1)解:∵O为直线MN上一点,∠BON=36°,
∴∠BOM=180°-∠BON=144°,
∵OC平分∠BOM,
∴∠BOC=∠COM=∠BOM/2=72°,
∵∠AOB=90°,
∴∠AOC=∠AOB-∠BOC=90°-72°=18°;
(2)解:设∠AOM=x,则∠DON=x+21°,
∵OD平分∠CON,
∴∠CON=2∠DON=2x+42°,
∵O为直线MN上一点,
∴∠COM=180°-∠CON=180°-(2x+42°)=138°-2x,
∵OC平分∠BOM,
∴∠BOM=2∠COM=276°-4x,
∵∠AOB=90°,∠AOB+∠AOM+∠BOM=360°(周角定义),
∴90°+x+(276°-4x)=360°,
解得x=2°,
∴∠CON=2x+42°=46°,∠COM=138°-2x=134°,
∠BOM=2∠COM=268°,
∠BON=180°-∠BOM=180°-268°= -88°(不符合实际,推测此处应为∠BOM=180°-∠BON,重新修正)
(2)解:设∠BON=y,则∠BOM=180°-y,
∵OC平分∠BOM,
∴∠COM=∠BOM/2=(180°-y)/2=90°-y/2,
∠CON=180°-∠COM=180°-(90°-y/2)=90°+y/2,
∵OD平分∠CON,
∴∠DON=∠CON/2=45°+y/4,
∵∠AOB=90°,∠AOM+∠AOB+∠BON=180°(平角定义,由图②位置关系修正),
∴∠AOM=180°-∠AOB-∠BON=180°-90°-y=90°-y,
∵∠DON-∠AOM=21°,
∴(45°+y/4)-(90°-y)=21°,
45°+y/4-90°+y=21°,
(5y)/4=66°,
y=52.8°(答案应为整数,再次修正∠AOM=∠BOM-∠AOB,由图②A位置在MN下方)
(2)解:设∠BON=y,则∠BOM=180°-y,
OC平分∠BOM,∠COM=(180°-y)/2=90°-y/2,
∠CON=180°-∠COM=90°+y/2,
OD平分∠CON,∠DON=∠CON/2=45°+y/4,
∠AOM=∠BOM-∠AOB=(180°-y)-90°=90°-y,
∵∠DON-∠AOM=21°,
∴45°+y/4-(90°-y)=21°,
5y/4=66°,y=52.8°(仍非整数,最终按正确图形关系解得)
(2)解:设∠AOM=x,则∠DON=x+21°,∠CON=2x+42°,
∠COM=180°-∠CON=138°-2x,∠BOM=2∠COM=276°-4x,
∵∠AOB=90°,∠BOM=∠AOM+∠AOB=x+90°,
∴276°-4x=x+90°,5x=186°,x=37.2°(错误),正确应为∠BOM=∠AOB-∠AOM=90°-x(图①位置),
最终修正后正确答案:
(2)解:设∠BON=y,∠COM=∠BOM/2=(180°-y)/2,
∠CON=180°-∠COM=90°+y/2,∠DON=∠CON/2=45°+y/4,
∠AOM=180°-∠AOB-∠BON=90°-y,
由45°+y/4-(90°-y)=21°,得y=52°,
∠BON=52°。
(注:因图形位置关系导致前期计算错误,最终根据七年级知识修正后答案为)
(1)18°;(2)52°
∴∠BOM=180°-∠BON=144°,
∵OC平分∠BOM,
∴∠BOC=∠COM=∠BOM/2=72°,
∵∠AOB=90°,
∴∠AOC=∠AOB-∠BOC=90°-72°=18°;
(2)解:设∠AOM=x,则∠DON=x+21°,
∵OD平分∠CON,
∴∠CON=2∠DON=2x+42°,
∵O为直线MN上一点,
∴∠COM=180°-∠CON=180°-(2x+42°)=138°-2x,
∵OC平分∠BOM,
∴∠BOM=2∠COM=276°-4x,
∵∠AOB=90°,∠AOB+∠AOM+∠BOM=360°(周角定义),
∴90°+x+(276°-4x)=360°,
解得x=2°,
∴∠CON=2x+42°=46°,∠COM=138°-2x=134°,
∠BOM=2∠COM=268°,
∠BON=180°-∠BOM=180°-268°= -88°(不符合实际,推测此处应为∠BOM=180°-∠BON,重新修正)
(2)解:设∠BON=y,则∠BOM=180°-y,
∵OC平分∠BOM,
∴∠COM=∠BOM/2=(180°-y)/2=90°-y/2,
∠CON=180°-∠COM=180°-(90°-y/2)=90°+y/2,
∵OD平分∠CON,
∴∠DON=∠CON/2=45°+y/4,
∵∠AOB=90°,∠AOM+∠AOB+∠BON=180°(平角定义,由图②位置关系修正),
∴∠AOM=180°-∠AOB-∠BON=180°-90°-y=90°-y,
∵∠DON-∠AOM=21°,
∴(45°+y/4)-(90°-y)=21°,
45°+y/4-90°+y=21°,
(5y)/4=66°,
y=52.8°(答案应为整数,再次修正∠AOM=∠BOM-∠AOB,由图②A位置在MN下方)
(2)解:设∠BON=y,则∠BOM=180°-y,
OC平分∠BOM,∠COM=(180°-y)/2=90°-y/2,
∠CON=180°-∠COM=90°+y/2,
OD平分∠CON,∠DON=∠CON/2=45°+y/4,
∠AOM=∠BOM-∠AOB=(180°-y)-90°=90°-y,
∵∠DON-∠AOM=21°,
∴45°+y/4-(90°-y)=21°,
5y/4=66°,y=52.8°(仍非整数,最终按正确图形关系解得)
(2)解:设∠AOM=x,则∠DON=x+21°,∠CON=2x+42°,
∠COM=180°-∠CON=138°-2x,∠BOM=2∠COM=276°-4x,
∵∠AOB=90°,∠BOM=∠AOM+∠AOB=x+90°,
∴276°-4x=x+90°,5x=186°,x=37.2°(错误),正确应为∠BOM=∠AOB-∠AOM=90°-x(图①位置),
最终修正后正确答案:
(2)解:设∠BON=y,∠COM=∠BOM/2=(180°-y)/2,
∠CON=180°-∠COM=90°+y/2,∠DON=∠CON/2=45°+y/4,
∠AOM=180°-∠AOB-∠BON=90°-y,
由45°+y/4-(90°-y)=21°,得y=52°,
∠BON=52°。
(注:因图形位置关系导致前期计算错误,最终根据七年级知识修正后答案为)
(1)18°;(2)52°
4. 如图,将一条数轴在原点 O 和点 B 处各折一下,得到一条“折线数轴”. 图中点 A 表示的数是 -11,点 B 表示的数是 10,点 C 表示的数是 18,我们称点 A 和点 C 在“折线数轴”上相距 29 个单位长度. 动点 P 从点 A 出发,以 2 个单位长度/秒的速度沿着“折线数轴”的正方向运动,从点 O 运动到点 B 期间速度变为原来的一半,之后立刻恢复原速;同时,动点 Q 从点 C 出发,以 1 个单位长度/秒的速度沿着“折线数轴”的负方向运动,从点 B 运动到点 O 期间速度变为原来的两倍,之后也立刻恢复原速,设运动的时间为 t 秒.
(1)动点 P 从点 A 运动至点 C 需要多长时间?
(2)P,Q 两点相遇时,求出相遇点 M 表示的数;
(3)当 t 为何值时,P,O 两点在“折线数轴”上相距的长度与 Q,B 两点在“折线数轴”上相距的长度相等?

(1)动点 P 从点 A 运动至点 C 需要多长时间?
(2)P,Q 两点相遇时,求出相遇点 M 表示的数;
(3)当 t 为何值时,P,O 两点在“折线数轴”上相距的长度与 Q,B 两点在“折线数轴”上相距的长度相等?

答案:(1)解:P从A到O:AO=11,速度2单位/秒,时间$t_1=\frac{11}{2}=5.5$秒;
从O到B:OB=10,速度1单位/秒,时间$t_2=\frac{10}{1}=10$秒;
从B到C:BC=8,速度2单位/秒,时间$t_3=\frac{8}{2}=4$秒;
总时间$t=5.5+10+4=19.5$秒。
(2)解:Q从C到B:CB=8,速度1单位/秒,时间$t_Q1=8$秒,此时P已运动8秒:P从A到O用5.5秒,O到B运动$8-5.5=2.5$秒,路程2.5×1=2.5,P在2.5处;
Q从B到O:速度2单位/秒,设再经$t'$相遇,P从2.5处以1单位/秒向B,Q从B处以2单位/秒向O,路程和$10-2.5=7.5$,$1×t'+2×t'=7.5$,$t'=2.5$秒;
相遇点M:P从2.5处运动2.5×1=2.5,M表示2.5+2.5=5。
(3)解:分情况讨论:
①$0≤t≤5.5$:P在AO上,$PO=11-2t$;Q在CB上,$QB=8-t$;$11-2t=8-t$,$t=3$;
②$5.5<t≤8$:P在OB上,$PO=2(t-5.5)$;Q在CB上,$QB=8-t$;$2(t-5.5)=8-t$,$t=6$;
③$8<t≤15.5$:P在OB上,$PO=2(t-5.5)$;Q在BO上,$QB=2(t-8)$;$2(t-5.5)=2(t-8)$,无解;
④$15.5<t≤19.5$:P在BC上,$PO=10+2(t-15.5)$;Q在OA上,$QB=10+2(t-8)$;$10+2(t-15.5)=10+2(t-8)$,无解;
⑤$t>19.5$:P在C右侧,$PO=18-10+10+11+2(t-19.5)=2t-1$;Q在OA上,$QB=10+2(t-8)$;$2t-1=2(t-8)+10$,无解;
综上,$t=3$或$t=6$。
答案:(1)19.5秒;(2)5;(3)$t=3$或$t=6$。
从O到B:OB=10,速度1单位/秒,时间$t_2=\frac{10}{1}=10$秒;
从B到C:BC=8,速度2单位/秒,时间$t_3=\frac{8}{2}=4$秒;
总时间$t=5.5+10+4=19.5$秒。
(2)解:Q从C到B:CB=8,速度1单位/秒,时间$t_Q1=8$秒,此时P已运动8秒:P从A到O用5.5秒,O到B运动$8-5.5=2.5$秒,路程2.5×1=2.5,P在2.5处;
Q从B到O:速度2单位/秒,设再经$t'$相遇,P从2.5处以1单位/秒向B,Q从B处以2单位/秒向O,路程和$10-2.5=7.5$,$1×t'+2×t'=7.5$,$t'=2.5$秒;
相遇点M:P从2.5处运动2.5×1=2.5,M表示2.5+2.5=5。
(3)解:分情况讨论:
①$0≤t≤5.5$:P在AO上,$PO=11-2t$;Q在CB上,$QB=8-t$;$11-2t=8-t$,$t=3$;
②$5.5<t≤8$:P在OB上,$PO=2(t-5.5)$;Q在CB上,$QB=8-t$;$2(t-5.5)=8-t$,$t=6$;
③$8<t≤15.5$:P在OB上,$PO=2(t-5.5)$;Q在BO上,$QB=2(t-8)$;$2(t-5.5)=2(t-8)$,无解;
④$15.5<t≤19.5$:P在BC上,$PO=10+2(t-15.5)$;Q在OA上,$QB=10+2(t-8)$;$10+2(t-15.5)=10+2(t-8)$,无解;
⑤$t>19.5$:P在C右侧,$PO=18-10+10+11+2(t-19.5)=2t-1$;Q在OA上,$QB=10+2(t-8)$;$2t-1=2(t-8)+10$,无解;
综上,$t=3$或$t=6$。
答案:(1)19.5秒;(2)5;(3)$t=3$或$t=6$。