1. (2024·四川成都)-5的绝对值是(
A.5
B.-5
C.$\frac{1}{5}$
D.$-\frac{1}{5}$
A
)A.5
B.-5
C.$\frac{1}{5}$
D.$-\frac{1}{5}$
答案:【解析】:
本题考查绝对值的定义。绝对值表示一个数距离0的远近,因此任何数的绝对值都是非负的。对于给定的数-5,其绝对值表示为$|-5|$。
根据绝对值的定义,若$x$为非负数,则$|x| = x$;若$x$为负数,则$|x| = -x$。
因此,对于-5,其绝对值为$|-5| = -(-5) = 5$。
【答案】:
A. 5
本题考查绝对值的定义。绝对值表示一个数距离0的远近,因此任何数的绝对值都是非负的。对于给定的数-5,其绝对值表示为$|-5|$。
根据绝对值的定义,若$x$为非负数,则$|x| = x$;若$x$为负数,则$|x| = -x$。
因此,对于-5,其绝对值为$|-5| = -(-5) = 5$。
【答案】:
A. 5
2. 在数轴上,表示-5,$\left|-2 \frac{1}{3}\right|$,0,0.125,$\frac{7}{4}$,$\left|-\frac{5}{6}\right|$的点中,在原点右侧的有(
A.1个
B.2个
C.3个
D.4个
D
)A.1个
B.2个
C.3个
D.4个
答案:【解析】:
题目要求确定在数轴上哪些点位于原点的右侧,即确定哪些数是正数。给定的数包括负数、零、正分数、绝对值表达式等。需要先计算或确定每个数的具体值,再判断其是否为正数。
$-5$ 是一个负数,所以在原点的左侧。
$\left|-2 \frac{1}{3}\right|$ 的绝对值是 $2 \frac{1}{3}$,这是一个正数,所以在原点的右侧。
$0$ 既不是正数也不是负数,所以不在原点的右侧。
$0.125$ 是一个正数,所以在原点的右侧。
$\frac{7}{4}$ 是一个正数,所以在原点的右侧。
$\left|-\frac{5}{6}\right|$ 的绝对值是 $\frac{5}{6}$,这是一个正数,所以在原点的右侧。
综上所述,在原点右侧的点有4个。
【答案】:
D.4个
题目要求确定在数轴上哪些点位于原点的右侧,即确定哪些数是正数。给定的数包括负数、零、正分数、绝对值表达式等。需要先计算或确定每个数的具体值,再判断其是否为正数。
$-5$ 是一个负数,所以在原点的左侧。
$\left|-2 \frac{1}{3}\right|$ 的绝对值是 $2 \frac{1}{3}$,这是一个正数,所以在原点的右侧。
$0$ 既不是正数也不是负数,所以不在原点的右侧。
$0.125$ 是一个正数,所以在原点的右侧。
$\frac{7}{4}$ 是一个正数,所以在原点的右侧。
$\left|-\frac{5}{6}\right|$ 的绝对值是 $\frac{5}{6}$,这是一个正数,所以在原点的右侧。
综上所述,在原点右侧的点有4个。
【答案】:
D.4个
3. 新素养 几何直观 已知M,N,P,Q四点在数轴上的位置如图所示,其中表示的数的绝对值最大的点是(
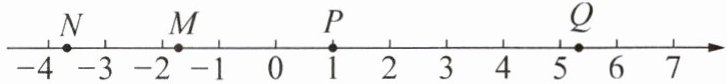
A.点M
B.点N
C.点P
D.点Q
D
)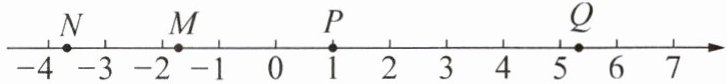
A.点M
B.点N
C.点P
D.点Q
答案:【解析】:
此题主要考查了绝对值的定义以及数轴的应用。
首先,需要理解绝对值的定义:一个数在数轴上所对应点到原点的距离叫做这个数的绝对值。
接下来,根据题目中给出的数轴和各点的位置,可以确定每个点到原点的距离。
点$M$位于$-1$和$-2$之间,其绝对值小于$2$;
点$N$位于$-3$和$-4$之间,其绝对值大于$3$且小于$4$;
点$P$位于$0$和$2$之间,其绝对值小于$2$;
点$Q$位于$5$和$6$之间,其绝对值大于$5$且小于$6$。
通过比较,可以明显看出点$Q$到原点的距离最远,因此其绝对值最大。
【答案】:
D.点$Q$。
此题主要考查了绝对值的定义以及数轴的应用。
首先,需要理解绝对值的定义:一个数在数轴上所对应点到原点的距离叫做这个数的绝对值。
接下来,根据题目中给出的数轴和各点的位置,可以确定每个点到原点的距离。
点$M$位于$-1$和$-2$之间,其绝对值小于$2$;
点$N$位于$-3$和$-4$之间,其绝对值大于$3$且小于$4$;
点$P$位于$0$和$2$之间,其绝对值小于$2$;
点$Q$位于$5$和$6$之间,其绝对值大于$5$且小于$6$。
通过比较,可以明显看出点$Q$到原点的距离最远,因此其绝对值最大。
【答案】:
D.点$Q$。
4. (2024·江苏镇江)-100的绝对值为
100
.答案:【解析】:
本题考查绝对值的定义。绝对值表示一个数到0的距离,因此任何数的绝对值都是非负的。对于负数,其绝对值等于它的相反数。
【答案】:
$|-100| = 100$
所以,$-100$的绝对值为$100$。
本题考查绝对值的定义。绝对值表示一个数到0的距离,因此任何数的绝对值都是非负的。对于负数,其绝对值等于它的相反数。
【答案】:
$|-100| = 100$
所以,$-100$的绝对值为$100$。
5. 绝对值不大于2的整数有
5
个,它们是$\pm 2$,$\pm 1$,0
.答案:【解析】:
题目考查绝对值的概念及性质。绝对值的定义是一个数到0的距离,所以绝对值不大于2,即这个数到0的距离不大于2,可以是在-2到2之间的所有整数。
首先,考虑正整数部分,有1和2满足条件;
其次,0的绝对值也是0,小于2,所以0也满足条件;
最后,考虑负整数部分,由于绝对值的性质,-1和-2也满足条件。
综上,绝对值不大于2的整数有:-2,-1,0,1,2。
【答案】:
5;$\pm 2$,$\pm 1$,0。
题目考查绝对值的概念及性质。绝对值的定义是一个数到0的距离,所以绝对值不大于2,即这个数到0的距离不大于2,可以是在-2到2之间的所有整数。
首先,考虑正整数部分,有1和2满足条件;
其次,0的绝对值也是0,小于2,所以0也满足条件;
最后,考虑负整数部分,由于绝对值的性质,-1和-2也满足条件。
综上,绝对值不大于2的整数有:-2,-1,0,1,2。
【答案】:
5;$\pm 2$,$\pm 1$,0。
6. 若M,N两点在数轴上表示的数分别是a,b,且$|a|= 2,|b|= 3$,则M,N两点之间的距离为
1或5
.答案:【解析】:
本题主要考察绝对值的定义以及数轴上两点间的距离公式。
首先,根据绝对值的定义,有 $|a| = 2$,则 $a$ 可以取 $\pm 2$;
同样,$|b| = 3$,则 $b$ 可以取 $\pm 3$。
接下来,我们需要考虑 $M, N$ 两点在数轴上的所有可能位置,并计算它们之间的距离。
当 $a = 2, b = 3$ 时,$M, N$ 两点之间的距离为 $|3 - 2| = 1$;
当 $a = 2, b = -3$ 时,$M, N$ 两点之间的距离为 $|-3 - 2| = 5$;
当 $a = -2, b = 3$ 时,$M, N$ 两点之间的距离为 $|3 - (-2)| = 5$;
当 $a = -2, b = -3$ 时,$M, N$ 两点之间的距离为 $|-3 - (-2)| = 1$。
综上所述,$M, N$ 两点之间的距离可以是 $1$ 或 $5$。
【答案】:
$1$或$5$
本题主要考察绝对值的定义以及数轴上两点间的距离公式。
首先,根据绝对值的定义,有 $|a| = 2$,则 $a$ 可以取 $\pm 2$;
同样,$|b| = 3$,则 $b$ 可以取 $\pm 3$。
接下来,我们需要考虑 $M, N$ 两点在数轴上的所有可能位置,并计算它们之间的距离。
当 $a = 2, b = 3$ 时,$M, N$ 两点之间的距离为 $|3 - 2| = 1$;
当 $a = 2, b = -3$ 时,$M, N$ 两点之间的距离为 $|-3 - 2| = 5$;
当 $a = -2, b = 3$ 时,$M, N$ 两点之间的距离为 $|3 - (-2)| = 5$;
当 $a = -2, b = -3$ 时,$M, N$ 两点之间的距离为 $|-3 - (-2)| = 1$。
综上所述,$M, N$ 两点之间的距离可以是 $1$ 或 $5$。
【答案】:
$1$或$5$
7. (教材P24练习1变式)在数轴上画出表示下列各数的点:$-3,-\frac{1}{2},0,\frac{3}{4},2.5$,并求出这些数的绝对值.


答案:【解析】:
本题主要考查了绝对值的定义,即数轴上某个数与原点的距离叫做这个数的绝对值,以及如何在数轴上表示数。
对于给出的每个数,我们需要首先在数轴上找到对应的位置,然后计算其绝对值。
数轴的绘制:根据数轴的三要素(原点、正方向、单位长度),我们可以绘制出数轴,并在数轴上标出给定的各个数。
绝对值的计算:对于每个给定的数,我们使用绝对值的定义来计算其绝对值。
【答案】:
在数轴上,从左到右依次画出表示$-3$,$-\frac{1}{2}$,$0$,$\frac{3}{4}$,$2.5$的点(图略);
这些数的绝对值分别为:
$|-3| = 3$,
$\left|-\frac{1}{2}\right| = \frac{1}{2}$,
$|0| = 0$,
$\left|\frac{3}{4}\right| = \frac{3}{4}$,
$|2.5| = 2.5$。
本题主要考查了绝对值的定义,即数轴上某个数与原点的距离叫做这个数的绝对值,以及如何在数轴上表示数。
对于给出的每个数,我们需要首先在数轴上找到对应的位置,然后计算其绝对值。
数轴的绘制:根据数轴的三要素(原点、正方向、单位长度),我们可以绘制出数轴,并在数轴上标出给定的各个数。
绝对值的计算:对于每个给定的数,我们使用绝对值的定义来计算其绝对值。
【答案】:
在数轴上,从左到右依次画出表示$-3$,$-\frac{1}{2}$,$0$,$\frac{3}{4}$,$2.5$的点(图略);
这些数的绝对值分别为:
$|-3| = 3$,
$\left|-\frac{1}{2}\right| = \frac{1}{2}$,
$|0| = 0$,
$\left|\frac{3}{4}\right| = \frac{3}{4}$,
$|2.5| = 2.5$。
8. 新素养 运算能力 计算:
(1)$\left|-\frac{2}{3}\right| ÷\left|+\frac{14}{3}\right|$;
(2)$|-3| ×|-6|-|-7| ×|+2|$.
(1)$\left|-\frac{2}{3}\right| ÷\left|+\frac{14}{3}\right|$;
(2)$|-3| ×|-6|-|-7| ×|+2|$.
答案:【解析】:
本题主要考察绝对值的定义及有理数的乘除法运算。
对于绝对值,我们有以下定义:
如果 $a > 0$,则 $|a| = a$
如果 $a = 0$,则 $|a| = 0$
如果 $a < 0$,则 $|a| = -a$
根据这些定义,我们可以计算出每个绝对值的值,然后进行有理数的乘除法运算。
【答案】:
(1)
解:
首先,我们计算两个数的绝对值:
$\left|-\frac{2}{3}\right| = \frac{2}{3}$
$\left|+\frac{14}{3}\right| = \frac{14}{3}$
然后,我们进行除法运算:
$\frac{2}{3} ÷ \frac{14}{3} = \frac{2}{3} × \frac{3}{14} = \frac{1}{7}$
(2)
解:
首先,我们计算各个数的绝对值:
$|-3| = 3$
$|-6| = 6$
$|-7| = 7$
$|+2| = 2$
然后,我们进行乘法和减法运算:
$3 × 6 - 7 × 2 = 18 - 14 = 4$
本题主要考察绝对值的定义及有理数的乘除法运算。
对于绝对值,我们有以下定义:
如果 $a > 0$,则 $|a| = a$
如果 $a = 0$,则 $|a| = 0$
如果 $a < 0$,则 $|a| = -a$
根据这些定义,我们可以计算出每个绝对值的值,然后进行有理数的乘除法运算。
【答案】:
(1)
解:
首先,我们计算两个数的绝对值:
$\left|-\frac{2}{3}\right| = \frac{2}{3}$
$\left|+\frac{14}{3}\right| = \frac{14}{3}$
然后,我们进行除法运算:
$\frac{2}{3} ÷ \frac{14}{3} = \frac{2}{3} × \frac{3}{14} = \frac{1}{7}$
(2)
解:
首先,我们计算各个数的绝对值:
$|-3| = 3$
$|-6| = 6$
$|-7| = 7$
$|+2| = 2$
然后,我们进行乘法和减法运算:
$3 × 6 - 7 × 2 = 18 - 14 = 4$
9. 如果$|x|= 2$,那么x的值为(
A.2
B.-2
C.2或-2
D.2或$-\frac{1}{2}$
C
)A.2
B.-2
C.2或-2
D.2或$-\frac{1}{2}$
答案:【解析】:
本题考查绝对值的定义。绝对值表示一个数到0的距离,因此,对于任何正数a,有$|a|=a$;对于任何负数b,有$|b|=-b$。所以,当$|x|=2$时,x可以是2或-2,因为这两个数到0的距离都是2。
【答案】:
C. $2$或$-2$
本题考查绝对值的定义。绝对值表示一个数到0的距离,因此,对于任何正数a,有$|a|=a$;对于任何负数b,有$|b|=-b$。所以,当$|x|=2$时,x可以是2或-2,因为这两个数到0的距离都是2。
【答案】:
C. $2$或$-2$
10. 已知有理数x在数轴上的位置如图所示,则下列结论正确的是(
A.$|x|<1$
B.$|x|<0$
C.$1<|x|<2$
D.$|x|>2$
D
)A.$|x|<1$
B.$|x|<0$
C.$1<|x|<2$
D.$|x|>2$
答案:解:由数轴可知,x位于-2左侧,即x<-2,
则|x|=-x>2,
故选D。
则|x|=-x>2,
故选D。
11. 亮点原创 对于有理数m,n,p,q,给出如下定义:如果$|m-p|+|n-p|= q$,那么称m和n关于p的“最佳间距”为q.根据上述定义,若a和6关于2的“最佳间距”为10,则a的值为(
A.6
B.8
C.8或-6
D.8或-4
D
)A.6
B.8
C.8或-6
D.8或-4
答案:【解析】:
本题主要考察绝对值的性质和定义方程的应用。
根据题目中“最佳间距”的定义,需要解绝对值方程$|a-2|+|6-2|=10$,
即$|a-2|+4=10$,
移项得$|a-2|=6$,
根据绝对值的定义,如果$|x|=k$,那么$x=k$或$x=-k$,
所以,可以得到两个方程:
$a-2=6$ 或 $a-2=-6$,
解第一个方程得 $a=8$,
解第二个方程得 $a=-4$,
所以,$a$的值为8或-4。
【答案】:
D
本题主要考察绝对值的性质和定义方程的应用。
根据题目中“最佳间距”的定义,需要解绝对值方程$|a-2|+|6-2|=10$,
即$|a-2|+4=10$,
移项得$|a-2|=6$,
根据绝对值的定义,如果$|x|=k$,那么$x=k$或$x=-k$,
所以,可以得到两个方程:
$a-2=6$ 或 $a-2=-6$,
解第一个方程得 $a=8$,
解第二个方程得 $a=-4$,
所以,$a$的值为8或-4。
【答案】:
D
12. 若有理数a在数轴上的对应点在原点的左边,且$|a|= 9$,则$a= $
-9
.答案:【解析】:
本题考查绝对值的定义和性质。
绝对值表示一个数到原点的距离,因此,若一个数的绝对值为9,则这个数可以是9或-9。
但题目中明确给出有理数a在数轴上的对应点在原点的左边,即a是负数。
所以,结合绝对值的性质和题目条件,可以确定$a = -9$。
【答案】:
$a = -9$
本题考查绝对值的定义和性质。
绝对值表示一个数到原点的距离,因此,若一个数的绝对值为9,则这个数可以是9或-9。
但题目中明确给出有理数a在数轴上的对应点在原点的左边,即a是负数。
所以,结合绝对值的性质和题目条件,可以确定$a = -9$。
【答案】:
$a = -9$
13. 若$|-x|= 2$,则$x= $
$\pm 2$
;若$|x-2|= 0$,则$x= $$2$
.答案:【解析】:
本题主要考察绝对值的定义和性质。
对于$|-x|= 2$,由绝对值的定义,我们知道绝对值表示一个数到0的距离,因此$|-x|= 2$可以拆分为两个方程:$-x = 2$ 或 $-x = -2$。
解这两个方程,我们得到$x = -2$ 或 $x = 2$。
对于$|x-2|= 0$,由绝对值的性质,一个数的绝对值等于0当且仅当这个数等于0。
所以我们有$x-2 = 0$,解这个方程我们得到$x = 2$。
【答案】:
$x = \pm 2$;$x = 2$。
本题主要考察绝对值的定义和性质。
对于$|-x|= 2$,由绝对值的定义,我们知道绝对值表示一个数到0的距离,因此$|-x|= 2$可以拆分为两个方程:$-x = 2$ 或 $-x = -2$。
解这两个方程,我们得到$x = -2$ 或 $x = 2$。
对于$|x-2|= 0$,由绝对值的性质,一个数的绝对值等于0当且仅当这个数等于0。
所以我们有$x-2 = 0$,解这个方程我们得到$x = 2$。
【答案】:
$x = \pm 2$;$x = 2$。