14. (2025·江苏苏州期末)若数轴上A,B两点表示的数互为相反数,点A在原点的左侧,并且A,B两点之间的距离是8,则点B表示的数是
4
.答案:【解析】:
本题考查了相反数的概念以及数轴上两点间的距离。
相反数的定义是:如果两个数的和等于零,那么这两个数互为相反数。
设点A表示的数为$a$,由于A、B两点表示的数互为相反数,所以点B表示的数为$-a$。
根据题意,A在原点的左侧,所以$a < 0$。
又因为A、B两点之间的距离是8,所以有:
$|-a - a| = 8$,
$|-2a| = 8$,
由于$a < 0$,所以$-2a > 0$,直接去掉绝对值符号得:
$-2a = 8$,
$a = -4$,
所以,点B表示的数为$-(-4) = 4$。
【答案】:
4。
本题考查了相反数的概念以及数轴上两点间的距离。
相反数的定义是:如果两个数的和等于零,那么这两个数互为相反数。
设点A表示的数为$a$,由于A、B两点表示的数互为相反数,所以点B表示的数为$-a$。
根据题意,A在原点的左侧,所以$a < 0$。
又因为A、B两点之间的距离是8,所以有:
$|-a - a| = 8$,
$|-2a| = 8$,
由于$a < 0$,所以$-2a > 0$,直接去掉绝对值符号得:
$-2a = 8$,
$a = -4$,
所以,点B表示的数为$-(-4) = 4$。
【答案】:
4。
15. 小花在做题时画了一条数轴,数轴上原有一点A,其表示的数是-2,由于粗心,小花把数轴的原点标错了位置,使得点A正好落在-2的相反数的位置,则要想把数轴画正确,原点应怎样移动?
答案:解:-2的相反数是2。
点A原表示-2,现落在2的位置,说明原点向右移动了$2 - (-2) = 4$个单位长度。
要画正确数轴,原点应向左移动4个单位长度。
答:原点应向左移动4个单位长度。
点A原表示-2,现落在2的位置,说明原点向右移动了$2 - (-2) = 4$个单位长度。
要画正确数轴,原点应向左移动4个单位长度。
答:原点应向左移动4个单位长度。
16. 如图,数轴的单位长度为1,点A,B,C,D,E在数轴上.请解答下列问题:
(1) 如果点A,C表示的数互为相反数,那么点D表示的数是多少?
(2) 如果点B,E表示的数互为相反数,那么点A表示的数的相反数是多少?
(3) 如果C是原点,现数轴上有一点P,距离点A表示的数的相反数对应的点5个单位长度,那么点P表示的数是多少?
(4) 在数轴上,点P表示的数是a,将点P平移100个单位长度后,点P表示的数和a互为相反数,求a的值.
]
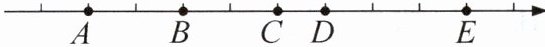
(1) 如果点A,C表示的数互为相反数,那么点D表示的数是多少?
(2) 如果点B,E表示的数互为相反数,那么点A表示的数的相反数是多少?
(3) 如果C是原点,现数轴上有一点P,距离点A表示的数的相反数对应的点5个单位长度,那么点P表示的数是多少?
(4) 在数轴上,点P表示的数是a,将点P平移100个单位长度后,点P表示的数和a互为相反数,求a的值.
]
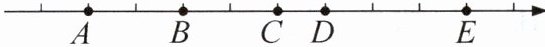
答案:(1) 解:因为点A、C表示的数互为相反数,且A、C之间有4个单位长度,所以点A表示-2,点C表示2。则点D在点C右侧1个单位,点D表示的数是3。
(2) 解:因为点B、E表示的数互为相反数,且B、E之间有8个单位长度,所以点B表示-4,点E表示4。点A在点B左侧2个单位,点A表示-6,其相反数是6。
(3) 解:若C是原点,点A在点C左侧3个单位,点A表示-3,其相反数对应的点表示3。距离3五个单位长度的点P表示的数是3+5=8或3-5=-2。
(4) 解:当点P向右平移100个单位时,a+100=-a,解得a=-50;当点P向左平移100个单位时,a-100=-a,解得a=50。所以a的值为50或-50。
(2) 解:因为点B、E表示的数互为相反数,且B、E之间有8个单位长度,所以点B表示-4,点E表示4。点A在点B左侧2个单位,点A表示-6,其相反数是6。
(3) 解:若C是原点,点A在点C左侧3个单位,点A表示-3,其相反数对应的点表示3。距离3五个单位长度的点P表示的数是3+5=8或3-5=-2。
(4) 解:当点P向右平移100个单位时,a+100=-a,解得a=-50;当点P向左平移100个单位时,a-100=-a,解得a=50。所以a的值为50或-50。
17. 已知数轴上A,B两点之间的距离为12,且A,B两点表示的数互为相反数.点A沿着数轴先向右运动2s,再向左运动5s到达点C的位置.若点A的运动速度始终为每秒1.5个单位长度,则点C表示的数的相反数为 (
A.-1.5或10.5
B.1.5或-10.5
C.1.5或10.5
D.-1.5或-10.5
A
)A.-1.5或10.5
B.1.5或-10.5
C.1.5或10.5
D.-1.5或-10.5
答案:解:设点A表示的数为a,则点B表示的数为-a。
∵A,B两点之间的距离为12,
∴|a - (-a)| = 12,即|2a| = 12,解得a = 6或a = -6。
情况一:当a = 6时,
点A运动的路程:先向右运动2s,路程为2×1.5 = 3;再向左运动5s,路程为5×1.5 = 7.5。
点A最终位置:6 + 3 - 7.5 = 1.5,即点C表示的数为1.5。
点C表示的数的相反数为-1.5。
情况二:当a = -6时,
点A运动的路程:先向右运动2s,路程为2×1.5 = 3;再向左运动5s,路程为5×1.5 = 7.5。
点A最终位置:-6 + 3 - 7.5 = -10.5,即点C表示的数为-10.5。
点C表示的数的相反数为10.5。
综上,点C表示的数的相反数为-1.5或10.5。
答案:A
∵A,B两点之间的距离为12,
∴|a - (-a)| = 12,即|2a| = 12,解得a = 6或a = -6。
情况一:当a = 6时,
点A运动的路程:先向右运动2s,路程为2×1.5 = 3;再向左运动5s,路程为5×1.5 = 7.5。
点A最终位置:6 + 3 - 7.5 = 1.5,即点C表示的数为1.5。
点C表示的数的相反数为-1.5。
情况二:当a = -6时,
点A运动的路程:先向右运动2s,路程为2×1.5 = 3;再向左运动5s,路程为5×1.5 = 7.5。
点A最终位置:-6 + 3 - 7.5 = -10.5,即点C表示的数为-10.5。
点C表示的数的相反数为10.5。
综上,点C表示的数的相反数为-1.5或10.5。
答案:A
18. (2025·江苏泰州期末)已知数轴上点A表示的数为-3,B,C两点表示的数互为相反数,且点B到点A的距离为2,则点C表示的数为____
5或1
.答案:【解析】:
本题主要考查了数轴上两点间的距离公式和相反数的性质。
首先,根据题目条件,点A表示的数为-3,点B到点A的距离为2。
在数轴上,两点间的距离等于它们所表示数的差的绝对值。
设点B表示的数为$x$,
则有$|x - (-3)| = 2$,
即$|x + 3| = 2$。
解这个绝对值方程,我们得到两个$x + 3 = 2$ 或 $x + 3 = -2$,
解得$x = -1$ 或 $x = -5$。
由于B,C两点表示的数互为相反数,根据相反数的定义,如果点B表示的数为$x$,那么点C表示的数为$-x$。
所以,当点B表示的数为-1时,点C表示的数为1;
当点B表示的数为-5时,点C表示的数为5。
【答案】:
5或1
本题主要考查了数轴上两点间的距离公式和相反数的性质。
首先,根据题目条件,点A表示的数为-3,点B到点A的距离为2。
在数轴上,两点间的距离等于它们所表示数的差的绝对值。
设点B表示的数为$x$,
则有$|x - (-3)| = 2$,
即$|x + 3| = 2$。
解这个绝对值方程,我们得到两个$x + 3 = 2$ 或 $x + 3 = -2$,
解得$x = -1$ 或 $x = -5$。
由于B,C两点表示的数互为相反数,根据相反数的定义,如果点B表示的数为$x$,那么点C表示的数为$-x$。
所以,当点B表示的数为-1时,点C表示的数为1;
当点B表示的数为-5时,点C表示的数为5。
【答案】:
5或1
19. 新趋势 推导探究 化简下列各式,并解答问题:
$-(-2);+(-\frac{1}{5});-[ -(-4)];$
$-[ -(+3.5)];-\{ -[ -(-5)]\} ;$
$-\{ -[ -(+5)]\} .$
(1) 当+5前面有2025个负号时,化简后的结果是多少?
(2) 当-5前面有2024个负号时,化简后的结果是多少?
(3) 根据以上解答,你能总结出什么规律?
$-(-2);+(-\frac{1}{5});-[ -(-4)];$
$-[ -(+3.5)];-\{ -[ -(-5)]\} ;$
$-\{ -[ -(+5)]\} .$
(1) 当+5前面有2025个负号时,化简后的结果是多少?
(2) 当-5前面有2024个负号时,化简后的结果是多少?
(3) 根据以上解答,你能总结出什么规律?
答案:【解析】:
本题主要考察相反数的定义和性质,以及如何根据负号的数量判断数的化简结果。
相反数的定义是:一个数与它的相反数相加等于零。例如,5和-5是相反数。
对于形如“-(-a)”的表达式,根据相反数的性质,它等于a。即,负负得正。
对于形如“-[-(a)]”或更复杂的嵌套形式,我们可以逐步去掉内层的负号,根据相反数的性质进行化简。
当+5前面有2025个负号时,由于负负得正,但负号的总数是奇数,所以最后的结果是负的。即,$-(+5) = -5$,但因为有2025个负号,所以结果是$-5$(因为奇数个负号相当于一个负号)。但考虑到初始的+5前的正号,实际上就是$-5$前面有2024个负号再加上一个负号,即结果为$-5$的相反数的相反数...(经过2024次取反后回到原数),再取反得$-5$。但直接理解就是奇数个负号等于原数取反,所以答案是$-5$。但更简洁的理解是:奇数个负号作用于一个正数,结果为该数的相反数。
当-5前面有2024个负号时,由于负负得正,且负号的总数是偶数,所以最后的结果是正的。即,$-(-5) = 5$,因为有2024个负号(偶数个),所以结果仍然是5。
根据以上解答,可以总结出规律:当一个数前面有偶数个负号时,化简后的结果等于该数本身;当一个数前面有奇数个负号时,化简后的结果等于该数的相反数。
【答案】:
(1) 当+5前面有2025个负号时,化简后的结果是$-5$。
(2) 当-5前面有2024个负号时,化简后的结果是$5$。
(3) 规律:当一个数前面有偶数个负号时,化简后的结果等于该数本身;当一个数前面有奇数个负号时,化简后的结果等于该数的相反数。
本题主要考察相反数的定义和性质,以及如何根据负号的数量判断数的化简结果。
相反数的定义是:一个数与它的相反数相加等于零。例如,5和-5是相反数。
对于形如“-(-a)”的表达式,根据相反数的性质,它等于a。即,负负得正。
对于形如“-[-(a)]”或更复杂的嵌套形式,我们可以逐步去掉内层的负号,根据相反数的性质进行化简。
当+5前面有2025个负号时,由于负负得正,但负号的总数是奇数,所以最后的结果是负的。即,$-(+5) = -5$,但因为有2025个负号,所以结果是$-5$(因为奇数个负号相当于一个负号)。但考虑到初始的+5前的正号,实际上就是$-5$前面有2024个负号再加上一个负号,即结果为$-5$的相反数的相反数...(经过2024次取反后回到原数),再取反得$-5$。但直接理解就是奇数个负号等于原数取反,所以答案是$-5$。但更简洁的理解是:奇数个负号作用于一个正数,结果为该数的相反数。
当-5前面有2024个负号时,由于负负得正,且负号的总数是偶数,所以最后的结果是正的。即,$-(-5) = 5$,因为有2024个负号(偶数个),所以结果仍然是5。
根据以上解答,可以总结出规律:当一个数前面有偶数个负号时,化简后的结果等于该数本身;当一个数前面有奇数个负号时,化简后的结果等于该数的相反数。
【答案】:
(1) 当+5前面有2025个负号时,化简后的结果是$-5$。
(2) 当-5前面有2024个负号时,化简后的结果是$5$。
(3) 规律:当一个数前面有偶数个负号时,化简后的结果等于该数本身;当一个数前面有奇数个负号时,化简后的结果等于该数的相反数。