1. 给出下列各数:$-4$,$-2.8$,0,$|-4|$.其中比$-3$小的数是(
A.$-4$
B.$|-4|$
C.0
D.$-2.8$
A
)A.$-4$
B.$|-4|$
C.0
D.$-2.8$
答案:【解析】:
本题主要考查了数的大小比较和绝对值的定义。题目给出了四个数:$-4$,$-2.8$,$0$,$|-4|$,要求我们找出其中小于$-3$的数。
首先,我们可以逐一比较这些数与$-3$的大小。
对于$-4$,显然有$-4 < -3$。
对于$-2.8$,由于$-2.8 > -3$,所以$-2.8$不满足条件。
对于$0$,显然$0 > -3$,所以$0$也不满足条件。
对于$|-4|$,根据绝对值的定义,$|-4| = 4$,显然$4 > -3$,所以$|-4|$也不满足条件。
综上,只有$-4$是小于$-3$的数。
【答案】:
A
本题主要考查了数的大小比较和绝对值的定义。题目给出了四个数:$-4$,$-2.8$,$0$,$|-4|$,要求我们找出其中小于$-3$的数。
首先,我们可以逐一比较这些数与$-3$的大小。
对于$-4$,显然有$-4 < -3$。
对于$-2.8$,由于$-2.8 > -3$,所以$-2.8$不满足条件。
对于$0$,显然$0 > -3$,所以$0$也不满足条件。
对于$|-4|$,根据绝对值的定义,$|-4| = 4$,显然$4 > -3$,所以$|-4|$也不满足条件。
综上,只有$-4$是小于$-3$的数。
【答案】:
A
2. $-3$的绝对值的相反数是(
A.3
B.$-\frac{1}{3}$
C.$-3$
D.$\frac{1}{3}$
C
)A.3
B.$-\frac{1}{3}$
C.$-3$
D.$\frac{1}{3}$
答案:【解析】:
本题主要考察绝对值的定义和性质以及相反数的概念。
首先,根据绝对值的定义,对于任意实数$x$,其绝对值$|x|$满足:
$|x| =\begin{cases}x, x \geq 0 \\ -x, x < 0\end{cases}$
所以,$|-3|$的值为3。
再根据相反数的定义,一个数与其相反数的和为0。
因此,3的相反数是-3。
所以,$|-3|$的相反数是-3。
【答案】:
C. $-3$
本题主要考察绝对值的定义和性质以及相反数的概念。
首先,根据绝对值的定义,对于任意实数$x$,其绝对值$|x|$满足:
$|x| =\begin{cases}x, x \geq 0 \\ -x, x < 0\end{cases}$
所以,$|-3|$的值为3。
再根据相反数的定义,一个数与其相反数的和为0。
因此,3的相反数是-3。
所以,$|-3|$的相反数是-3。
【答案】:
C. $-3$
3. 有理数$-\frac{1}{5}$,$-\frac{2}{5}和-\frac{3}{5}$之间的大小关系是(
A.$-\frac{1}{5}<-\frac{2}{5}<-\frac{3}{5}$
B.$-\frac{3}{5}<-\frac{2}{5}<-\frac{1}{5}$
C.$-\frac{3}{5}<-\frac{1}{5}<-\frac{2}{5}$
D.$-\frac{1}{5}<-\frac{3}{5}<-\frac{2}{5}$
B
)A.$-\frac{1}{5}<-\frac{2}{5}<-\frac{3}{5}$
B.$-\frac{3}{5}<-\frac{2}{5}<-\frac{1}{5}$
C.$-\frac{3}{5}<-\frac{1}{5}<-\frac{2}{5}$
D.$-\frac{1}{5}<-\frac{3}{5}<-\frac{2}{5}$
答案:【解析】:
本题考查有理数的大小比较,特别是负数之间的大小关系。
对于负数,绝对值越大的数实际上越小。
因此,我们可以通过比较这些数的绝对值来确定它们之间的大小关系。
首先,我们计算每个数的绝对值:
$|-\frac{1}{5}| = \frac{1}{5}$
$|-\frac{2}{5}| = \frac{2}{5}$
$|-\frac{3}{5}| = \frac{3}{5}$
由于 $\frac{3}{5} > \frac{2}{5} > \frac{1}{5}$,
根据负数的性质(绝对值越大的负数越小),
我们可以得出:
$-\frac{3}{5} < -\frac{2}{5} < -\frac{1}{5}$
【答案】:
B
本题考查有理数的大小比较,特别是负数之间的大小关系。
对于负数,绝对值越大的数实际上越小。
因此,我们可以通过比较这些数的绝对值来确定它们之间的大小关系。
首先,我们计算每个数的绝对值:
$|-\frac{1}{5}| = \frac{1}{5}$
$|-\frac{2}{5}| = \frac{2}{5}$
$|-\frac{3}{5}| = \frac{3}{5}$
由于 $\frac{3}{5} > \frac{2}{5} > \frac{1}{5}$,
根据负数的性质(绝对值越大的负数越小),
我们可以得出:
$-\frac{3}{5} < -\frac{2}{5} < -\frac{1}{5}$
【答案】:
B
4. 新趋势 开放探究 写出一个数,使这个数的绝对值等于它的相反数:
-1
.答案:【解析】:
本题考查绝对值的基本性质。
对于一个数$x$,若$x$为正数,则$|x| = x$;
若$x$为负数,则$|x| = -x$,即$x$的绝对值等于它的相反数;
若$x$为0,则$|0| = 0$,0的相反数也是0,满足条件。
因此,需要找的是一个负数或0。
以选择-1这个负数为例,其绝对值为$|-1| = 1$,而-1的相反数是1,满足条件。
当然,选择0也满足条件,因为$|0| = 0$,0的相反数也是0。
【答案】:
答案不唯一,如$-1$(或任何负数或0)。
本题考查绝对值的基本性质。
对于一个数$x$,若$x$为正数,则$|x| = x$;
若$x$为负数,则$|x| = -x$,即$x$的绝对值等于它的相反数;
若$x$为0,则$|0| = 0$,0的相反数也是0,满足条件。
因此,需要找的是一个负数或0。
以选择-1这个负数为例,其绝对值为$|-1| = 1$,而-1的相反数是1,满足条件。
当然,选择0也满足条件,因为$|0| = 0$,0的相反数也是0。
【答案】:
答案不唯一,如$-1$(或任何负数或0)。
5. (教材P28练习2变式)比较大小:(填“$>$”“$<$”或“$=$”)
(1)$|-5|$
(2)3
(3)$-|-\frac{2}{3}|$
(1)$|-5|$
>
$-5$;(2)3
<
$-(-4)$;(3)$-|-\frac{2}{3}|$
<
$-\frac{1}{2}$.答案:【解析】:
本题主要考查了绝对值的定义、性质以及利用绝对值比较两个数的大小。
对于第一组数,我们需要先计算绝对值,再根据绝对值的性质进行比较;
对于第二组数,我们需要先化简表达式,再进行比较;
对于第三组数,我们需要先分别求出两个数的绝对值,再比较它们的大小,并确定负数的绝对值大的反而小。
(1) 对于 $|-5|$ 和 $-5$:
根据绝对值的定义,$|-5| = 5$。
显然,正数5大于负数-5,所以 $|-5| > -5$。
(2) 对于 3 和 $-(-4)$:
根据负负得正的规则,$-(-4) = 4$。
显然,正数3小于正数4,所以 $3 < -(-4)$。
(3) 对于 $-|-\frac{2}{3}|$ 和 $-\frac{1}{2}$:
首先,根据绝对值的定义,$|-\frac{2}{3}| = \frac{2}{3}$。
再取负,得到 $-|-\frac{2}{3}| = -\frac{2}{3}$。
为了比较 $-\frac{2}{3}$ 和 $-\frac{1}{2}$ 的大小,我们可以先比较它们的绝对值 $\frac{2}{3}$ 和 $\frac{1}{2}$。
由于 $\frac{2}{3} > \frac{1}{2}$,根据负数比较大小的规则(绝对值大的负数反而小),所以 $-\frac{2}{3} < -\frac{1}{2}$。
即 $-|-\frac{2}{3}| < -\frac{1}{2}$。
【答案】:
(1) $>$
(2) $<$
(3) $<$
本题主要考查了绝对值的定义、性质以及利用绝对值比较两个数的大小。
对于第一组数,我们需要先计算绝对值,再根据绝对值的性质进行比较;
对于第二组数,我们需要先化简表达式,再进行比较;
对于第三组数,我们需要先分别求出两个数的绝对值,再比较它们的大小,并确定负数的绝对值大的反而小。
(1) 对于 $|-5|$ 和 $-5$:
根据绝对值的定义,$|-5| = 5$。
显然,正数5大于负数-5,所以 $|-5| > -5$。
(2) 对于 3 和 $-(-4)$:
根据负负得正的规则,$-(-4) = 4$。
显然,正数3小于正数4,所以 $3 < -(-4)$。
(3) 对于 $-|-\frac{2}{3}|$ 和 $-\frac{1}{2}$:
首先,根据绝对值的定义,$|-\frac{2}{3}| = \frac{2}{3}$。
再取负,得到 $-|-\frac{2}{3}| = -\frac{2}{3}$。
为了比较 $-\frac{2}{3}$ 和 $-\frac{1}{2}$ 的大小,我们可以先比较它们的绝对值 $\frac{2}{3}$ 和 $\frac{1}{2}$。
由于 $\frac{2}{3} > \frac{1}{2}$,根据负数比较大小的规则(绝对值大的负数反而小),所以 $-\frac{2}{3} < -\frac{1}{2}$。
即 $-|-\frac{2}{3}| < -\frac{1}{2}$。
【答案】:
(1) $>$
(2) $<$
(3) $<$
6. 若a,b在数轴上的位置如图所示,则a
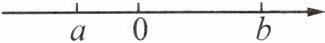
>
$-b$.(填“$>$”“$<$”或“$=$”)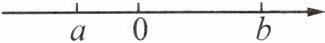
答案:解:由数轴可知,a<0,b>0,且|a|<|b|。
因为b>0,所以-b<0。
又因为|a|<|b|,所以|a|<|-b|。
两个负数比较大小,绝对值小的反而大,故a>-b。
>
因为b>0,所以-b<0。
又因为|a|<|b|,所以|a|<|-b|。
两个负数比较大小,绝对值小的反而大,故a>-b。
>
7. 在数轴上画出表示下列各数的点,并用“$<$”号将它们连接起来:$-(-3)$,$-|-2|$,0,$+(-1)$,$-(+3)$.


答案:【解析】:本题可先对所给的数进行化简,再在数轴上表示出这些数,最后根据数轴上数的大小比较规则将它们用“$<$”号连接起来。
步骤一:化简各数
$-(-3)$:根据“负负得正”的原则,$-(-3)=3$。
$-|-2|$:先求绝对值,$\vert -2\vert = 2$,再取其相反数,所以$-|-2|=-2$。
$+(-1)$:根据“正负得负”的原则,$+(-1)= -1$。
$-(+3)$:根据“正负得负”的原则,$-(+3)= -3$。
步骤二:在数轴上表示各数
在数轴上找到对应的点,分别表示出$3$,$-2$,$0$,$-1$,$-3$。
步骤三:比较各数大小并连接
根据数轴上数的大小比较规则:数轴上右边的数总比左边的数大。
从数轴上可以看出,这些数从左到右的顺序为$-3$,$-2$,$-1$,$0$,$3$,所以用“$<$”号连接起来为:$-(+3)<-|-2|<+(-1)<0<-(-3)$。
【答案】:$-(+3)<-|-2|<+(-1)<0<-(-3)$;图略。
步骤一:化简各数
$-(-3)$:根据“负负得正”的原则,$-(-3)=3$。
$-|-2|$:先求绝对值,$\vert -2\vert = 2$,再取其相反数,所以$-|-2|=-2$。
$+(-1)$:根据“正负得负”的原则,$+(-1)= -1$。
$-(+3)$:根据“正负得负”的原则,$-(+3)= -3$。
步骤二:在数轴上表示各数
在数轴上找到对应的点,分别表示出$3$,$-2$,$0$,$-1$,$-3$。
步骤三:比较各数大小并连接
根据数轴上数的大小比较规则:数轴上右边的数总比左边的数大。
从数轴上可以看出,这些数从左到右的顺序为$-3$,$-2$,$-1$,$0$,$3$,所以用“$<$”号连接起来为:$-(+3)<-|-2|<+(-1)<0<-(-3)$。
【答案】:$-(+3)<-|-2|<+(-1)<0<-(-3)$;图略。
8. (2025·江苏常州期末)已知$|a|= \frac{2}{3}$,$|b|= \frac{3}{5}$,求a,b的值,并比较它们的大小.
答案:【解析】:
本题主要考查了绝对值的定义以及利用绝对值比较数的大小。
首先,根据绝对值的定义,如果$|x| = k$,那么$x$可以是$k$或$-k$。
所以,对于给定的$|a| = \frac{2}{3}$,$a$可以是$\frac{2}{3}$或$-\frac{2}{3}$;
对于$|b| = \frac{3}{5}$,$b$可以是$\frac{3}{5}$或$-\frac{3}{5}$。
接下来,我们需要比较$a$和$b$的大小。
由于$a$和$b$各自有两个可能的值,我们需要分情况讨论:
当$a = \frac{2}{3}$,$b = \frac{3}{5}$时,为了比较它们的大小,我们可以将它们转换为相同的分母,
即$a = \frac{2}{3} = \frac{10}{15}$,$b = \frac{3}{5} = \frac{9}{15}$,
所以$a > b$;
当$a = \frac{2}{3}$,$b = -\frac{3}{5}$时,显然$a > b$;
当$a = -\frac{2}{3}$,$b = \frac{3}{5}$时,显然$a < b$;
当$a = -\frac{2}{3}$,$b = -\frac{3}{5}$时,同样为了比较它们的大小,我们可以将它们转换为相同的分母,
即$a = -\frac{2}{3} = -\frac{10}{15}$,$b = -\frac{3}{5} = -\frac{9}{15}$,
所以$a < b$。
【答案】:
$a$的值为$\pm \frac{2}{3}$,$b$的值为$\pm \frac{3}{5}$;
当$a = \frac{2}{3}$,$b = \frac{3}{5}$时,$a > b$;
当$a = \frac{2}{3}$,$b = -\frac{3}{5}$时,$a > b$;
当$a = -\frac{2}{3}$,$b = \frac{3}{5}$时,$a < b$;
当$a = -\frac{2}{3}$,$b = -\frac{3}{5}$时,$a < b$。
本题主要考查了绝对值的定义以及利用绝对值比较数的大小。
首先,根据绝对值的定义,如果$|x| = k$,那么$x$可以是$k$或$-k$。
所以,对于给定的$|a| = \frac{2}{3}$,$a$可以是$\frac{2}{3}$或$-\frac{2}{3}$;
对于$|b| = \frac{3}{5}$,$b$可以是$\frac{3}{5}$或$-\frac{3}{5}$。
接下来,我们需要比较$a$和$b$的大小。
由于$a$和$b$各自有两个可能的值,我们需要分情况讨论:
当$a = \frac{2}{3}$,$b = \frac{3}{5}$时,为了比较它们的大小,我们可以将它们转换为相同的分母,
即$a = \frac{2}{3} = \frac{10}{15}$,$b = \frac{3}{5} = \frac{9}{15}$,
所以$a > b$;
当$a = \frac{2}{3}$,$b = -\frac{3}{5}$时,显然$a > b$;
当$a = -\frac{2}{3}$,$b = \frac{3}{5}$时,显然$a < b$;
当$a = -\frac{2}{3}$,$b = -\frac{3}{5}$时,同样为了比较它们的大小,我们可以将它们转换为相同的分母,
即$a = -\frac{2}{3} = -\frac{10}{15}$,$b = -\frac{3}{5} = -\frac{9}{15}$,
所以$a < b$。
【答案】:
$a$的值为$\pm \frac{2}{3}$,$b$的值为$\pm \frac{3}{5}$;
当$a = \frac{2}{3}$,$b = \frac{3}{5}$时,$a > b$;
当$a = \frac{2}{3}$,$b = -\frac{3}{5}$时,$a > b$;
当$a = -\frac{2}{3}$,$b = \frac{3}{5}$时,$a < b$;
当$a = -\frac{2}{3}$,$b = -\frac{3}{5}$时,$a < b$。
9. 下列比较大小正确的是(
A.$-(-21)<+(-21)$
B.$-|-10\frac{1}{2}|>8\frac{2}{3}$
C.$-|-7\frac{2}{3}|= -(-7\frac{2}{3})$
D.$-\frac{5}{6}<-\frac{4}{5}$
D
)A.$-(-21)<+(-21)$
B.$-|-10\frac{1}{2}|>8\frac{2}{3}$
C.$-|-7\frac{2}{3}|= -(-7\frac{2}{3})$
D.$-\frac{5}{6}<-\frac{4}{5}$
答案:【解析】:
本题主要考察绝对值的定义和性质,以及数的大小比较。
A. 对于选项A,有 $-(-21) = 21$,而 $+(-21) = -21$,显然 $21 > -21$,所以A选项错误。
B. 对于选项B,有 $-|-10\frac{1}{2}| = -10\frac{1}{2}$,显然 $-10\frac{1}{2} < 8\frac{2}{3}$,所以B选项错误。
C. 对于选项C,有 $-|-7\frac{2}{3}| = -7\frac{2}{3}$,而 $-(-7\frac{2}{3}) = 7\frac{2}{3}$,显然 $-7\frac{2}{3} \neq 7\frac{2}{3}$,所以C选项错误。
D. 对于选项D,首先求两数的绝对值,有 $|-\frac{5}{6}| = \frac{5}{6}$,$|-\frac{4}{5}| = \frac{4}{5}$。
为了比较这两个分数,我们可以将它们转换为相同的分母,即 $\frac{5}{6} = \frac{25}{30}$,$\frac{4}{5} = \frac{24}{30}$。
显然,$\frac{25}{30} > \frac{24}{30}$,所以 $-\frac{5}{6} < -\frac{4}{5}$,D选项正确。
【答案】:
D
本题主要考察绝对值的定义和性质,以及数的大小比较。
A. 对于选项A,有 $-(-21) = 21$,而 $+(-21) = -21$,显然 $21 > -21$,所以A选项错误。
B. 对于选项B,有 $-|-10\frac{1}{2}| = -10\frac{1}{2}$,显然 $-10\frac{1}{2} < 8\frac{2}{3}$,所以B选项错误。
C. 对于选项C,有 $-|-7\frac{2}{3}| = -7\frac{2}{3}$,而 $-(-7\frac{2}{3}) = 7\frac{2}{3}$,显然 $-7\frac{2}{3} \neq 7\frac{2}{3}$,所以C选项错误。
D. 对于选项D,首先求两数的绝对值,有 $|-\frac{5}{6}| = \frac{5}{6}$,$|-\frac{4}{5}| = \frac{4}{5}$。
为了比较这两个分数,我们可以将它们转换为相同的分母,即 $\frac{5}{6} = \frac{25}{30}$,$\frac{4}{5} = \frac{24}{30}$。
显然,$\frac{25}{30} > \frac{24}{30}$,所以 $-\frac{5}{6} < -\frac{4}{5}$,D选项正确。
【答案】:
D
10. 下列各式正确的是(
A.$-|-5|= 5$
B.$-(-5)= -5$
C.$|-5|= -5$
D.$-(-5)= 5$
D
)A.$-|-5|= 5$
B.$-(-5)= -5$
C.$|-5|= -5$
D.$-(-5)= 5$
答案:【解析】:
本题主要考察绝对值的定义及性质,以及负负得正的规则。
A选项:计算$-|-5|$,根据绝对值的定义,$|-5|=5$,所以$-|-5|=-5$,与选项A给出的$5$不符,故A错误。
B选项:计算$-(-5)$,根据负负得正的规则,$-(-5)=5$,与选项B给出的$-5$不符,故B错误。
C选项:计算$|-5|$,根据绝对值的定义,$|-5|=5$,与选项C给出的$-5$不符,故C错误。
D选项:计算$-(-5)$,根据负负得正的规则,$-(-5)=5$,与选项D给出的$5$相符,故D正确。
【答案】:
D
本题主要考察绝对值的定义及性质,以及负负得正的规则。
A选项:计算$-|-5|$,根据绝对值的定义,$|-5|=5$,所以$-|-5|=-5$,与选项A给出的$5$不符,故A错误。
B选项:计算$-(-5)$,根据负负得正的规则,$-(-5)=5$,与选项B给出的$-5$不符,故B错误。
C选项:计算$|-5|$,根据绝对值的定义,$|-5|=5$,与选项C给出的$-5$不符,故C错误。
D选项:计算$-(-5)$,根据负负得正的规则,$-(-5)=5$,与选项D给出的$5$相符,故D正确。
【答案】:
D