11. 如果甲数的绝对值大于乙数的绝对值,那么下列说法正确的是(
A.甲数必定大于乙数
B.甲数必定小于乙数
C.甲、乙两数一定异号
D.甲数对应的点与原点的距离大于乙数对应的点与原点的距离
D
)A.甲数必定大于乙数
B.甲数必定小于乙数
C.甲、乙两数一定异号
D.甲数对应的点与原点的距离大于乙数对应的点与原点的距离
答案:【解析】:
本题主要考察绝对值的定义及性质。
绝对值表示一个数对应的点与原点的距离。
分析选项:
A. 甲数必定大于乙数:这是不正确的,因为绝对值大并不意味着原数一定大,例如甲数为-5,乙数为3,虽然$|-5| > |3|$,但-5<3,所以A选项错误。
B. 甲数必定小于乙数:这同样是不正确的,原因同上,例如甲数为5,乙数为-3,虽然$|5| > |-3|$,但5>-3,所以B选项错误。
C. 甲、乙两数一定异号:这也是不正确的,因为绝对值的大小与数的符号无关,例如甲数为5,乙数为3,虽然$|5| > |3|$,但两者都是正数,所以C选项错误。
D. 甲数对应的点与原点的距离大于乙数对应的点与原点的距离:这是正确的,因为绝对值就是表示一个数对应的点与原点的距离。
综上所述,只有D选项是正确的。
【答案】:
D
本题主要考察绝对值的定义及性质。
绝对值表示一个数对应的点与原点的距离。
分析选项:
A. 甲数必定大于乙数:这是不正确的,因为绝对值大并不意味着原数一定大,例如甲数为-5,乙数为3,虽然$|-5| > |3|$,但-5<3,所以A选项错误。
B. 甲数必定小于乙数:这同样是不正确的,原因同上,例如甲数为5,乙数为-3,虽然$|5| > |-3|$,但5>-3,所以B选项错误。
C. 甲、乙两数一定异号:这也是不正确的,因为绝对值的大小与数的符号无关,例如甲数为5,乙数为3,虽然$|5| > |3|$,但两者都是正数,所以C选项错误。
D. 甲数对应的点与原点的距离大于乙数对应的点与原点的距离:这是正确的,因为绝对值就是表示一个数对应的点与原点的距离。
综上所述,只有D选项是正确的。
【答案】:
D
12. (2024·江苏南京)比较大小:$-\frac{2}{3}$
<
$-\frac{4}{9}$.(填“$>$”“$<$”或“$=$”)答案:【解析】:
本题考查的是通过绝对值比较两个负数的大小。根据有理数比较大小的法则:两个负数比较大小,绝对值大的反而小。我们需要先求出两个数的绝对值,然后比较它们的大小,最后根据法则确定原数的大小关系。
首先,我们计算两个数的绝对值:
$|-\frac{2}{3}| = \frac{2}{3} = \frac{2 × 3}{3 × 3} = \frac{6}{9}$
$|-\frac{4}{9}| = \frac{4}{9}$
接着,我们比较两个绝对值的大小:
$\frac{6}{9} > \frac{4}{9}$
由于两个数都是负数,且$-\frac{2}{3}$的绝对值大于$-\frac{4}{9}$的绝对值,根据有理数比较大小的法则,我们可以得出:
$-\frac{2}{3} < -\frac{4}{9}$
【答案】:
$<$
本题考查的是通过绝对值比较两个负数的大小。根据有理数比较大小的法则:两个负数比较大小,绝对值大的反而小。我们需要先求出两个数的绝对值,然后比较它们的大小,最后根据法则确定原数的大小关系。
首先,我们计算两个数的绝对值:
$|-\frac{2}{3}| = \frac{2}{3} = \frac{2 × 3}{3 × 3} = \frac{6}{9}$
$|-\frac{4}{9}| = \frac{4}{9}$
接着,我们比较两个绝对值的大小:
$\frac{6}{9} > \frac{4}{9}$
由于两个数都是负数,且$-\frac{2}{3}$的绝对值大于$-\frac{4}{9}$的绝对值,根据有理数比较大小的法则,我们可以得出:
$-\frac{2}{3} < -\frac{4}{9}$
【答案】:
$<$
13. 若$a= -4$,且$|-a|= |b|$,则$b= $
$\pm 4$
.答案:【解析】:
本题主要考查绝对值的定义和性质。绝对值表示一个数到0的距离,因此,对于任何实数x,其绝对值|x|都是非负的。给定$a = -4$,我们可以先求出|-a|的值,再根据|--a| = |b|来求解b的值。
首先,根据绝对值的定义,我们有
$|-a| = |-(-4)| = 4$,
由题目条件,我们知道|b| = |--a|,所以
$|b| = 4$,
根据绝对值的性质,我们可以得出b的两个可能值:
$b = 4 \text{ 或 } b = -4$。
【答案】:
$b = \pm 4$。
本题主要考查绝对值的定义和性质。绝对值表示一个数到0的距离,因此,对于任何实数x,其绝对值|x|都是非负的。给定$a = -4$,我们可以先求出|-a|的值,再根据|--a| = |b|来求解b的值。
首先,根据绝对值的定义,我们有
$|-a| = |-(-4)| = 4$,
由题目条件,我们知道|b| = |--a|,所以
$|b| = 4$,
根据绝对值的性质,我们可以得出b的两个可能值:
$b = 4 \text{ 或 } b = -4$。
【答案】:
$b = \pm 4$。
14. 若$|m|= m$,则m为
非负
数;若$|m|= -m$,则m为非正
数.答案:【解析】:
本题主要考察绝对值的定义和性质。
对于$|m| = m$,由绝对值的定义可知,当$m \geq 0$时,$|m| = m$。
对于$|m| = -m$,由绝对值的定义可知,当$m \leq 0$时,$|m| = -m$。
【答案】:
非负;非正。
本题主要考察绝对值的定义和性质。
对于$|m| = m$,由绝对值的定义可知,当$m \geq 0$时,$|m| = m$。
对于$|m| = -m$,由绝对值的定义可知,当$m \leq 0$时,$|m| = -m$。
【答案】:
非负;非正。
15. 已知$a>0$,$b<0$,且$|a|>|b|$,试比较a,$-a$,b,$-b$的大小.
答案:【解析】:
本题主要考察绝对值的性质以及数的大小比较。
首先,根据题目条件,知道$a>0$,$b<0$,且$|a|>|b|$。
这意味着$a$是正数,$b$是负数,且$a$的绝对值大于$b$的绝对值。
接下来,可以根据绝对值的定义,得出$-a$和$-b$的符号以及它们与$a$和$b$的关系。
由于$a>0$,所以$-a<0$;
由于$b<0$,所以$-b>0$。
又因为$|a|>|b|$,所以$-a$的绝对值(即$-(-a)=a$)大于$b$的绝对值(即$-b$的相反数),而$a$的绝对值(即它本身)大于$-b$(因为$-b$是正数且小于$a$的绝对值)。
同时,$b$作为负数,其值必然小于任何正数和0,也小于其相反数$-b$。
综合以上信息,可以得出:
$a$是正数且绝对值最大,所以$a$最大;
$-b$是正数但绝对值小于$a$,所以$-b$次之;
$b$是负数,所以$b$小于$a$和$-b$;
$-a$是负数且绝对值大于$b$但小于$a$的绝对值,所以$-a$最小(在负数中,绝对值大的数实际上更小)。
所以,最终的大小关系是:$-a<b<-b<a$。
【答案】:
$-a<b<-b<a$。
本题主要考察绝对值的性质以及数的大小比较。
首先,根据题目条件,知道$a>0$,$b<0$,且$|a|>|b|$。
这意味着$a$是正数,$b$是负数,且$a$的绝对值大于$b$的绝对值。
接下来,可以根据绝对值的定义,得出$-a$和$-b$的符号以及它们与$a$和$b$的关系。
由于$a>0$,所以$-a<0$;
由于$b<0$,所以$-b>0$。
又因为$|a|>|b|$,所以$-a$的绝对值(即$-(-a)=a$)大于$b$的绝对值(即$-b$的相反数),而$a$的绝对值(即它本身)大于$-b$(因为$-b$是正数且小于$a$的绝对值)。
同时,$b$作为负数,其值必然小于任何正数和0,也小于其相反数$-b$。
综合以上信息,可以得出:
$a$是正数且绝对值最大,所以$a$最大;
$-b$是正数但绝对值小于$a$,所以$-b$次之;
$b$是负数,所以$b$小于$a$和$-b$;
$-a$是负数且绝对值大于$b$但小于$a$的绝对值,所以$-a$最小(在负数中,绝对值大的数实际上更小)。
所以,最终的大小关系是:$-a<b<-b<a$。
【答案】:
$-a<b<-b<a$。
16. 已知有理数a,b,c,d中,a,d为负数,b,c为正数,且$|c|>|b|>|d|>|a|$.
(1)画出数轴,并标出表示数a,b,c,d的点的大致位置;
(2)将a,c,d,$-a$,$-c$,$-d$按照从小到大的顺序排列;
(3)比较a,$-b$,$-|c|$,$-(+d)$的大小;
(4)若有理数m满足$|b|<|m|$,试比较b,$-b$,m之间的大小关系.
(1)画出数轴,并标出表示数a,b,c,d的点的大致位置;
(2)将a,c,d,$-a$,$-c$,$-d$按照从小到大的顺序排列;
(3)比较a,$-b$,$-|c|$,$-(+d)$的大小;
(4)若有理数m满足$|b|<|m|$,试比较b,$-b$,m之间的大小关系.
答案:(1) (数轴略,大致位置从左到右为:-c,-b,d,a,-a,-d,b,c)
(2) 解:-c < d < a < -a < -d < c
(3) 解:-|c| < a < -(+d) < -b
(4) 解:当m为正数时,-b < b < m;当m为负数时,m < -b < b
(2) 解:-c < d < a < -a < -d < c
(3) 解:-|c| < a < -(+d) < -b
(4) 解:当m为正数时,-b < b < m;当m为负数时,m < -b < b
17. (2025·江苏盐城期末)若一个数的相反数比它本身大,则这个数一定是(
A.正数
B.整数
C.负数
D.非负数
C
)A.正数
B.整数
C.负数
D.非负数
答案:【解析】:
这个问题主要考查了相反数的性质和数的比较。
首先,设这个数为$x$,其相反数为$-x$。
根据题意,有不等式:$-x > x$。
将不等式两边同时加上$x$,得到:$0 > 2x$。
再将不等式两边同时除以2,得到:$0 > x$,即$x < 0$。
由此可知,这个数$x$一定是负数。
【答案】:
C. 负数。
这个问题主要考查了相反数的性质和数的比较。
首先,设这个数为$x$,其相反数为$-x$。
根据题意,有不等式:$-x > x$。
将不等式两边同时加上$x$,得到:$0 > 2x$。
再将不等式两边同时除以2,得到:$0 > x$,即$x < 0$。
由此可知,这个数$x$一定是负数。
【答案】:
C. 负数。
18. 亮点原创 已知正整数a,b满足$(|1+a|+|2-a|)(|b+2|+|b-1|)= 9$,则$a+2b= $
3或4
.答案:【解析】:
本题主要考查绝对值的性质和代数式的化简。
首先,我们考虑绝对值的性质。对于任意实数$x$,有:
$\begin{cases}x ,x \geq 0 \\ -x , x < 0\end{cases}$
对于$|1+a|$,当$a \geq -1$时,$|1+a| = 1+a$;当$a < -1$时,$|1+a| = -(1+a)$。
对于$|2-a|$,当$a \leq 2$时,$|2-a| = 2-a$;当$a > 2$时,$|2-a| = a-2$。
对于$|b+2|$,当$b \geq -2$时,$|b+2| = b+2$;当$b < -2$时,$|b+2| = -(b+2)$。
对于$|b-1|$,当$b \leq 1$时,$|b-1| = 1-b$;当$b > 1$时,$|b-1| = b-1$。
由于$a$和$b$都是正整数,我们可以得到以下结论:
$a \geq 1$(因为$a$是正整数),所以$|1+a| = 1+a$。
$a \leq 2$(保证$|2-a|$为正或0),所以$|2-a| = 2-a$。
$b \geq 1$(因为$b$是正整数且需要保证$|b-1|$为正或0),所以$|b+2| = b+2$,$|b-1| = b-1$。
将上述结论代入原式,得到:
$(1+a+2-a)(b+2+b-1) = 9$,
即:
$3(2b+1) = 9$,
解得:
$b = 1$,
再考虑$a$的取值,由于$a$是正整数且$a \leq 2$,所以$a$的可能取值为$1$或$2$。
当$a = 1$时,$a+2b = 1+2 × 1 = 3$;
当$a = 2$时,$a+2b = 2+2 × 1 = 4$。
【答案】:
3或4。
本题主要考查绝对值的性质和代数式的化简。
首先,我们考虑绝对值的性质。对于任意实数$x$,有:
$\begin{cases}x ,x \geq 0 \\ -x , x < 0\end{cases}$
对于$|1+a|$,当$a \geq -1$时,$|1+a| = 1+a$;当$a < -1$时,$|1+a| = -(1+a)$。
对于$|2-a|$,当$a \leq 2$时,$|2-a| = 2-a$;当$a > 2$时,$|2-a| = a-2$。
对于$|b+2|$,当$b \geq -2$时,$|b+2| = b+2$;当$b < -2$时,$|b+2| = -(b+2)$。
对于$|b-1|$,当$b \leq 1$时,$|b-1| = 1-b$;当$b > 1$时,$|b-1| = b-1$。
由于$a$和$b$都是正整数,我们可以得到以下结论:
$a \geq 1$(因为$a$是正整数),所以$|1+a| = 1+a$。
$a \leq 2$(保证$|2-a|$为正或0),所以$|2-a| = 2-a$。
$b \geq 1$(因为$b$是正整数且需要保证$|b-1|$为正或0),所以$|b+2| = b+2$,$|b-1| = b-1$。
将上述结论代入原式,得到:
$(1+a+2-a)(b+2+b-1) = 9$,
即:
$3(2b+1) = 9$,
解得:
$b = 1$,
再考虑$a$的取值,由于$a$是正整数且$a \leq 2$,所以$a$的可能取值为$1$或$2$。
当$a = 1$时,$a+2b = 1+2 × 1 = 3$;
当$a = 2$时,$a+2b = 2+2 × 1 = 4$。
【答案】:
3或4。
19. 新趋势 推导探究
【阅读材料】
我们知道,正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0.用字母表示如下:当$a>0$时,$|a|= a$;当$a<0$时,$|a|= -a$;当$a= 0$时,$|a|= 0$.在$a-b$中,若$a>b$,则$a-b>0$,$|a-b|= a-b$;若$a<b$,则$a-b<0$,$|a-b|= b-a$;若$a= b$,则$a-b= 0$,$|a-b|= 0$.
【解决问题】
(1)在$|x-1|$中,当$x>1$时,$x-1$
(2)在$|x-1|$中,当$x<1$时,$x-1$
(3)在$|x-1|$中,当$x= 1$时,$x-1$
(4)若数a,b,c在数轴上的位置如图所示,则$|b-a|= $
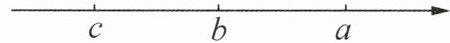
【阅读材料】
我们知道,正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0.用字母表示如下:当$a>0$时,$|a|= a$;当$a<0$时,$|a|= -a$;当$a= 0$时,$|a|= 0$.在$a-b$中,若$a>b$,则$a-b>0$,$|a-b|= a-b$;若$a<b$,则$a-b<0$,$|a-b|= b-a$;若$a= b$,则$a-b= 0$,$|a-b|= 0$.
【解决问题】
(1)在$|x-1|$中,当$x>1$时,$x-1$
>
0,$|x-1|= $$x - 1$
;(2)在$|x-1|$中,当$x<1$时,$x-1$
<
0,$|x-1|= $$1 - x$
;(3)在$|x-1|$中,当$x= 1$时,$x-1$
=
0,$|x-1|= $0
;(4)若数a,b,c在数轴上的位置如图所示,则$|b-a|= $
$a - b$
,$|b-c|= $$b - c$
.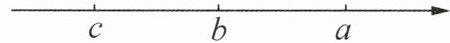
答案:【解析】:
(1) 当$x>1$时,根据绝对值的定义,$x-1$为正数,所以$|x-1|=x-1$,
(2) 当$x<1$时,$x-1$为负数,所以$|x-1|=1-x$,
(3) 当$x=1$时,$x-1=0$,所以$|x-1|=0$,
(4) 从数轴上的位置可以看出$c<b<a$,所以$b-a$为负数,$b-c$为正数,
根据绝对值的定义,负数的绝对值是它的相反数,正数的绝对值是它本身,
所以$|b-a|=a-b$,$|b-c|=b-c$,
【答案】:
(1) $>$;$x - 1$
(2) $<$;$1 - x$
(3) $=$;0
(4) $a - b$;$b - c$
(1) 当$x>1$时,根据绝对值的定义,$x-1$为正数,所以$|x-1|=x-1$,
(2) 当$x<1$时,$x-1$为负数,所以$|x-1|=1-x$,
(3) 当$x=1$时,$x-1=0$,所以$|x-1|=0$,
(4) 从数轴上的位置可以看出$c<b<a$,所以$b-a$为负数,$b-c$为正数,
根据绝对值的定义,负数的绝对值是它的相反数,正数的绝对值是它本身,
所以$|b-a|=a-b$,$|b-c|=b-c$,
【答案】:
(1) $>$;$x - 1$
(2) $<$;$1 - x$
(3) $=$;0
(4) $a - b$;$b - c$