11. 已知m是6的相反数,n比m的相反数小2,则$m-n+8= $
-2
.答案:解:因为m是6的相反数,所以$m = -6$。
m的相反数是$-m = 6$,n比m的相反数小2,所以$n = 6 - 2 = 4$。
则$m - n + 8 = -6 - 4 + 8 = -2$。
$-2$
m的相反数是$-m = 6$,n比m的相反数小2,所以$n = 6 - 2 = 4$。
则$m - n + 8 = -6 - 4 + 8 = -2$。
$-2$
12. 新素养抽象能力规定图形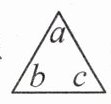 表示运算a-b+c,图形
表示运算a-b+c,图形 表示运算x+z-y-h,则
表示运算x+z-y-h,则 = ____
= ____
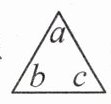 表示运算a-b+c,图形
表示运算a-b+c,图形 表示运算x+z-y-h,则
表示运算x+z-y-h,则 = ____
= ____4
.答案:【解析】:本题考查对新定义的运算规则的理解和有理数的加减混合运算。
首先,根据题目中给出的运算规则,将两个图形所代表的运算分别展开。
第一个图形$\begin{array}{r} 1\\ 2\ 3\end{array} $代表的运算是$1 - 2 + 3$。
第二个图形$\begin{bmatrix} 4&5\\ 7&6\end{bmatrix} $代表的运算是$4 + 6 - 7 - 5$。
然后,计算两个运算的结果。
第一个运算的结果是:$1 - 2 + 3 = 2$。
第二个运算的结果是:$4 + 6 - 7 - 5 = -2$。
最后,用第一个运算的结果减去第二个运算的结果,即$2 - (-2) = 2 + 2 = 4$。
【答案】:4
首先,根据题目中给出的运算规则,将两个图形所代表的运算分别展开。
第一个图形$\begin{array}{r} 1\\ 2\ 3\end{array} $代表的运算是$1 - 2 + 3$。
第二个图形$\begin{bmatrix} 4&5\\ 7&6\end{bmatrix} $代表的运算是$4 + 6 - 7 - 5$。
然后,计算两个运算的结果。
第一个运算的结果是:$1 - 2 + 3 = 2$。
第二个运算的结果是:$4 + 6 - 7 - 5 = -2$。
最后,用第一个运算的结果减去第二个运算的结果,即$2 - (-2) = 2 + 2 = 4$。
【答案】:4
13. (2025·江苏无锡期末)已知有理数+3,-8,-10,+12,请你通过有理数的加减混合运算,每个数只用一次,使得运算结果最大,则这个最大结果是
33
.答案:【解析】:
这个问题要求我们通过有理数的加减混合运算,使得结果最大。
给定的数有+3, -8, -10, +12。
为了使结果最大,我们应该尽量让正数相加,负数相减(即加上它们的绝对值)。
因为正数加正数会更大,负数减负数(即加上负数的绝对值)也会使结果增大。
所以,我们可以尝试将+3和+12相加,然后将-8和-10取反后相加,最后把两部分的结果相加。
具体计算如下:
$(+3) + (+12) - (-8) - (-10)$
$= 3 + 12 + 8 + 10$
$= 33$
【答案】:
33
这个问题要求我们通过有理数的加减混合运算,使得结果最大。
给定的数有+3, -8, -10, +12。
为了使结果最大,我们应该尽量让正数相加,负数相减(即加上它们的绝对值)。
因为正数加正数会更大,负数减负数(即加上负数的绝对值)也会使结果增大。
所以,我们可以尝试将+3和+12相加,然后将-8和-10取反后相加,最后把两部分的结果相加。
具体计算如下:
$(+3) + (+12) - (-8) - (-10)$
$= 3 + 12 + 8 + 10$
$= 33$
【答案】:
33
14. 计算:
(1)$-0.5-(-3\frac {1}{4})+2.75-(+7\frac {1}{2});$
(2)$(+1\frac {1}{2})-(-5)+(-\frac {1}{3})-(+\frac {1}{4})+(-5\frac {2}{3}).$
(1)$-0.5-(-3\frac {1}{4})+2.75-(+7\frac {1}{2});$
(2)$(+1\frac {1}{2})-(-5)+(-\frac {1}{3})-(+\frac {1}{4})+(-5\frac {2}{3}).$
答案:【解析】:
本题主要考查有理数的加减混合运算,需要掌握有理数加减法的运算规则和顺序。
(1) 对于第一个表达式,首先将所有数转换为假分数或小数形式,然后按照加减法运算规则进行计算。
(2) 对于第二个表达式,同样首先将所有数转换为假分数形式,并注意到有些数带有负号,需要按照加减法运算规则,特别是减去一个负数等于加上这个数的规则进行计算。
【答案】:
(1)
解:
原式
$= -0.5 - (-3.25) + 2.75 - 7.5$
$= -0.5 + 3.25 + 2.75 - 7.5$
$= (-0.5 - 7.5) + (3.25 + 2.75)$
$= -8 + 6$
$= -2$
(2)
解:
原式
$= 1\frac{1}{2} - (-5) - \frac{1}{3} - \frac{1}{4} - 5\frac{2}{3}$
$= 1\frac{1}{2} + 5 - \frac{1}{3} - \frac{1}{4} - 5\frac{2}{3}$
$= (1\frac{1}{2} + 5 - \frac{1}{4}) - (\frac{1}{3} + 5\frac{2}{3})$
$= 6\frac{1}{4} - 6$
$= \frac{1}{4}$
本题主要考查有理数的加减混合运算,需要掌握有理数加减法的运算规则和顺序。
(1) 对于第一个表达式,首先将所有数转换为假分数或小数形式,然后按照加减法运算规则进行计算。
(2) 对于第二个表达式,同样首先将所有数转换为假分数形式,并注意到有些数带有负号,需要按照加减法运算规则,特别是减去一个负数等于加上这个数的规则进行计算。
【答案】:
(1)
解:
原式
$= -0.5 - (-3.25) + 2.75 - 7.5$
$= -0.5 + 3.25 + 2.75 - 7.5$
$= (-0.5 - 7.5) + (3.25 + 2.75)$
$= -8 + 6$
$= -2$
(2)
解:
原式
$= 1\frac{1}{2} - (-5) - \frac{1}{3} - \frac{1}{4} - 5\frac{2}{3}$
$= 1\frac{1}{2} + 5 - \frac{1}{3} - \frac{1}{4} - 5\frac{2}{3}$
$= (1\frac{1}{2} + 5 - \frac{1}{4}) - (\frac{1}{3} + 5\frac{2}{3})$
$= 6\frac{1}{4} - 6$
$= \frac{1}{4}$
15. 新趋势情境素材某摩托车厂本周计划每日生产300辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况(增加的车辆数记为正数,减少的车辆数记为负数)如下表:
|星期|一|二|三|四|五|六|日|
|增减|-5|+7|-3|+4|+10|-9|-25|
(1)星期三生产了多少辆摩托车?
(2)本周总生产量与计划生产量相比,是增加还是减少? 相差多少辆?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
|星期|一|二|三|四|五|六|日|
|增减|-5|+7|-3|+4|+10|-9|-25|
(1)星期三生产了多少辆摩托车?
(2)本周总生产量与计划生产量相比,是增加还是减少? 相差多少辆?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
答案:【解析】:
(1) 星期三的生产量计算主要考察有理数的加减法。
根据题目,计划每日生产300辆,而星期三减少了3辆,所以实际生产量为$300 - 3 = 297$辆。
(2) 本周总生产量与计划生产量的比较,需要将每日的增减数量加起来,看总和是正数还是负数,以此来判断是增加还是减少,并计算出相差的数量。
(3) 产量最多的一天与产量最少的一天的比较,需要找出增减数量中的最大值和最小值,计算它们的差,以此来得出产量最多的一天比产量最少的一天多生产了多少辆。
【答案】:
(1) 解:星期三生产的摩托车数量为 $300 - 3 = 297$ 辆。
(2) 解:本周增减总数的计算如下:
$-5 + 7 - 3 + 4 + 10 - 9 - 25 = -21$
本周总生产量与计划生产量相比,减少了21辆。
(3) 解:产量最多的一天增加了10辆,而产量最少的一天减少了25辆。
所以,产量最多的一天比产量最少的一天多生产了 $10 - (-25) = 35$ 辆摩托车。
(1) 星期三的生产量计算主要考察有理数的加减法。
根据题目,计划每日生产300辆,而星期三减少了3辆,所以实际生产量为$300 - 3 = 297$辆。
(2) 本周总生产量与计划生产量的比较,需要将每日的增减数量加起来,看总和是正数还是负数,以此来判断是增加还是减少,并计算出相差的数量。
(3) 产量最多的一天与产量最少的一天的比较,需要找出增减数量中的最大值和最小值,计算它们的差,以此来得出产量最多的一天比产量最少的一天多生产了多少辆。
【答案】:
(1) 解:星期三生产的摩托车数量为 $300 - 3 = 297$ 辆。
(2) 解:本周增减总数的计算如下:
$-5 + 7 - 3 + 4 + 10 - 9 - 25 = -21$
本周总生产量与计划生产量相比,减少了21辆。
(3) 解:产量最多的一天增加了10辆,而产量最少的一天减少了25辆。
所以,产量最多的一天比产量最少的一天多生产了 $10 - (-25) = 35$ 辆摩托车。
16. 在前2025个正整数1,2,3,…,2025的每一个数前面都加上“+”号或“-”号,然后将它们相加,则所得的结果为 (
A.偶数
B.奇数
C.正数
D.负数
B
)A.偶数
B.奇数
C.正数
D.负数
答案:解:1到2025的正整数中,共有1013个奇数,1012个偶数。
因为奇数个奇数相加为奇数,偶数个偶数相加为偶数,奇数加偶数为奇数,所以1+2+3+…+2025的结果为奇数。
每个数前面加上“+”或“-”号,相当于在总和的基础上减去该数的2倍(若为“-”),2倍的数为偶数,奇数减去偶数仍为奇数。
故所得结果为奇数。
答案:B
因为奇数个奇数相加为奇数,偶数个偶数相加为偶数,奇数加偶数为奇数,所以1+2+3+…+2025的结果为奇数。
每个数前面加上“+”或“-”号,相当于在总和的基础上减去该数的2倍(若为“-”),2倍的数为偶数,奇数减去偶数仍为奇数。
故所得结果为奇数。
答案:B
17. 有一口水井,水面比井口低3m,一只蜗牛从水面沿井壁往井口爬,第一次往上爬了0.6m又下滑了0.1m,第二次往上爬了0.4m又下滑了0.15m,第三次往上爬了1.3m又下滑了0.2m,第四次往上爬了0.8m又下滑了0.3m,第五次往上爬了0.45m,则此时蜗牛爬出井口了吗?
答案:【解析】:
本题主要考察有理数的加减混合运算。根据题意,我们可以将蜗牛的每次爬升和下滑距离进行加减,以确定蜗牛是否爬出井口。
首先,我们列出蜗牛每次的爬升和下滑距离:
第一次:爬升$0.6m$,下滑$0.1m$;
第二次:爬升$0.4m$,下滑$0.15m$;
第三次:爬升$1.3m$,下滑$0.2m$;
第四次:爬升$0.8m$,下滑$0.3m$;
第五次:爬升$0.45m$,没有下滑。
接下来,我们进行有理数的加减混合运算,以确定蜗牛的最终位置:
$0.6 - 0.1 + 0.4 - 0.15 + 1.3 - 0.2 + 0.8 - 0.3 + 0.45 = 2.9m$
由于井的深度是$3m$,而蜗牛爬升的总高度是$2.9m$,因此我们可以得出结论。
【答案】:
蜗牛没有爬出井口。
本题主要考察有理数的加减混合运算。根据题意,我们可以将蜗牛的每次爬升和下滑距离进行加减,以确定蜗牛是否爬出井口。
首先,我们列出蜗牛每次的爬升和下滑距离:
第一次:爬升$0.6m$,下滑$0.1m$;
第二次:爬升$0.4m$,下滑$0.15m$;
第三次:爬升$1.3m$,下滑$0.2m$;
第四次:爬升$0.8m$,下滑$0.3m$;
第五次:爬升$0.45m$,没有下滑。
接下来,我们进行有理数的加减混合运算,以确定蜗牛的最终位置:
$0.6 - 0.1 + 0.4 - 0.15 + 1.3 - 0.2 + 0.8 - 0.3 + 0.45 = 2.9m$
由于井的深度是$3m$,而蜗牛爬升的总高度是$2.9m$,因此我们可以得出结论。
【答案】:
蜗牛没有爬出井口。
18. 一名足球守门员练习折返跑,从球门的位置出发,向前跑记作正数,往回跑记作负数,他的记录(单位:m)如下:+6,-4,+10,-7,+11,-6,-10.
(1)守门员是否回到了原来的位置?
(2)守门员离开球门的位置最远是多少米?
(3)守门员一共跑了多少米?
(1)守门员是否回到了原来的位置?
(2)守门员离开球门的位置最远是多少米?
(3)守门员一共跑了多少米?
答案:【解析】:
本题主要考察有理数的加减混合运算和绝对值的性质。
(1)为了判断守门员是否回到了原来的位置,我们需要计算他跑过的所有距离的总和。如果总和为0,则表示他回到了原点。
(2)为了找出守门员离开球门的最远位置,我们需要逐步累加他跑过的每一段距离,并记录下每一步的累计距离,然后找出这些累计距离中的最大值。
(3)为了计算守门员一共跑了多少米,我们需要求出他跑过的每一段距离的绝对值之和。
【答案】:
(1)守门员跑过的所有距离的总和为:
$( + 6) + ( - 4) + ( + 10) + ( - 7) + ( + 11) + ( - 6) + ( - 10) = 0$
由于总和为0,所以守门员回到了原来的位置。
(2)守门员每次跑后的累计距离为:
$6m, 6-4=2m, 2+10=12m, 12-7=5m, 5+11=16m, 16-6=10m, 10-10=0m$
其中,最大的累计距离是$16m$,所以守门员离开球门的位置最远是$16$米。
(3)守门员一共跑了多少米可以通过求他跑过的每一段距离的绝对值之和来得出:
$| + 6| + | - 4| + | + 10| + | - 7| + | + 11| + | - 6| + | - 10| = 54$
所以,守门员一共跑了$54$米。
本题主要考察有理数的加减混合运算和绝对值的性质。
(1)为了判断守门员是否回到了原来的位置,我们需要计算他跑过的所有距离的总和。如果总和为0,则表示他回到了原点。
(2)为了找出守门员离开球门的最远位置,我们需要逐步累加他跑过的每一段距离,并记录下每一步的累计距离,然后找出这些累计距离中的最大值。
(3)为了计算守门员一共跑了多少米,我们需要求出他跑过的每一段距离的绝对值之和。
【答案】:
(1)守门员跑过的所有距离的总和为:
$( + 6) + ( - 4) + ( + 10) + ( - 7) + ( + 11) + ( - 6) + ( - 10) = 0$
由于总和为0,所以守门员回到了原来的位置。
(2)守门员每次跑后的累计距离为:
$6m, 6-4=2m, 2+10=12m, 12-7=5m, 5+11=16m, 16-6=10m, 10-10=0m$
其中,最大的累计距离是$16m$,所以守门员离开球门的位置最远是$16$米。
(3)守门员一共跑了多少米可以通过求他跑过的每一段距离的绝对值之和来得出:
$| + 6| + | - 4| + | + 10| + | - 7| + | + 11| + | - 6| + | - 10| = 54$
所以,守门员一共跑了$54$米。