15. 计算:
(1)$-2^{3}÷(-3)^{2}$;
(2)$-(-3)^{2}×(-2)^{3}$;
(3)$(-0.25)^{3}×(-4)^{3}$.
(1)$-2^{3}÷(-3)^{2}$;
(2)$-(-3)^{2}×(-2)^{3}$;
(3)$(-0.25)^{3}×(-4)^{3}$.
答案:【解析】:
本题主要考查有理数的乘方运算及乘法与除法的运算规则。
(1) 对于 $-2^{3}÷(-3)^{2}$ ,首先计算乘方,再进行除法运算。
(2) 对于 $-(-3)^{2}×(-2)^{3}$ ,首先注意到负号在外,所以先计算括号内的乘方,再进行乘法运算,注意负负得正。
(3) 对于 $(-0.25)^{3}×(-4)^{3}$ ,首先分别计算两个数的乘方,再进行乘法运算,注意负负得正。
【答案】:
(1)
解:
$-2^{3} = -8$
$(-3)^{2} = 9$
所以,$-2^{3}÷(-3)^{2} = \frac{-8}{9} = -\frac{8}{9}$
(2)
解:
$(-3)^{2} = 9$
$(-2)^{3} = -8$
所以,$-(-3)^{2}×(-2)^{3} = -9 × (-8) = 72$
(3)
解:
$(-0.25)^{3} = -\frac{1}{64}$
$(-4)^{3} = -64$
但注意到,两个负数相乘结果为正,所以
$(-0.25)^{3}×(-4)^{3} = \left(-\frac{1}{64}\right) × (-64) = 1$
本题主要考查有理数的乘方运算及乘法与除法的运算规则。
(1) 对于 $-2^{3}÷(-3)^{2}$ ,首先计算乘方,再进行除法运算。
(2) 对于 $-(-3)^{2}×(-2)^{3}$ ,首先注意到负号在外,所以先计算括号内的乘方,再进行乘法运算,注意负负得正。
(3) 对于 $(-0.25)^{3}×(-4)^{3}$ ,首先分别计算两个数的乘方,再进行乘法运算,注意负负得正。
【答案】:
(1)
解:
$-2^{3} = -8$
$(-3)^{2} = 9$
所以,$-2^{3}÷(-3)^{2} = \frac{-8}{9} = -\frac{8}{9}$
(2)
解:
$(-3)^{2} = 9$
$(-2)^{3} = -8$
所以,$-(-3)^{2}×(-2)^{3} = -9 × (-8) = 72$
(3)
解:
$(-0.25)^{3} = -\frac{1}{64}$
$(-4)^{3} = -64$
但注意到,两个负数相乘结果为正,所以
$(-0.25)^{3}×(-4)^{3} = \left(-\frac{1}{64}\right) × (-64) = 1$
16. 为了求$1+3+3^{2}+3^{3}+…+3^{100}$的值,可令$M= 1+3+3^{2}+3^{3}+…+3^{100}$,则$3M= 3+3^{2}+3^{3}+3^{4}+…+3^{101}$,所以$3M-M= 3^{101}-1$,所以$M= \frac{3^{101}-1}{2}$,即$1+3+3^{2}+3^{3}+…+3^{100}= \frac{3^{101}-1}{2}$.仿照以上方法,求$1+5+5^{2}+5^{3}+…+5^{2025}$的值.
答案:【解析】:
题目考查了有理数的乘方以及等比数列求和的知识点。
题目中给出了一个等比数列的求和方法,即通过错位相减法来求解。
首先,我们设原式$S = 1+5+5^{2}+5^{3}+…+5^{2025}$,然后我们将原式两边同时乘以5,得到$5S = 5+5^{2}+5^{3}+5^{4}+…+5^{2026}$。
接着,我们将$5S$和$S$进行错位相减,即$5S - S = 5^{2026} - 1$,从而得到$4S = 5^{2026} - 1$。
最后,我们将等式两边同时除以4,得到$S = \frac{5^{2026} - 1}{4}$。
【答案】:
$1+5+5^{2}+5^{3}+…+5^{2025} = \frac{5^{2026} - 1}{4}$。
题目考查了有理数的乘方以及等比数列求和的知识点。
题目中给出了一个等比数列的求和方法,即通过错位相减法来求解。
首先,我们设原式$S = 1+5+5^{2}+5^{3}+…+5^{2025}$,然后我们将原式两边同时乘以5,得到$5S = 5+5^{2}+5^{3}+5^{4}+…+5^{2026}$。
接着,我们将$5S$和$S$进行错位相减,即$5S - S = 5^{2026} - 1$,从而得到$4S = 5^{2026} - 1$。
最后,我们将等式两边同时除以4,得到$S = \frac{5^{2026} - 1}{4}$。
【答案】:
$1+5+5^{2}+5^{3}+…+5^{2025} = \frac{5^{2026} - 1}{4}$。
17. 观察下列算式:$7^{1}= 7,7^{2}= 49,7^{3}= 343,7^{4}= 2401,7^{5}= 16807,…$.根据上述算式中的规律可知$7^{2025}$的个位数字是(
A.7
B.9
C.3
D.1
A
)A.7
B.9
C.3
D.1
答案:解:观察算式可得,$7^n$的个位数字依次为7、9、3、1循环出现,周期为4。
$2025÷4=506\cdots\cdots1$,其中余数为1。
所以$7^{2025}$的个位数字与$7^1$的个位数字相同,为7。
答案:A
$2025÷4=506\cdots\cdots1$,其中余数为1。
所以$7^{2025}$的个位数字与$7^1$的个位数字相同,为7。
答案:A
18. (2025·江苏徐州期末)阅读下面的材料,并解答问题.
一般地,$n个相同的因数a$相乘:$\underbrace{a\cdot a…\cdot \cdot a}_{n个a}记为a^{n}$,如:$2^{3}= 8$,此时3叫作以2为底8的对数,记为$\log_{2}8$(即$\log_{2}8= 3$).一般地,若$a^{n}= b(a>0且a≠1,b>0)$,则$n叫作以a为底b$的对数,记为$\log_{a}b$(即$\log_{a}b= n$),则$\log_{2}4,\log_{2}16,\log_{2}64$之间满足的关系式为
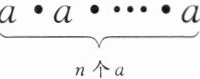
一般地,$n个相同的因数a$相乘:$\underbrace{a\cdot a…\cdot \cdot a}_{n个a}记为a^{n}$,如:$2^{3}= 8$,此时3叫作以2为底8的对数,记为$\log_{2}8$(即$\log_{2}8= 3$).一般地,若$a^{n}= b(a>0且a≠1,b>0)$,则$n叫作以a为底b$的对数,记为$\log_{a}b$(即$\log_{a}b= n$),则$\log_{2}4,\log_{2}16,\log_{2}64$之间满足的关系式为
$\log_{2}4+\log_{2}16=\log_{2}64$
.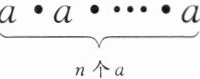
答案:【解析】:本题可根据对数的定义,分别求出$\log_{2}4$、$\log_{2}16$、$\log_{2}64$的值,再分析它们之间的关系。
根据对数的定义:若$a^{n}=b(a\gt0且a\neq1,b\gt0)$,则$\log_{a}b = n$。
对于$\log_{2}4$,因为$2^{2}=4$,所以$\log_{2}4 = 2$。
对于$\log_{2}16$,因为$2^{4}=16$,所以$\log_{2}16 = 4$。
对于$\log_{2}64$,因为$2^{6}=64$,所以$\log_{2}64 = 6$。
观察$2$、$4$、$6$这三个数,可发现$2 + 4 = 6$,即$\log_{2}4+\log_{2}16=\log_{2}64$。
【答案】:$\log_{2}4+\log_{2}16=\log_{2}64$
根据对数的定义:若$a^{n}=b(a\gt0且a\neq1,b\gt0)$,则$\log_{a}b = n$。
对于$\log_{2}4$,因为$2^{2}=4$,所以$\log_{2}4 = 2$。
对于$\log_{2}16$,因为$2^{4}=16$,所以$\log_{2}16 = 4$。
对于$\log_{2}64$,因为$2^{6}=64$,所以$\log_{2}64 = 6$。
观察$2$、$4$、$6$这三个数,可发现$2 + 4 = 6$,即$\log_{2}4+\log_{2}16=\log_{2}64$。
【答案】:$\log_{2}4+\log_{2}16=\log_{2}64$
19. 新趋势学科融合在生物学中,生物链中的能量流动有“逐级递减”的特点,一个营养级中的能量只有$10\%~20\%$能被下一个营养级所利用.在如图所示的生物链中($H_{n}表示第n$营养级),若$H_{1}$中输入了1000千焦能量,流动过程中每一个营养级中只有$10\%$的能量被下一营养级所利用,求$H_{4}$获得的能量.
$H_{1}→H_{2}→H_{3}→H_{4}$
$H_{1}→H_{2}→H_{3}→H_{4}$
答案:【解析】:
本题考察的是有理数的乘方运算。
根据题目描述,每一个营养级中只有$10%$的能量被下一营养级所利用。
因此,从$H_{1}$到$H_{2}$,能量变为$1000 × 10\%$;
从$H_{2}$到$H_{3}$,能量再变为$1000 × (10\%)^{2}$;
从$H_{3}$到$H_{4}$,能量继续变为$1000 × (10\%)^{3}$。
这实际上是一个连续的乘法运算,每次乘以$10%$,即乘以$0.1$。
所以,$H_{4}$获得的能量为$1000 × (0.1)^{3}$千焦。
【答案】:
解:$H_{4}$获得的能量为
$1000 × (10\%)^{3} = 1000 × (0.1)^{3} = 1000 × 0.001 = 1$(千焦)。
答:$H_{4}$获得的能量为$1$千焦。
本题考察的是有理数的乘方运算。
根据题目描述,每一个营养级中只有$10%$的能量被下一营养级所利用。
因此,从$H_{1}$到$H_{2}$,能量变为$1000 × 10\%$;
从$H_{2}$到$H_{3}$,能量再变为$1000 × (10\%)^{2}$;
从$H_{3}$到$H_{4}$,能量继续变为$1000 × (10\%)^{3}$。
这实际上是一个连续的乘法运算,每次乘以$10%$,即乘以$0.1$。
所以,$H_{4}$获得的能量为$1000 × (0.1)^{3}$千焦。
【答案】:
解:$H_{4}$获得的能量为
$1000 × (10\%)^{3} = 1000 × (0.1)^{3} = 1000 × 0.001 = 1$(千焦)。
答:$H_{4}$获得的能量为$1$千焦。
20. 我们常用的数是十进制数,计算机程序使用的数是二进制数(只有数字0和1),它们两者之间可以互相换算,如将$(101)_{2},(1011)_{2}$换算成十进制数结果如下:$(101)_{2}= 1×2^{2}+0×2^{1}+1= 4+0+1= 5$;$(1011)_{2}= 1×2^{3}+0×2^{2}+1×2^{1}+1= 8+0+2+1= 11$.按此方式,将二进制数$(1001)_{2}$换算成十进制数是多少?
答案:【解析】:
题目考查了二进制与十进制的换算,具体是将二进制数转换为十进制数。
根据题目给出的换算方式,需要将二进制数的每一位与2的对应次方相乘,然后求和。
对于二进制数$(1001)_{2}$,从右到左的位数对应的2的次方分别是$2^{0}$、$2^{1}$、$2^{2}$、$2^{3}$。
根据二进制转十进制的方法,计算过程为:
$1 × 2^{3} + 0 × 2^{2} + 0 × 2^{1} + 1 × 2^{0}$
$= 8 + 0 + 0 + 1$
$= 9$
【答案】:
9
题目考查了二进制与十进制的换算,具体是将二进制数转换为十进制数。
根据题目给出的换算方式,需要将二进制数的每一位与2的对应次方相乘,然后求和。
对于二进制数$(1001)_{2}$,从右到左的位数对应的2的次方分别是$2^{0}$、$2^{1}$、$2^{2}$、$2^{3}$。
根据二进制转十进制的方法,计算过程为:
$1 × 2^{3} + 0 × 2^{2} + 0 × 2^{1} + 1 × 2^{0}$
$= 8 + 0 + 0 + 1$
$= 9$
【答案】:
9