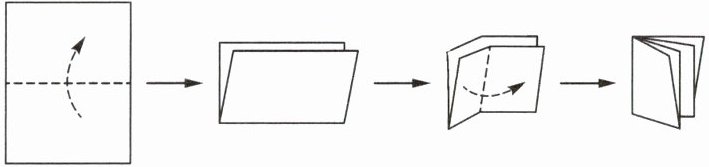
7. 新素养 几何直观 将一张长方形纸片按如图所示的方式折成一个小长方形,压平后用剪刀沿小长方形的一条对角线剪开,则展开后纸片的张数是______.

4或5
答案:4或5
8. 如图①为某月的月历,根据月历上的信息,解答下列问题:
(1) 如图②,若十字框中间的数为 a,则十字框中 5 个数的和为
(2) 小李一家外出游玩了 5 天.若这 5 天的日期之和为 75,则他们是
(3) 在该月历上用十字框框出 5 个数,能使这 5 个数的和为 100 吗? 若不能,请说明理由;若能,请求出十字框中间的数.
解:不能。理由如下:
设十字框中间的数为a,由(1)知5个数的和为5a。
令5a=100,解得a=20。
由图①可知,20在月历最右侧,其右边没有数字,无法构成十字框,故不能。
(1) 如图②,若十字框中间的数为 a,则十字框中 5 个数的和为
5a
;(用含a 的式子表示)(2) 小李一家外出游玩了 5 天.若这 5 天的日期之和为 75,则他们是
13
日外出的;(3) 在该月历上用十字框框出 5 个数,能使这 5 个数的和为 100 吗? 若不能,请说明理由;若能,请求出十字框中间的数.
解:不能。理由如下:
设十字框中间的数为a,由(1)知5个数的和为5a。
令5a=100,解得a=20。
由图①可知,20在月历最右侧,其右边没有数字,无法构成十字框,故不能。
答案:(1) 5a
(2) 13
(3) 解:不能。理由如下:
设十字框中间的数为a,由(1)知5个数的和为5a。
令5a=100,解得a=20。
由图①可知,20在月历最右侧,其右边没有数字,无法构成十字框,故不能。
(2) 13
(3) 解:不能。理由如下:
设十字框中间的数为a,由(1)知5个数的和为5a。
令5a=100,解得a=20。
由图①可知,20在月历最右侧,其右边没有数字,无法构成十字框,故不能。
9. 将三张大小相同的正方形卡片 A,B,C 叠放在一个底面为正方形的盒底上,将底面未被卡片覆盖的部分涂上阴影.按图①所示方式摆放时,阴影部分的面积为$S_{1}$;按图②所示方式摆放时,阴影部分的面积为$S_{2}$,则$S_{1}$
=
$S_{2}$.(填“>”“<”或“=”)答案:【解析】:本题可通过设未知数,分别表示出两种摆放方式下阴影部分的面积,再比较它们的大小。
设大正方形的边长为$a$,小正方形的边长为$b$。
在图①中,阴影部分是由两个长方形组成,这两个长方形的长分别为$a - b$,宽为$b$,根据长方形面积公式$S = 长×宽$,可得阴影部分面积$S_{1}=b(a - b)+(a - b)b = 2b(a - b)=2ab - 2b^{2}$。
在图②中,阴影部分同样是由两个长方形组成,这两个长方形的长分别为$a - b$,宽为$b$,所以阴影部分面积$S_{2}=b(a - b)+(a - b)b = 2b(a - b)=2ab - 2b^{2}$。
比较$S_{1}$与$S_{2}$的大小,因为$S_{1}=2ab - 2b^{2}$,$S_{2}=2ab - 2b^{2}$,所以$S_{1}=S_{2}$。
【答案】:=
设大正方形的边长为$a$,小正方形的边长为$b$。
在图①中,阴影部分是由两个长方形组成,这两个长方形的长分别为$a - b$,宽为$b$,根据长方形面积公式$S = 长×宽$,可得阴影部分面积$S_{1}=b(a - b)+(a - b)b = 2b(a - b)=2ab - 2b^{2}$。
在图②中,阴影部分同样是由两个长方形组成,这两个长方形的长分别为$a - b$,宽为$b$,所以阴影部分面积$S_{2}=b(a - b)+(a - b)b = 2b(a - b)=2ab - 2b^{2}$。
比较$S_{1}$与$S_{2}$的大小,因为$S_{1}=2ab - 2b^{2}$,$S_{2}=2ab - 2b^{2}$,所以$S_{1}=S_{2}$。
【答案】:=
10. 新素养 推理能力 推理能力都很强的甲、乙、丙三人站成一列,丙可以看见甲、乙,乙可以看见甲但看不见丙,甲看不见乙、丙.现有 5 顶帽子,3 顶白色,2 顶黑色.老师分别给每人戴上一顶帽子(在各自不知道的情况下).老师先问丙是否知道自己头上的帽子颜色,丙回答说不知道;老师再问乙是否知道自己头上的帽子颜色,乙也回答说不知道;老师最后问甲是否知道自己头上的帽子颜色,甲回答说知道.请你说出甲戴了什么颜色的帽子,并写出推理过程.
答案:【解析】:
这是一个逻辑推理题,主要考察的是如何通过给定的信息来推断出未知的信息。题目描述了三个人和他们的可视关系以及他们头上的帽子颜色。我们需要根据他们是否能看见其他人的帽子颜色以及他们的回答来推断出甲头上的帽子颜色。
首先,我们明确题目给出的条件:
1. 三人中,丙可以看见甲、乙,乙可以看见甲但看不见丙,甲看不见乙、丙。
2. 共有5顶帽子,其中3顶是白色,2顶是黑色。
3. 当老师问及每个人头上的帽子颜色时,丙和乙都表示不知道,而甲表示知道。
接下来,我们根据这些条件进行推理:
1. 如果丙看到甲和乙头上都戴的是黑帽子,那么丙肯定知道自己戴的是白帽子(因为只有2顶黑帽子)。但丙回答说不知道,说明他看到的情况并非如此。所以,甲和乙头上的帽子颜色组合不可能是两顶黑帽子。
2. 如果乙看到甲戴的是黑帽子,并且考虑到上述丙的推理,乙就能确定自己戴的是白帽子(因为如果甲戴黑帽子,丙就能确定自己戴白帽子,但丙说不知道,说明甲没戴黑帽子或者乙戴白帽子,而乙能看到甲,所以如果甲戴黑帽子,乙就能确定自己戴白帽子)。但乙也回答说不知道,说明他看到甲戴的并非黑帽子。
3. 综上所述,甲头上戴的只能是白帽子。因为如果是黑帽子,乙和丙中至少有一个人能确定自己帽子的颜色,但他们都说不知道。
【答案】:
甲戴了白色的帽子。推理过程如上所述。
这是一个逻辑推理题,主要考察的是如何通过给定的信息来推断出未知的信息。题目描述了三个人和他们的可视关系以及他们头上的帽子颜色。我们需要根据他们是否能看见其他人的帽子颜色以及他们的回答来推断出甲头上的帽子颜色。
首先,我们明确题目给出的条件:
1. 三人中,丙可以看见甲、乙,乙可以看见甲但看不见丙,甲看不见乙、丙。
2. 共有5顶帽子,其中3顶是白色,2顶是黑色。
3. 当老师问及每个人头上的帽子颜色时,丙和乙都表示不知道,而甲表示知道。
接下来,我们根据这些条件进行推理:
1. 如果丙看到甲和乙头上都戴的是黑帽子,那么丙肯定知道自己戴的是白帽子(因为只有2顶黑帽子)。但丙回答说不知道,说明他看到的情况并非如此。所以,甲和乙头上的帽子颜色组合不可能是两顶黑帽子。
2. 如果乙看到甲戴的是黑帽子,并且考虑到上述丙的推理,乙就能确定自己戴的是白帽子(因为如果甲戴黑帽子,丙就能确定自己戴白帽子,但丙说不知道,说明甲没戴黑帽子或者乙戴白帽子,而乙能看到甲,所以如果甲戴黑帽子,乙就能确定自己戴白帽子)。但乙也回答说不知道,说明他看到甲戴的并非黑帽子。
3. 综上所述,甲头上戴的只能是白帽子。因为如果是黑帽子,乙和丙中至少有一个人能确定自己帽子的颜色,但他们都说不知道。
【答案】:
甲戴了白色的帽子。推理过程如上所述。