1. 如图,一串有趣的动物图案按一定规律排列,请仔细观察,猜想第2025个图案是(
C
)答案:【解析】:
本题可先找出这串动物图案的排列规律,再根据规律计算出第$2025$个图案是什么。
观察这串动物图案可知,这些图案是以“兔子、猴子、海马、海豚”这$4$个图案为一组依次循环出现的。
要求第$2025$个图案是什么,可通过计算$2025$除以每组图案的个数$4$,根据所得的余数来判断。
具体计算过程为:用$2025$除以$4$,得到商和余数,商表示一共有多少组完整的图案,余数表示在第$2025$个图案时,是下一组的第几个图案。
若余数为$1$,则对应兔子;若余数为$2$,则对应猴子;若余数为$3$,则对应海马;若余数为$0$,则对应海豚。
【答案】:
解:$2025÷4 = 506\cdots\cdots1$
其中$506$是商,$1$是余数。
这意味着到第$2025$个图案时,一共有$506$组完整的“兔子、猴子、海马、海豚”图案,余数为$1$,说明第$2025$个图案是下一组的第$1$个图案,即兔子。
所以答案选C。
本题可先找出这串动物图案的排列规律,再根据规律计算出第$2025$个图案是什么。
观察这串动物图案可知,这些图案是以“兔子、猴子、海马、海豚”这$4$个图案为一组依次循环出现的。
要求第$2025$个图案是什么,可通过计算$2025$除以每组图案的个数$4$,根据所得的余数来判断。
具体计算过程为:用$2025$除以$4$,得到商和余数,商表示一共有多少组完整的图案,余数表示在第$2025$个图案时,是下一组的第几个图案。
若余数为$1$,则对应兔子;若余数为$2$,则对应猴子;若余数为$3$,则对应海马;若余数为$0$,则对应海豚。
【答案】:
解:$2025÷4 = 506\cdots\cdots1$
其中$506$是商,$1$是余数。
这意味着到第$2025$个图案时,一共有$506$组完整的“兔子、猴子、海马、海豚”图案,余数为$1$,说明第$2025$个图案是下一组的第$1$个图案,即兔子。
所以答案选C。
2. 下列图形都是由完全相同的小梯形按一定规律组成的.易知第1个图形的周长为5,那么第2025个图形的周长为(
A.6074
B.6077
C.6080
D.6083
B
)A.6074
B.6077
C.6080
D.6083
答案:【解析】:本题可先根据图形找出其周长随图形序号变化的规律,再根据规律求出第$2025$个图形的周长。
步骤一:分析前几个图形的周长,找出规律
第$1$个图形:由图可知,其周长为$5$,可表示为$2 + 3×1 = 5$。
第$2$个图形:观察可得,其周长为$8$,可表示为$2 + 3×2 = 8$。
第$3$个图形:其周长为$11$,可表示为$2 + 3×3 = 11$。
通过以上分析,可以总结出规律:第$n$个图形的周长为$2 + 3n$。
步骤二:根据规律求出第$2025$个图形的周长
将$n = 2025$代入到$2 + 3n$中,可得:
$2 + 3×2025 = 2 + 6075 = 6077$
【答案】:B
步骤一:分析前几个图形的周长,找出规律
第$1$个图形:由图可知,其周长为$5$,可表示为$2 + 3×1 = 5$。
第$2$个图形:观察可得,其周长为$8$,可表示为$2 + 3×2 = 8$。
第$3$个图形:其周长为$11$,可表示为$2 + 3×3 = 11$。
通过以上分析,可以总结出规律:第$n$个图形的周长为$2 + 3n$。
步骤二:根据规律求出第$2025$个图形的周长
将$n = 2025$代入到$2 + 3n$中,可得:
$2 + 3×2025 = 2 + 6075 = 6077$
【答案】:B
3. 新素养 推理能力 观察下列各式:$1\frac{1}{2},2\frac{1}{4},3\frac{1}{8},4\frac{1}{16},…$,则第6项是
$6\frac{1}{64}$
.答案:解:观察可得,整数部分依次为1,2,3,4,…,第n项的整数部分为n;分数部分的分母依次为2,4,8,16,…,即$2^1$,$2^2$,$2^3$,$2^4$,…,第n项分数部分的分母为$2^n$,分子均为1。
所以第6项的整数部分为6,分数部分为$\frac{1}{2^6}=\frac{1}{64}$,则第6项是$6\frac{1}{64}$。
答案:$6\frac{1}{64}$
所以第6项的整数部分为6,分数部分为$\frac{1}{2^6}=\frac{1}{64}$,则第6项是$6\frac{1}{64}$。
答案:$6\frac{1}{64}$
4. (教材P9练习变式)如图,图案①中有4个三角形,图案②中有6个三角形,图案③中有8个三角形,…$$,按此规律排列,图案⑦中三角形的个数为
16
.答案:【解析】:
观察图案中三角形的个数:
图案①中有$4$个三角形,
图案②中有$6$个三角形,
图案③中有$8$个三角形。
可以发现每个图案比前一个图案多$2$个三角形。
设图案编号为$n$,图案中三角形的个数为$a_n$。
根据观察,可以得出以下规律:
$a_1=4$,
$a_2=6=4+2×(2-1)$,
$a_3=8=4+2×(3-1)$,
由此可以推断出一般公式:
$a_n=4+2×(n-1)=2n+2$。
将$n=7$代入公式,得到:
$a_7=2×7+2=16$。
【答案】:
$16$。
观察图案中三角形的个数:
图案①中有$4$个三角形,
图案②中有$6$个三角形,
图案③中有$8$个三角形。
可以发现每个图案比前一个图案多$2$个三角形。
设图案编号为$n$,图案中三角形的个数为$a_n$。
根据观察,可以得出以下规律:
$a_1=4$,
$a_2=6=4+2×(2-1)$,
$a_3=8=4+2×(3-1)$,
由此可以推断出一般公式:
$a_n=4+2×(n-1)=2n+2$。
将$n=7$代入公式,得到:
$a_7=2×7+2=16$。
【答案】:
$16$。
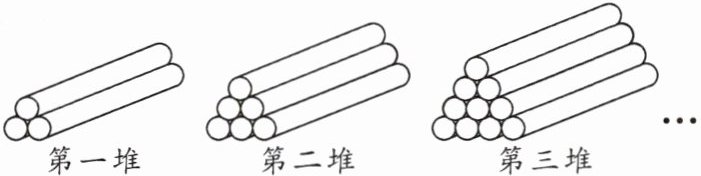
5. 木材加工厂堆放木料的方式如图所示,依此规律,求第六堆木料的根数.

答案:【解析】:
本题主要考查了图形的变化规律,通过观察每堆木料的根数,发现它们之间的数量关系,进而推导出一般公式来求解特定堆数的木料根数,涉及到找规律和代数运算的知识点。
观察图形可知:
第一堆木料的根数为:$1+2=3$(根);
第二堆木料的根数为:$1+2+3=6$(根);
第三堆木料的根数为:$1+2+3+4=10$(根);
以此类推,第$n$堆木料的根数为:$1+2+3+\cdots +(n + 1)$。
根据等差数列求和公式$S_n=\frac{n(a_1+a_n)}{2}$(其中$n$为项数,$a_1$为首项,$a_n$为末项),对于$1+2+3+\cdots +(n + 1)$,首项$a_1 = 1$,末项$a_n=n + 1$,项数为$n + 1$,则其和为$\frac{(n + 1)(1 + n + 1)}{2}=\frac{(n + 1)(n + 2)}{2}$。
要求第六堆木料的根数,将$n = 6$代入上述公式可得:$\frac{(6 + 1)×(6 + 2)}{2}=\frac{7×8}{2}=28$(根)。
【答案】:
第六堆木料的根数是$28$根。
本题主要考查了图形的变化规律,通过观察每堆木料的根数,发现它们之间的数量关系,进而推导出一般公式来求解特定堆数的木料根数,涉及到找规律和代数运算的知识点。
观察图形可知:
第一堆木料的根数为:$1+2=3$(根);
第二堆木料的根数为:$1+2+3=6$(根);
第三堆木料的根数为:$1+2+3+4=10$(根);
以此类推,第$n$堆木料的根数为:$1+2+3+\cdots +(n + 1)$。
根据等差数列求和公式$S_n=\frac{n(a_1+a_n)}{2}$(其中$n$为项数,$a_1$为首项,$a_n$为末项),对于$1+2+3+\cdots +(n + 1)$,首项$a_1 = 1$,末项$a_n=n + 1$,项数为$n + 1$,则其和为$\frac{(n + 1)(1 + n + 1)}{2}=\frac{(n + 1)(n + 2)}{2}$。
要求第六堆木料的根数,将$n = 6$代入上述公式可得:$\frac{(6 + 1)×(6 + 2)}{2}=\frac{7×8}{2}=28$(根)。
【答案】:
第六堆木料的根数是$28$根。
6. 仔细观察如图所示的三个图形,依此规律,第四个图形为(
B
)答案:【解析】:本题主要考查观察图形规律的能力。
观察前三个图形,发现每个图形都是在前一个图形的基础上,在相交形成的新的区域内添加一条线段,同时新图形的最外层五角星的边与相邻的内部五角星的边所形成的区域内添加阴影,且阴影部分不重复。
第一个图形有1条阴影,第二个图形有2条阴影,第三个图形有3条阴影,依此类推,第四个图形应该有4条阴影。
根据上述规律,对选项进行逐一分析:
A选项:图形中有3条阴影,不符合第四个图形应该有4条阴影的规律,所以A选项错误。
B选项:图形中有4条阴影,且符合在相交形成的新的区域内添加一条线段,同时新图形的最外层五角星的边与相邻的内部五角星的边所形成的区域内添加阴影,且阴影部分不重复的规律,所以B选项正确。
C选项:图形中有3条阴影,不符合第四个图形应该有4条阴影的规律,所以C选项错误。
D选项:图形中有5条阴影,不符合第四个图形应该有4条阴影的规律,所以D选项错误。
【答案】:B
观察前三个图形,发现每个图形都是在前一个图形的基础上,在相交形成的新的区域内添加一条线段,同时新图形的最外层五角星的边与相邻的内部五角星的边所形成的区域内添加阴影,且阴影部分不重复。
第一个图形有1条阴影,第二个图形有2条阴影,第三个图形有3条阴影,依此类推,第四个图形应该有4条阴影。
根据上述规律,对选项进行逐一分析:
A选项:图形中有3条阴影,不符合第四个图形应该有4条阴影的规律,所以A选项错误。
B选项:图形中有4条阴影,且符合在相交形成的新的区域内添加一条线段,同时新图形的最外层五角星的边与相邻的内部五角星的边所形成的区域内添加阴影,且阴影部分不重复的规律,所以B选项正确。
C选项:图形中有3条阴影,不符合第四个图形应该有4条阴影的规律,所以C选项错误。
D选项:图形中有5条阴影,不符合第四个图形应该有4条阴影的规律,所以D选项错误。
【答案】:B
7. 有一串神秘排列的数:1,1,2,3,5,8,…$$,则第10个数是(
A.34
B.44
C.55
D.89
C
)A.34
B.44
C.55
D.89
答案:【解析】:
这个问题考查的是对斐波那契数列的理解和应用。斐波那契数列是这样一个数列:前两个数都是1,从第三个数开始,每个数都是前两个数的和。即F(1)=1,F(2)=1,F(n)=F(n-1)+F(n-2)(n>2)。
根据斐波那契数列的定义,我们可以依次计算出数列的每一项,直到找到第10个数。
【答案】:
首先,我们列出斐波那契数列的前几项:
F(1) = 1,
F(2) = 1,
F(3) = F(2) + F(1) = 2,
F(4) = F(3) + F(2) = 3,
F(5) = F(4) + F(3) = 5,
F(6) = F(5) + F(4) = 8,
F(7) = F(6) + F(5) = 13,
F(8) = F(7) + F(6) = 21,
F(9) = F(8) + F(7) = 34,
F(10) = F(9) + F(8) = 55。
所以,第10个数是55,故选C。
这个问题考查的是对斐波那契数列的理解和应用。斐波那契数列是这样一个数列:前两个数都是1,从第三个数开始,每个数都是前两个数的和。即F(1)=1,F(2)=1,F(n)=F(n-1)+F(n-2)(n>2)。
根据斐波那契数列的定义,我们可以依次计算出数列的每一项,直到找到第10个数。
【答案】:
首先,我们列出斐波那契数列的前几项:
F(1) = 1,
F(2) = 1,
F(3) = F(2) + F(1) = 2,
F(4) = F(3) + F(2) = 3,
F(5) = F(4) + F(3) = 5,
F(6) = F(5) + F(4) = 8,
F(7) = F(6) + F(5) = 13,
F(8) = F(7) + F(6) = 21,
F(9) = F(8) + F(7) = 34,
F(10) = F(9) + F(8) = 55。
所以,第10个数是55,故选C。
8. 观察下面一列数:$1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6},…$,探究其中的规律,解答下面的问题:
(1)这列数的第12个数是
(2)这列数无限排列下去,越来越接近的数是
(1)这列数的第12个数是
$\frac{1}{12}$
,第2025个数是$\frac{1}{2025}$
;(2)这列数无限排列下去,越来越接近的数是
0
.答案:【解析】:
(1) 观察数列 $1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6},\ldots$,
可以发现数列的规律是第 $n$ 个数为 $\frac{1}{n}$。
根据这个规律,第 12 个数就是 $\frac{1}{12}$,第 2025 个数就是 $\frac{1}{2025}$。
(2) 对于数列无限排列下去的情况,
由于数列的每一项都是其位置的倒数,当位置趋于无穷大时,数值将趋于 0。
因此,这列数无限排列下去,越来越接近的数是 0。
【答案】:
(1) $\frac{1}{12}$;$\frac{1}{2025}$
(2) 0
(1) 观察数列 $1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\frac{1}{6},\ldots$,
可以发现数列的规律是第 $n$ 个数为 $\frac{1}{n}$。
根据这个规律,第 12 个数就是 $\frac{1}{12}$,第 2025 个数就是 $\frac{1}{2025}$。
(2) 对于数列无限排列下去的情况,
由于数列的每一项都是其位置的倒数,当位置趋于无穷大时,数值将趋于 0。
因此,这列数无限排列下去,越来越接近的数是 0。
【答案】:
(1) $\frac{1}{12}$;$\frac{1}{2025}$
(2) 0