9. 新素养 推理能力 如图为手的示意图,在各个手指间标记字母A,B,C,D,请你按图中箭头所指方向($A\to B\to C\to D\to C\to B\to A\to B\to C…$)从字母A开始数连续的正整数1,2,3,4,…$$,当数到12时,对应的字母是
B
;当字母C第201次出现时,恰好数到的数是603
.答案:解:观察数的顺序与字母对应关系:1-A,2-B,3-C,4-D,5-C,6-B,7-A,8-B,9-C,10-D,11-C,12-B,…,可得周期为6(A,B,C,D,C,B)。
12÷6=2,余数为0,对应周期最后一个字母B。
每个周期中字母C出现2次(第3、5位)。201÷2=100(个周期)……1(次),前100个周期数到6×100=600,第201次C为下周期第3位,600+3=603。
答案:B;603
12÷6=2,余数为0,对应周期最后一个字母B。
每个周期中字母C出现2次(第3、5位)。201÷2=100(个周期)……1(次),前100个周期数到6×100=600,第201次C为下周期第3位,600+3=603。
答案:B;603
10. 观察下面一列数:$-1,2,-3,4,-5,6,-7,…$,将这列数排成如图所示的三角形数阵.按照此规律排下去,解答下列问题:
(1)第10行从左边数第9个数是多少?
(2)从左边数,-2025是第几行第几个数?
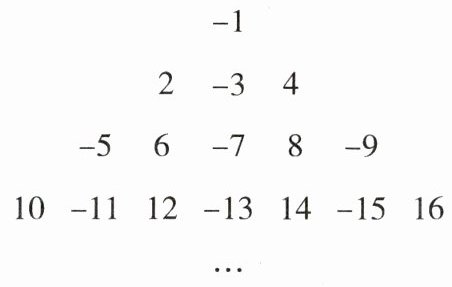
(1)第10行从左边数第9个数是多少?
(2)从左边数,-2025是第几行第几个数?
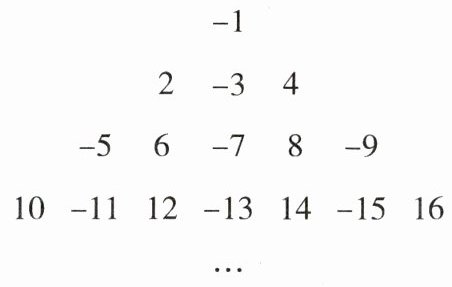
答案:(1) 解:前9行共有数字:$1+3+5+\cdots+(2×9-1)=9^2=81$(个),第10行从左边数第9个数是第$81+9=90$个数,符号为正,故这个数是90。
(2) 解:$\because45^2=2025$,$\therefore$第45行共有$2×45-1=89$个数,前44行共有$44^2=1936$个数,$2025-1936=89$,故-2025是第45行第89个数。
(2) 解:$\because45^2=2025$,$\therefore$第45行共有$2×45-1=89$个数,前44行共有$44^2=1936$个数,$2025-1936=89$,故-2025是第45行第89个数。
11. 如图,各正方形中的四个数之间都有相同的规律,根据此规律,x的值为(
A.181
B.217
C.219
D.199
D
)A.181
B.217
C.219
D.199
答案:解:观察前三个正方形,左上角数字依次为1,2,3,规律为n(n为第n个正方形);右上角数字依次为1,3,5,规律为2n-1;左下角数字依次为2,3,4,规律为n+1。
第四个正方形右上角数字为19,由2n-1=19,得n=10。
则左上角a=n=10,左下角b=n+1=11。
前三个正方形右下角数字规律:1=1×2-1,7=2×3+1(修正:1=1×1+0,7=2×3+1,17=3×5+2,实际应为右上角×左下角+左上角:1×2+(-1)错误,重新观察:1=1×1+0,7=2×3+1,17=3×5+2,0,1,2为n-1,故17=3×5+2=3×5+(3-1),验证7=2×3+1=2×3+(2-1),1=1×1+0=1×1+(1-1),所以右下角=左上角×右上角+(左上角-1)。
x=a×19+(a-1)=10×19+9=199。
答案:D
第四个正方形右上角数字为19,由2n-1=19,得n=10。
则左上角a=n=10,左下角b=n+1=11。
前三个正方形右下角数字规律:1=1×2-1,7=2×3+1(修正:1=1×1+0,7=2×3+1,17=3×5+2,实际应为右上角×左下角+左上角:1×2+(-1)错误,重新观察:1=1×1+0,7=2×3+1,17=3×5+2,0,1,2为n-1,故17=3×5+2=3×5+(3-1),验证7=2×3+1=2×3+(2-1),1=1×1+0=1×1+(1-1),所以右下角=左上角×右上角+(左上角-1)。
x=a×19+(a-1)=10×19+9=199。
答案:D
12. 甲、乙、丙、丁四名同学围成一圈依序循环报数.规定:①甲、乙、丙、丁首次报出的数依次为1,2,3,4,接着甲报5,乙报6,…$$,每名同学报出的数比前一名同学报出的数大1,按此规律,当报出的数是50时,报数结束;②若报出的数是3的倍数,则报该数的同学需拍手一次.在此过程中,甲同学需拍
4
次手.答案:【解析】:
本题主要考查了数字的变化规律与有余数的除法。
首先,根据题目描述,甲、乙、丙、丁四名同学围成一圈依序循环报数,且报出的数依次递增。
因此,可以确定甲同学报的数构成一个等差数列,其中首项为1,公差为4(因为每次循环报数,甲都间隔3个人后再次报数)。
接下来,需要找出甲同学报的所有数中,哪些是3的倍数。
由于甲同学报的数构成等差数列,可以通过计算找出这些数。
设甲同学第$n$次报的数为$a_n$,则有:
$a_n = 1 + 4(n - 1) = 4n - 3$,
为了找出3的倍数,可以将$a_n$除以3,并观察余数:
$a_n \mod 3 = (4n - 3) \mod 3 = (n + 0) \mod 3$,
当$n$除以3的余数为0时(即$n = 3k, k \in \mathbb{N}^*$),$a_n$是3的倍数。
但是,由于我们的起始数是1,不是3的倍数,
所以需要从$n=3k-2$(即实际报数时的第$3k-2$次)开始考虑,
这样甲报的数才会是3的倍数(因为$4(3k-2) - 3 = 12k - 11$,而$12k$是3的倍数,$-11 \equiv 1 \pmod{3}$,
所以$4(3k-2) - 3 \equiv 1 - 3 \equiv -2 \equiv 1 \pmod{3}$的下一个即$4(3k-1) - 3 = 12k - 7 \equiv -1 \equiv 2 \pmod{3}$的下一个$4 × 3k - 3 = 12k - 3$才是3的倍数)。
经过调整,我们得到当$n = 3k - 2$($k$为正整数)时,
对应的报数$a_{3k - 2} = 4(3k - 2) - 3 = 12k - 11$(但这个表达式在直接除以3时不是3的倍数,
我们需要的是其下一个数,即$k$增加1后的数)或直接从$n$的表达式出发,
考虑甲报的数中3的倍数的实际位置,为$n = 3k - 1$(因为从$n=1$开始,每3个数中,第2个是3的倍数,
对应到$n$上就是$3k-1$),
此时$a_{3k - 1} = 4(3k - 1) - 3 = 12k - 4 - 3 = 12k - 7$(但这个可以由$n$的表达式直接推导出,
且更关注$n$的取值),
实际上应直接考虑报数序列中甲报的数,
即$a_n$中$n$取何值时$a_n$是3的倍数,
由$a_n = 4n - 3$,
令$4n - 3 = 3m$($m$为正整数),
解得$n = \frac{3m + 3}{4} = \frac{3(m + 1)}{4}$,
由于$n$必须是正整数,
所以$m+1$必须是4的倍数,
即$m = 4k - 1$($k$为正整数),
此时$n = 3k - 1$。
现在,需要找出在报数到50的过程中,甲同学报了多少次3的倍数。
由于甲同学报的数构成等差数列,且公差为4,
因此可以通过不等式找出满足条件的$k$的取值范围:
$1 \leq 4(3k - 1) - 3 \leq 50$,
$1 \leq 12k - 4 - 3 \leq 50$,
$1 \leq 12k - 7 \leq 50$,
$8 \leq 12k \leq 57$,
$\frac{2}{3} \leq k \leq \frac{19}{4}$,
由于$k$必须是正整数,
因此$k$的取值为$1, 2, 3, 4$。
所以,甲同学在报数过程中需要拍手的次数为4次(对应$k=1, 2, 3, 4$)。
但这里需要注意,我们的起始数调整是基于直接观察报数序列得出的,
而直接通过$n$的表达式计算时,应直接考虑$n=3k-1$的形式,
并验证其对应的报数确实是3的倍数(如上面通过$m=4k-1$推导出的$n=3k-1$)。
因此,最终甲同学需要拍手的次数就是满足条件的$k$的个数,即4次。
但考虑到直接通过报数序列验证,
我们可以列出甲同学报的数:1, 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, 49。
其中9, 21, 33, 45是3的倍数,共4次。
【答案】:
4
本题主要考查了数字的变化规律与有余数的除法。
首先,根据题目描述,甲、乙、丙、丁四名同学围成一圈依序循环报数,且报出的数依次递增。
因此,可以确定甲同学报的数构成一个等差数列,其中首项为1,公差为4(因为每次循环报数,甲都间隔3个人后再次报数)。
接下来,需要找出甲同学报的所有数中,哪些是3的倍数。
由于甲同学报的数构成等差数列,可以通过计算找出这些数。
设甲同学第$n$次报的数为$a_n$,则有:
$a_n = 1 + 4(n - 1) = 4n - 3$,
为了找出3的倍数,可以将$a_n$除以3,并观察余数:
$a_n \mod 3 = (4n - 3) \mod 3 = (n + 0) \mod 3$,
当$n$除以3的余数为0时(即$n = 3k, k \in \mathbb{N}^*$),$a_n$是3的倍数。
但是,由于我们的起始数是1,不是3的倍数,
所以需要从$n=3k-2$(即实际报数时的第$3k-2$次)开始考虑,
这样甲报的数才会是3的倍数(因为$4(3k-2) - 3 = 12k - 11$,而$12k$是3的倍数,$-11 \equiv 1 \pmod{3}$,
所以$4(3k-2) - 3 \equiv 1 - 3 \equiv -2 \equiv 1 \pmod{3}$的下一个即$4(3k-1) - 3 = 12k - 7 \equiv -1 \equiv 2 \pmod{3}$的下一个$4 × 3k - 3 = 12k - 3$才是3的倍数)。
经过调整,我们得到当$n = 3k - 2$($k$为正整数)时,
对应的报数$a_{3k - 2} = 4(3k - 2) - 3 = 12k - 11$(但这个表达式在直接除以3时不是3的倍数,
我们需要的是其下一个数,即$k$增加1后的数)或直接从$n$的表达式出发,
考虑甲报的数中3的倍数的实际位置,为$n = 3k - 1$(因为从$n=1$开始,每3个数中,第2个是3的倍数,
对应到$n$上就是$3k-1$),
此时$a_{3k - 1} = 4(3k - 1) - 3 = 12k - 4 - 3 = 12k - 7$(但这个可以由$n$的表达式直接推导出,
且更关注$n$的取值),
实际上应直接考虑报数序列中甲报的数,
即$a_n$中$n$取何值时$a_n$是3的倍数,
由$a_n = 4n - 3$,
令$4n - 3 = 3m$($m$为正整数),
解得$n = \frac{3m + 3}{4} = \frac{3(m + 1)}{4}$,
由于$n$必须是正整数,
所以$m+1$必须是4的倍数,
即$m = 4k - 1$($k$为正整数),
此时$n = 3k - 1$。
现在,需要找出在报数到50的过程中,甲同学报了多少次3的倍数。
由于甲同学报的数构成等差数列,且公差为4,
因此可以通过不等式找出满足条件的$k$的取值范围:
$1 \leq 4(3k - 1) - 3 \leq 50$,
$1 \leq 12k - 4 - 3 \leq 50$,
$1 \leq 12k - 7 \leq 50$,
$8 \leq 12k \leq 57$,
$\frac{2}{3} \leq k \leq \frac{19}{4}$,
由于$k$必须是正整数,
因此$k$的取值为$1, 2, 3, 4$。
所以,甲同学在报数过程中需要拍手的次数为4次(对应$k=1, 2, 3, 4$)。
但这里需要注意,我们的起始数调整是基于直接观察报数序列得出的,
而直接通过$n$的表达式计算时,应直接考虑$n=3k-1$的形式,
并验证其对应的报数确实是3的倍数(如上面通过$m=4k-1$推导出的$n=3k-1$)。
因此,最终甲同学需要拍手的次数就是满足条件的$k$的个数,即4次。
但考虑到直接通过报数序列验证,
我们可以列出甲同学报的数:1, 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45, 49。
其中9, 21, 33, 45是3的倍数,共4次。
【答案】:
4
13. 新趋势 推导探究 【阅读材料】高斯上小学时,有一次数学老师让同学们计算“从1到100这100个正整数的和”.许多同学都采用了依次累加的计算方法,计算起来非常繁琐,且易出错.聪明的高斯经过探索后,给出了下面的解答过程:设$S= 1+2+3+…+100$①,则$S= 100+99+98+…+1$②.①+②,得$2S= (1+100)+(2+99)+(3+98)+…+(100+1)= 100×101$,所以$S= \frac{100×101}{2}$,即$1+2+3+…+100= 5050$.后来人们将高斯的这种解答方法概括为“倒序相加法”.
【解决问题】利用“倒序相加法”,解答下列问题:
(1)计算:$1+2+3+…+20= $
(2)计算:$101+102+…+200$.
【解决问题】利用“倒序相加法”,解答下列问题:
(1)计算:$1+2+3+…+20= $
210
;(2)计算:$101+102+…+200$.
15050
答案:【解析】:
(1) 设$S = 1 + 2 + 3 + \ldots + 20$ ①,
同样地,我们可以将序列倒序写出,即$S = 20 + 19 + 18 + \ldots + 1$ ②,
将①和②相加,得到$2S = (1 + 20) + (2 + 19) + (3 + 18) + \ldots + (20 + 1) = 20 × 21$,
所以,$S = \frac{20 × 21}{2} = 210$。
(2) 对于$101 + 102 + \ldots + 200$,我们可以先考虑$1 + 2 + \ldots + 200$的和,再减去$1 + 2 + \ldots + 100$的和。
设$S_1 = 1 + 2 + 3 + \ldots + 200$,
倒序后$S_1 = 200 + 199 + 198 + \ldots + 1$,
两式相加得$2S_1 = (1 + 200) + (2 + 199) + \ldots + (200 + 1) = 200 × 201$,
所以,$S_1 = \frac{200 × 201}{2} = 20100$。
再考虑$S_2 = 1 + 2 + 3 + \ldots + 100$,由(1)的解答,我们知道$S_2 = 5050$。
因此,$101 + 102 + \ldots + 200 = S_1 - S_2 = 20100 - 5050 = 15050$。
【答案】:
(1) $210$
(2) $15050$
(1) 设$S = 1 + 2 + 3 + \ldots + 20$ ①,
同样地,我们可以将序列倒序写出,即$S = 20 + 19 + 18 + \ldots + 1$ ②,
将①和②相加,得到$2S = (1 + 20) + (2 + 19) + (3 + 18) + \ldots + (20 + 1) = 20 × 21$,
所以,$S = \frac{20 × 21}{2} = 210$。
(2) 对于$101 + 102 + \ldots + 200$,我们可以先考虑$1 + 2 + \ldots + 200$的和,再减去$1 + 2 + \ldots + 100$的和。
设$S_1 = 1 + 2 + 3 + \ldots + 200$,
倒序后$S_1 = 200 + 199 + 198 + \ldots + 1$,
两式相加得$2S_1 = (1 + 200) + (2 + 199) + \ldots + (200 + 1) = 200 × 201$,
所以,$S_1 = \frac{200 × 201}{2} = 20100$。
再考虑$S_2 = 1 + 2 + 3 + \ldots + 100$,由(1)的解答,我们知道$S_2 = 5050$。
因此,$101 + 102 + \ldots + 200 = S_1 - S_2 = 20100 - 5050 = 15050$。
【答案】:
(1) $210$
(2) $15050$