1. 在数轴上, 与表示数 -5 的点的距离为 2 的点表示的数是 (
A.-3
B.-7
C.$\pm 3$
D.-3 或 -7
D
)A.-3
B.-7
C.$\pm 3$
D.-3 或 -7
答案:【解析】:
本题考查了数轴上两点间的距离知识。在数轴上,与某一点距离为d的点有两个,一个在该点的左边,一个在该点的右边,距离均为d。因此,与表示数-5的点距离为2的点有两个,一个在-5的左边2个单位长度处,表示的数为$-5-2=-7$;一个在-5的右边2个单位长度处,表示的数为$-5+2=-3$。
【答案】:
D. -3 或 -7
本题考查了数轴上两点间的距离知识。在数轴上,与某一点距离为d的点有两个,一个在该点的左边,一个在该点的右边,距离均为d。因此,与表示数-5的点距离为2的点有两个,一个在-5的左边2个单位长度处,表示的数为$-5-2=-7$;一个在-5的右边2个单位长度处,表示的数为$-5+2=-3$。
【答案】:
D. -3 或 -7
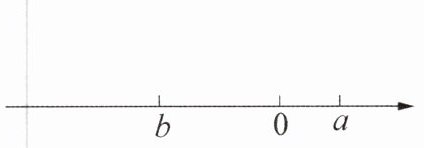
2. 新素养 几何直观 已知有理数 a, b 在数轴上的位置如图所示, 则下列关系正确的是 (
A.$|a|>|b|$
B.$a>-b$
C.$b<-a$
D.$a+b>0$
C
)
A.$|a|>|b|$
B.$a>-b$
C.$b<-a$
D.$a+b>0$
答案:解:由数轴可知,$b < 0 < a$,且$|b| > |a|$。
A. $|a| < |b|$,故A错误;
B. 因为$|b| > |a|$,所以$-b > a$,即$a < -b$,故B错误;
C. 因为$-b > a > 0$,所以$b < -a$,故C正确;
D. $a + b < 0$,故D错误。
答案:C
A. $|a| < |b|$,故A错误;
B. 因为$|b| > |a|$,所以$-b > a$,即$a < -b$,故B错误;
C. 因为$-b > a > 0$,所以$b < -a$,故C正确;
D. $a + b < 0$,故D错误。
答案:C
3. 如图, 数轴上标出若干个点, 每相邻两点之间相距 1 个单位长度, 点 A, B, C, D 表示的数分别是整数 a, b, c, d, 且 $d - 2a = 10$, 则数轴的原点是 (
A.点 A
B.点 B
C.点 C
D.点 D
B
)A.点 A
B.点 B
C.点 C
D.点 D
答案:【解析】:
首先,我们根据题目条件设点A表示的数为$a$,由于每相邻两点之间相距1个单位长度,所以点B,C,D分别表示的数为$a+3$,$a+5$,$a+7$(通过观察数轴,我们可以得出这些关系)。
接着,我们利用给定的条件$d - 2a = 10$,将$d$替换为$a+7$,得到方程:
$a + 7 - 2a = 10$
解这个方程,我们可以得到$a = -3$。
然后,我们可以找出数轴上各个点表示的数:
点A表示的数为$a = -3$,
点B表示的数为$a+3 = 0$,
点C表示的数为$a+5 = 2$,
点D表示的数为$a+7 = 4$。
由于原点表示的数是0,所以我们可以确定原点是点B。
【答案】:B
首先,我们根据题目条件设点A表示的数为$a$,由于每相邻两点之间相距1个单位长度,所以点B,C,D分别表示的数为$a+3$,$a+5$,$a+7$(通过观察数轴,我们可以得出这些关系)。
接着,我们利用给定的条件$d - 2a = 10$,将$d$替换为$a+7$,得到方程:
$a + 7 - 2a = 10$
解这个方程,我们可以得到$a = -3$。
然后,我们可以找出数轴上各个点表示的数:
点A表示的数为$a = -3$,
点B表示的数为$a+3 = 0$,
点C表示的数为$a+5 = 2$,
点D表示的数为$a+7 = 4$。
由于原点表示的数是0,所以我们可以确定原点是点B。
【答案】:B
4. 若 $|a| = 19$, $|b| = 97$, 且 $|a + b| \neq a + b$, 则 $a - b$ 的值是 (
A.-78 或 116
B.78 或 116
C.-78 或 -116
D.78 或 -1
B
)A.-78 或 116
B.78 或 116
C.-78 或 -116
D.78 或 -1
答案:解:
∵|a|=19,|b|=97,
∴a=±19,b=±97.
∵|a+b|≠a+b,
∴a+b<0.
情况1: 当a=19时,
19+b<0 ⇒ b<-19.
∵b=±97,∴b=-97.
此时a-b=19-(-97)=116.
情况2: 当a=-19时,
-19+b<0 ⇒ b<19.
∵b=±97,∴b=-97.
此时a-b=-19-(-97)=78.
综上,a-b=78或116.
答案:B
∵|a|=19,|b|=97,
∴a=±19,b=±97.
∵|a+b|≠a+b,
∴a+b<0.
情况1: 当a=19时,
19+b<0 ⇒ b<-19.
∵b=±97,∴b=-97.
此时a-b=19-(-97)=116.
情况2: 当a=-19时,
-19+b<0 ⇒ b<19.
∵b=±97,∴b=-97.
此时a-b=-19-(-97)=78.
综上,a-b=78或116.
答案:B
5. 已知有理数 a, b, c 在数轴上的位置如图所示. 试化简: $|a + c| + |b - c| - |a - b|$.
答案:【解析】:
首先,根据数轴上的位置,可以确定$a$,$b$,$c$之间的大小关系。
由数轴可知,$a \lt c \lt 0 \lt b$,且$|a| \gt |c|$,$|b| \lt |c|$。
根据这些关系,可以判断以下表达式的正负:
$a + c \lt 0$,因为$a$和$c$都是负数,且$|a| \gt |c|$。
$b - c \gt 0$,因为$b$是正数,$c$是负数。
$a - b \lt 0$,因为$a$是负数,$b$是正数。
根据绝对值的定义,正数的绝对值是它本身,负数的绝对值是它的相反数,可以得到:
$|a + c| = -(a + c)$
$|b - c| = b - c$
$|a - b| = -(a - b) = b - a$
将上述结果代入原式,得到:
$|a + c| + |b - c| - |a - b| = -(a + c) + (b - c) - (b - a) = -a - c + b - c - b + a = -2c$
【答案】:
$-2c$
首先,根据数轴上的位置,可以确定$a$,$b$,$c$之间的大小关系。
由数轴可知,$a \lt c \lt 0 \lt b$,且$|a| \gt |c|$,$|b| \lt |c|$。
根据这些关系,可以判断以下表达式的正负:
$a + c \lt 0$,因为$a$和$c$都是负数,且$|a| \gt |c|$。
$b - c \gt 0$,因为$b$是正数,$c$是负数。
$a - b \lt 0$,因为$a$是负数,$b$是正数。
根据绝对值的定义,正数的绝对值是它本身,负数的绝对值是它的相反数,可以得到:
$|a + c| = -(a + c)$
$|b - c| = b - c$
$|a - b| = -(a - b) = b - a$
将上述结果代入原式,得到:
$|a + c| + |b - c| - |a - b| = -(a + c) + (b - c) - (b - a) = -a - c + b - c - b + a = -2c$
【答案】:
$-2c$
6. 已知 $|x| = 3$, $|y| = 2$.
(1) 当 $xy < 0$ 时, 求 $x + y$ 的值;
(2) 求 $x - y$ 的最大值.
(1) 当 $xy < 0$ 时, 求 $x + y$ 的值;
(2) 求 $x - y$ 的最大值.
答案:【解析】:
本题主要考察绝对值的性质和有理数的运算。
(1) 由于 $|x| = 3$ 和 $|y| = 2$,根据绝对值的定义,$x$ 可以取 $\pm 3$,$y$ 可以取 $\pm 2$。
又因为 $xy < 0$,即 $x$ 和 $y$ 必须异号。
因此,有两种情况:$x = 3, y = -2$ 或 $x = -3, y = 2$。
对于第一种情况,$x + y = 3 + (-2) = 1$;
对于第二种情况,$x + y = -3 + 2 = -1$。
(2) 要求 $x - y$ 的最大值,我们需要考虑 $x$ 和 $y$ 的所有可能组合。
当 $x = 3, y = 2$ 时,$x - y = 3 - 2 = 1$;
当 $x = 3, y = -2$ 时,$x - y = 3 - (-2) = 5$;
当 $x = -3, y = 2$ 时,$x - y = -3 - 2 = -5$;
当 $x = -3, y = -2$ 时,$x - y = -3 - (-2) = -1$。
因此,$x - y$ 的最大值是 $5$。
【答案】:
(1) $x + y = \pm 1$;
(2) $x - y$ 的最大值是 $5$。
本题主要考察绝对值的性质和有理数的运算。
(1) 由于 $|x| = 3$ 和 $|y| = 2$,根据绝对值的定义,$x$ 可以取 $\pm 3$,$y$ 可以取 $\pm 2$。
又因为 $xy < 0$,即 $x$ 和 $y$ 必须异号。
因此,有两种情况:$x = 3, y = -2$ 或 $x = -3, y = 2$。
对于第一种情况,$x + y = 3 + (-2) = 1$;
对于第二种情况,$x + y = -3 + 2 = -1$。
(2) 要求 $x - y$ 的最大值,我们需要考虑 $x$ 和 $y$ 的所有可能组合。
当 $x = 3, y = 2$ 时,$x - y = 3 - 2 = 1$;
当 $x = 3, y = -2$ 时,$x - y = 3 - (-2) = 5$;
当 $x = -3, y = 2$ 时,$x - y = -3 - 2 = -5$;
当 $x = -3, y = -2$ 时,$x - y = -3 - (-2) = -1$。
因此,$x - y$ 的最大值是 $5$。
【答案】:
(1) $x + y = \pm 1$;
(2) $x - y$ 的最大值是 $5$。
7. (2025·江苏无锡期末) 若 $|x - 1| + |y + 2| + |z - 3| = 0$, 则 $(x + 1)(y - 2)(z + 3)$ 的值是 (
A.48
B.-48
C.0
D.24
B
)A.48
B.-48
C.0
D.24
答案:【解析】:
本题主要考察绝对值的性质和代数表达式的求值。
由于绝对值函数的输出总是非负的,即 $|a| \geq 0$,那么 $|x - 1| + |y + 2| + |z - 3| = 0$ 只有在每一项都等于0的情况下才成立。
因此,我们可以得到以下三个方程:
$x - 1 = 0$,解得 $x = 1$
$y + 2 = 0$,解得 $y = -2$
$z - 3 = 0$,解得 $z = 3$
将解得的 $x, y, z$ 值代入 $(x + 1)(y - 2)(z + 3)$,我们得到:
$(1 + 1)((-2) - 2)(3 + 3) = 2 × (-4) × 6 = -48$
【答案】:B
本题主要考察绝对值的性质和代数表达式的求值。
由于绝对值函数的输出总是非负的,即 $|a| \geq 0$,那么 $|x - 1| + |y + 2| + |z - 3| = 0$ 只有在每一项都等于0的情况下才成立。
因此,我们可以得到以下三个方程:
$x - 1 = 0$,解得 $x = 1$
$y + 2 = 0$,解得 $y = -2$
$z - 3 = 0$,解得 $z = 3$
将解得的 $x, y, z$ 值代入 $(x + 1)(y - 2)(z + 3)$,我们得到:
$(1 + 1)((-2) - 2)(3 + 3) = 2 × (-4) × 6 = -48$
【答案】:B
8. (2025·江苏淮安期末) 已知有理数 a, b 满足 $|ab - 2| + |a - 1| = 0$, 求 $\frac{1}{ab} + \frac{1}{(a + 1)(b + 1)} + \frac{1}{(a + 2)(b + 2)} + … + \frac{1}{(a + 2025)(b + 2025)}$ 的值.
答案:【解析】:
本题主要考查了绝对值的非负性以及代数式的化简与求值。
由于绝对值的非负性,有 $|ab - 2| \geq 0$ 和 $|a - 1| \geq 0$。
给定 $|ab - 2| + |a - 1| = 0$,由于绝对值非负,这意味着 $|ab - 2| = 0$ 和 $|a - 1| = 0$。
解这两个方程,得到 $ab - 2 = 0$ 和 $a - 1 = 0$。
解得 $a = 1$,$b = 2$。
将 $a$ 和 $b$ 的值代入原式,得到:
$\frac{1}{1 × 2} + \frac{1}{2 × 3} + \frac{1}{3 × 4} + \ldots + \frac{1}{2026 × 2027}$
这是一个等差数列的求和问题,可以使用裂项法来化简:
$= (1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + \ldots + (\frac{1}{2026} - \frac{1}{2027})$
$= 1 - \frac{1}{2027}$
$= \frac{2026}{2027}$
【答案】:
$\frac{2026}{2027}$
本题主要考查了绝对值的非负性以及代数式的化简与求值。
由于绝对值的非负性,有 $|ab - 2| \geq 0$ 和 $|a - 1| \geq 0$。
给定 $|ab - 2| + |a - 1| = 0$,由于绝对值非负,这意味着 $|ab - 2| = 0$ 和 $|a - 1| = 0$。
解这两个方程,得到 $ab - 2 = 0$ 和 $a - 1 = 0$。
解得 $a = 1$,$b = 2$。
将 $a$ 和 $b$ 的值代入原式,得到:
$\frac{1}{1 × 2} + \frac{1}{2 × 3} + \frac{1}{3 × 4} + \ldots + \frac{1}{2026 × 2027}$
这是一个等差数列的求和问题,可以使用裂项法来化简:
$= (1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{3} - \frac{1}{4}) + \ldots + (\frac{1}{2026} - \frac{1}{2027})$
$= 1 - \frac{1}{2027}$
$= \frac{2026}{2027}$
【答案】:
$\frac{2026}{2027}$
9. 如图, 在数轴上, 点 A 表示的数为 1, 现将点 A 沿数轴做如下移动: 第一次将点 A 向左移动 3 个单位长度到点 $A_1$, 第二次将点 $A_1$ 向右移动 6 个单位长度到点 $A_2$, 第三次将点 $A_2$ 向左移动 9 个单位长度到点 $A_3$, …$$, 按照这种规律移动, 第 n 次移动到点 $A_n$. 若点 $A_n$ 与原点的距离不小于 20, 则 n 的最小值为 ______.


13
答案:【解析】:本题主要考查数轴上点的移动规律以及绝对值的应用,通过分析点$A$每次移动的单位长度和方向,找出移动规律,进而得出点$A_n$所表示的数的表达式,最后根据点$A_n$与原点的距离不小于$20$列出不等式求解$n$的最小值。
步骤一:分析点$A$每次移动后所表示的数
已知点$A$表示的数为$1$,第一次将点$A$向左移动$3$个单位长度到点$A_1$,根据数轴上点向左移动数值减小,可得点$A_1$表示的数为$1 - 3 = -2$。
第二次将点$A_1$向右移动$6$个单位长度到点$A_2$,根据数轴上点向右移动数值增大,可得点$A_2$表示的数为$-2 + 6 = 4$。
第三次将点$A_2$向左移动$9$个单位长度到点$A_3$,可得点$A_3$表示的数为$4 - 9 = -5$。
第四次将点$A_3$向右移动$12$个单位长度到点$A_4$,可得点$A_4$表示的数为$-5 + 12 = 7$。
$\cdots$
步骤二:找出移动规律并得出点$A_n$所表示的数的表达式
当$n$为奇数时,点$A_n$表示的数为$1 + (-3) + 6 + (-9) + 12 + \cdots + (-1)^{n}× 3n$。
将相邻两项看作一组,每组的计算结果为$3$,一共有$\frac{n - 1}{2}$组,再加上第一项$1$,可得点$A_n$表示的数为$1 + 3×\frac{n - 1}{2} - 3n = -\frac{3n + 1}{2}$。
当$n$为偶数时,点$A_n$表示的数为$1 + (-3) + 6 + (-9) + 12 + \cdots + (-1)^{n}× 3n$。
同样将相邻两项看作一组,每组的计算结果为$3$,一共有$\frac{n}{2}$组,可得点$A_n$表示的数为$1 + 3×\frac{n}{2} = \frac{3n + 2}{2}$。
步骤三:根据点$A_n$与原点的距离不小于$20$列出不等式并求解$n$的最小值
当$n$为奇数时,$\vert -\frac{3n + 1}{2}\vert\geq 20$,即$\frac{3n + 1}{2}\geq 20$,
$3n + 1\geq 40$,
$3n\geq 39$,
解得$n\geq 13$,因为$13$是奇数,符合条件。
当$n$为偶数时,$\vert \frac{3n + 2}{2}\vert\geq 20$,即$\frac{3n + 2}{2}\geq 20$,
$3n + 2\geq 40$,
$3n\geq 38$,
解得$n\geq \frac{38}{3}\approx 12.67$,因为$n$为偶数,所以$n$的最小值为$14$。
比较$13$和$14$的大小,可得$13\lt 14$,所以$n$的最小值为$13$。
【答案】:$13$
步骤一:分析点$A$每次移动后所表示的数
已知点$A$表示的数为$1$,第一次将点$A$向左移动$3$个单位长度到点$A_1$,根据数轴上点向左移动数值减小,可得点$A_1$表示的数为$1 - 3 = -2$。
第二次将点$A_1$向右移动$6$个单位长度到点$A_2$,根据数轴上点向右移动数值增大,可得点$A_2$表示的数为$-2 + 6 = 4$。
第三次将点$A_2$向左移动$9$个单位长度到点$A_3$,可得点$A_3$表示的数为$4 - 9 = -5$。
第四次将点$A_3$向右移动$12$个单位长度到点$A_4$,可得点$A_4$表示的数为$-5 + 12 = 7$。
$\cdots$
步骤二:找出移动规律并得出点$A_n$所表示的数的表达式
当$n$为奇数时,点$A_n$表示的数为$1 + (-3) + 6 + (-9) + 12 + \cdots + (-1)^{n}× 3n$。
将相邻两项看作一组,每组的计算结果为$3$,一共有$\frac{n - 1}{2}$组,再加上第一项$1$,可得点$A_n$表示的数为$1 + 3×\frac{n - 1}{2} - 3n = -\frac{3n + 1}{2}$。
当$n$为偶数时,点$A_n$表示的数为$1 + (-3) + 6 + (-9) + 12 + \cdots + (-1)^{n}× 3n$。
同样将相邻两项看作一组,每组的计算结果为$3$,一共有$\frac{n}{2}$组,可得点$A_n$表示的数为$1 + 3×\frac{n}{2} = \frac{3n + 2}{2}$。
步骤三:根据点$A_n$与原点的距离不小于$20$列出不等式并求解$n$的最小值
当$n$为奇数时,$\vert -\frac{3n + 1}{2}\vert\geq 20$,即$\frac{3n + 1}{2}\geq 20$,
$3n + 1\geq 40$,
$3n\geq 39$,
解得$n\geq 13$,因为$13$是奇数,符合条件。
当$n$为偶数时,$\vert \frac{3n + 2}{2}\vert\geq 20$,即$\frac{3n + 2}{2}\geq 20$,
$3n + 2\geq 40$,
$3n\geq 38$,
解得$n\geq \frac{38}{3}\approx 12.67$,因为$n$为偶数,所以$n$的最小值为$14$。
比较$13$和$14$的大小,可得$13\lt 14$,所以$n$的最小值为$13$。
【答案】:$13$