10. 一种每件价格为$m$元的商品,甲超市连续两次打八折,乙超市一次性打六折,丙超市第一次打七折,第二次再打九折。若顾客要购买这种商品,则最划算的是去(
A.甲超市
B.乙超市
C.丙超市
D.乙超市或丙超市
B
)A.甲超市
B.乙超市
C.丙超市
D.乙超市或丙超市
答案:解:甲超市:$m×0.8×0.8 = 0.64m$
乙超市:$m×0.6 = 0.6m$
丙超市:$m×0.7×0.9 = 0.63m$
因为$0.6m < 0.63m < 0.64m$,所以最划算的是乙超市。
答案:B
乙超市:$m×0.6 = 0.6m$
丙超市:$m×0.7×0.9 = 0.63m$
因为$0.6m < 0.63m < 0.64m$,所以最划算的是乙超市。
答案:B
11. 新素养几何直观图中阴影部分的面积是(
A.$ad + c(b - d)$
B.$c(b - d) + d(a - c)$
C.$ab + bc$
D.$ab - cd$
]
A
)A.$ad + c(b - d)$
B.$c(b - d) + d(a - c)$
C.$ab + bc$
D.$ab - cd$
]
答案:解:阴影部分可分割为两个长方形。左侧长方形长为$a$,宽为$d$,面积为$ad$;右侧长方形长为$c$,宽为$(b - d)$,面积为$c(b - d)$。总面积为$ad + c(b - d)$。
答案:A
答案:A
12. (2025·江苏宿迁期末)某国家森林公园门票的价格为成人票每张30元,儿童票每张15元。若购买$m张成人票和n$张儿童票,则共需花费
$30m + 15n$
元。答案:【解析】:
这个问题是一个代数表达式问题,需要我们将文字描述转化为数学表达式。
题目给出了成人票和儿童票的价格,以及购买的票数,我们需要找出总花费的表达式,
总花费由两部分组成:成人票的总价和儿童票的总价,
成人票的总价是 $30 × m$ 元(单价乘以数量),
儿童票的总价是 $15 × n$ 元(单价乘以数量),
因此,总花费就是成人票总价和儿童票总价的和,即 $30m + 15n$ 元,
这个表达式符合题目要求,也符合代数表达式的规范。
【答案】:
$(30m + 15n)$。
这个问题是一个代数表达式问题,需要我们将文字描述转化为数学表达式。
题目给出了成人票和儿童票的价格,以及购买的票数,我们需要找出总花费的表达式,
总花费由两部分组成:成人票的总价和儿童票的总价,
成人票的总价是 $30 × m$ 元(单价乘以数量),
儿童票的总价是 $15 × n$ 元(单价乘以数量),
因此,总花费就是成人票总价和儿童票总价的和,即 $30m + 15n$ 元,
这个表达式符合题目要求,也符合代数表达式的规范。
【答案】:
$(30m + 15n)$。
13. 木材加工厂将一批木料按如图所示的规律依次摆放,则第$n$个图中共有木料
$\frac{n(n+1)}{2}$
根。答案:解:第1个图:1根
第2个图:1+2=3根
第3个图:1+2+3=6根
第4个图:1+2+3+4=10根
...
第n个图:1+2+...+n=$\frac{n(n+1)}{2}$根
$\frac{n(n+1)}{2}$
第2个图:1+2=3根
第3个图:1+2+3=6根
第4个图:1+2+3+4=10根
...
第n个图:1+2+...+n=$\frac{n(n+1)}{2}$根
$\frac{n(n+1)}{2}$
14. 某县计划在一定时间内造林$m$公顷,原计划每月造林$a$公顷,实际每月多造林$b$公顷,则实际比原计划少用
$\frac{m}{a} - \frac{m}{a + b}$
月。答案:【解析】:
这个问题主要考察的是代数表达式的建立和代数运算。
原计划每月造林$a$公顷,所以原计划需要的时间是$\frac{m}{a}$个月。
实际上每月造林$a+b$公顷,所以实际需要的时间是$\frac{m}{a+b}$个月。
要求实际比原计划少用的月数,即求$\frac{m}{a} - \frac{m}{a+b}$。
【答案】:
$\frac{m}{a} - \frac{m}{a + b}$月。
这个问题主要考察的是代数表达式的建立和代数运算。
原计划每月造林$a$公顷,所以原计划需要的时间是$\frac{m}{a}$个月。
实际上每月造林$a+b$公顷,所以实际需要的时间是$\frac{m}{a+b}$个月。
要求实际比原计划少用的月数,即求$\frac{m}{a} - \frac{m}{a+b}$。
【答案】:
$\frac{m}{a} - \frac{m}{a + b}$月。
15. 如图,用同样的火柴棒按规律摆成边长分别为1,2,3,…,$(n - 1)$,$n$的正方形图案。
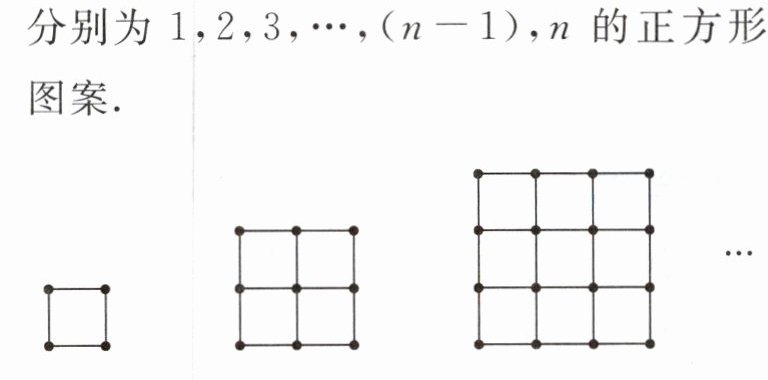
(1) 摆成边长为4的正方形图案时,需火柴棒的根数为______
(2) 边长为$n的正方形图案比边长为(n - 1)$的正方形图案多______
(3) 摆成边长为$n$的正方形图案时,需火柴棒的根数为______
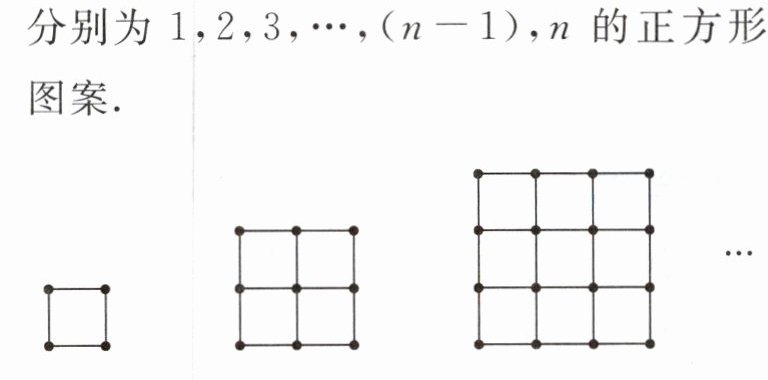
(1) 摆成边长为4的正方形图案时,需火柴棒的根数为______
40
;(2) 边长为$n的正方形图案比边长为(n - 1)$的正方形图案多______
$2n - 1$
个边长为1的小正方形;(3) 摆成边长为$n$的正方形图案时,需火柴棒的根数为______
$2n(n + 1)$
。答案:
(1) 40
(2) $2n - 1$
(3) $2n(n + 1)$
(1) 40
(2) $2n - 1$
(3) $2n(n + 1)$
16. 新趋势推导探究观察下列各式的规律:
①$1×3 - 2^{2} = 3 - 4 = -1$;
②$2×4 - 3^{2} = 8 - 9 = -1$;
③$3×5 - 4^{2} = 15 - 16 = -1$。
(1) 请按以上规律写出第4个算式:
(2) 用含字母$n(n≥1$,且为整数)的式子表示第$n$个算式:
①$1×3 - 2^{2} = 3 - 4 = -1$;
②$2×4 - 3^{2} = 8 - 9 = -1$;
③$3×5 - 4^{2} = 15 - 16 = -1$。
(1) 请按以上规律写出第4个算式:
$4 × 6 - 5^{2} = 24 - 25 = - 1$
;(2) 用含字母$n(n≥1$,且为整数)的式子表示第$n$个算式:
$n(n + 2) - (n + 1)^{2} = - 1$
。答案:【解析】:
(1)观察给出的算式,我们可以看到每个算式都遵循一个特定的模式:两个连续的整数相乘,然后减去这两个整数的平均数的平方。在第①个算式中,是$1×3 - 2^{2}$;在第②个算式中,是$2×4 - 3^{2}$;在第③个算式中,是$3×5 - 4^{2}$。根据这个模式,我们可以推断出第4个算式应该是$4×6 - 5^{2}$。
(2)对于用含字母$n(n\geq1$,且为整数)的式子表示第$n$个算式,我们可以观察到,在每个算式中,相乘的两个整数分别是$n$和$n+2$,而被减数则是这两个整数的平均数$n+1$的平方。因此,第$n$个算式可以表示为$n(n + 2) - (n + 1)^{2}$。
【答案】:
(1)$4 × 6 - 5^{2} = 24 - 25 = - 1$
(2)$n(n + 2) - (n + 1)^{2} = - 1$
(1)观察给出的算式,我们可以看到每个算式都遵循一个特定的模式:两个连续的整数相乘,然后减去这两个整数的平均数的平方。在第①个算式中,是$1×3 - 2^{2}$;在第②个算式中,是$2×4 - 3^{2}$;在第③个算式中,是$3×5 - 4^{2}$。根据这个模式,我们可以推断出第4个算式应该是$4×6 - 5^{2}$。
(2)对于用含字母$n(n\geq1$,且为整数)的式子表示第$n$个算式,我们可以观察到,在每个算式中,相乘的两个整数分别是$n$和$n+2$,而被减数则是这两个整数的平均数$n+1$的平方。因此,第$n$个算式可以表示为$n(n + 2) - (n + 1)^{2}$。
【答案】:
(1)$4 × 6 - 5^{2} = 24 - 25 = - 1$
(2)$n(n + 2) - (n + 1)^{2} = - 1$
17. 大学生康康自主创业,在风景秀丽的某景区湖边开了间咖啡馆。咖啡馆内每一张正方形桌子可坐4人,按照如图所示的方式将桌子拼在一起。试解答下列问题:
(1) 2张桌子拼在一起可以坐几人?3张桌子拼在一起可以坐几人?$n$张桌子拼在一起可以坐几人?
(2) 咖啡馆里共有60张这样的正方形桌子。若按(1)中方式每4张拼成一张大桌子,则60张桌子共可坐多少人?
(3) 在(2)中,若每4张桌子拼成一张大正方形桌子,则共可坐多少人?
(4) 对于咖啡馆,以上哪种拼桌子的方式可以使坐的人更多?
]

(1) 2张桌子拼在一起可以坐几人?3张桌子拼在一起可以坐几人?$n$张桌子拼在一起可以坐几人?
(2) 咖啡馆里共有60张这样的正方形桌子。若按(1)中方式每4张拼成一张大桌子,则60张桌子共可坐多少人?
(3) 在(2)中,若每4张桌子拼成一张大正方形桌子,则共可坐多少人?
(4) 对于咖啡馆,以上哪种拼桌子的方式可以使坐的人更多?
]

答案:【解析】:
本题主要考查了字母表示数以及通过规律计算总人数。
(1)对于2张桌子拼在一起,除了第一张桌子的一条边(2人)和最后一张桌子的一条边(2人)各自独立外,中间的桌子每张都贡献了两条边(各2人),但每两张桌子拼接时,会减少2个座位(因为拼接处两个桌子共用一边)。
所以2张桌子拼在一起时,人数为$4+2×(2-1)×2- 2×(2-1)=6$(人)(但此处直接观察可知为6人,因为只拼了一次,减少了2个座位)。
3张桌子拼在一起时,人数为$4+2×(3-1)×2- 2×(3-1)=8$(人)。
对于n张桌子拼在一起,人数为$4+2×(n-1)×2- 2×(n-1)=2n+2$(人)(因为每多拼一张桌子,就多出2个座位,但同时每拼一张就减少2个座位中的1个与上一张桌子共用,所以实际增加2个座位,但第一张和最后一张桌子各自独立贡献2个座位,故需加4再减去多减的$2×(n-1)$中的n-1个2)。但更直观的理解是,每张桌子本身4人,每拼一张减少2人,所以为$4n-2×(n-1)=2n+2$。
(2)每4张拼成一张大桌子,则每张大桌子可坐$2×4+2=10$(人)。
所以60张桌子可以拼成15张大桌子,共可坐$15×10=150$(人)。
(3)若每4张桌子拼成一张大正方形桌子,则每张大桌子可坐8人(通过观察或计算可得,四张桌子拼成一个大正方形,每个边各坐2人,但四个角各多算了一次,所以为$4×2+4-4=8$人)。
所以60张桌子可以拼成15张大正方形桌子,共可坐$15×8=120$(人)。
(4)比较(2)和(3)的结果,150人>120人,所以按(2)中方式拼桌子可以使坐的人更多。
【答案】:
(1)2张桌子拼在一起可以坐6人,3张桌子拼在一起可以坐8人,n张桌子拼在一起可以坐$(2n+2)$人;
(2)60张桌子共可坐150人;
(3)共可坐120人;
(4)按(2)中方式拼桌子可以使坐的人更多。
本题主要考查了字母表示数以及通过规律计算总人数。
(1)对于2张桌子拼在一起,除了第一张桌子的一条边(2人)和最后一张桌子的一条边(2人)各自独立外,中间的桌子每张都贡献了两条边(各2人),但每两张桌子拼接时,会减少2个座位(因为拼接处两个桌子共用一边)。
所以2张桌子拼在一起时,人数为$4+2×(2-1)×2- 2×(2-1)=6$(人)(但此处直接观察可知为6人,因为只拼了一次,减少了2个座位)。
3张桌子拼在一起时,人数为$4+2×(3-1)×2- 2×(3-1)=8$(人)。
对于n张桌子拼在一起,人数为$4+2×(n-1)×2- 2×(n-1)=2n+2$(人)(因为每多拼一张桌子,就多出2个座位,但同时每拼一张就减少2个座位中的1个与上一张桌子共用,所以实际增加2个座位,但第一张和最后一张桌子各自独立贡献2个座位,故需加4再减去多减的$2×(n-1)$中的n-1个2)。但更直观的理解是,每张桌子本身4人,每拼一张减少2人,所以为$4n-2×(n-1)=2n+2$。
(2)每4张拼成一张大桌子,则每张大桌子可坐$2×4+2=10$(人)。
所以60张桌子可以拼成15张大桌子,共可坐$15×10=150$(人)。
(3)若每4张桌子拼成一张大正方形桌子,则每张大桌子可坐8人(通过观察或计算可得,四张桌子拼成一个大正方形,每个边各坐2人,但四个角各多算了一次,所以为$4×2+4-4=8$人)。
所以60张桌子可以拼成15张大正方形桌子,共可坐$15×8=120$(人)。
(4)比较(2)和(3)的结果,150人>120人,所以按(2)中方式拼桌子可以使坐的人更多。
【答案】:
(1)2张桌子拼在一起可以坐6人,3张桌子拼在一起可以坐8人,n张桌子拼在一起可以坐$(2n+2)$人;
(2)60张桌子共可坐150人;
(3)共可坐120人;
(4)按(2)中方式拼桌子可以使坐的人更多。