1. 下列说法正确的是 (
A.单项式3的次数是1
B.$ x+\frac{a}{x}+1 $不是多项式
C.$ x^{3}-2x^{2}y^{2}+3y^{2} $是三次三项式
D.单项式$ \frac{3}{2}\pi r^{2} 的系数是 \frac{3}{2} $
B
)A.单项式3的次数是1
B.$ x+\frac{a}{x}+1 $不是多项式
C.$ x^{3}-2x^{2}y^{2}+3y^{2} $是三次三项式
D.单项式$ \frac{3}{2}\pi r^{2} 的系数是 \frac{3}{2} $
答案:【解析】:
本题考察的是对整式相关概念的理解。
A选项:单项式的次数是指其所有字母的指数之和。而数字3没有任何字母部分,因此它的次数是0,不是1。所以A选项错误。
B选项:多项式是由常数、变量、加法、减法、乘法和自然数次幂运算构成的代数表达式。而表达式$x+\frac{a}{x}+1$中,因为含有$\frac{a}{x}$这一项,它不是多项式,而是一个分式。所以B选项正确。
C选项:对于$x^{3}-2x^{2}y^{2}+3y^{2}$,我们需要观察它的最高次项来判断它的次数。最高次项是$-2x^{2}y^{2}$,它的次数是$x$的2次和$y$的2次之和,即4次。所以,它不是三次三项式,而是四次三项式。C选项错误。
D选项:单项式的系数是它前面的数字部分。对于单项式$\frac{3}{2}\pi r^{2}$,它的系数是$\frac{3}{2}\pi$,而不是$\frac{3}{2}$。所以D选项错误。
综上所述,只有B选项是正确的。
【答案】:
B
本题考察的是对整式相关概念的理解。
A选项:单项式的次数是指其所有字母的指数之和。而数字3没有任何字母部分,因此它的次数是0,不是1。所以A选项错误。
B选项:多项式是由常数、变量、加法、减法、乘法和自然数次幂运算构成的代数表达式。而表达式$x+\frac{a}{x}+1$中,因为含有$\frac{a}{x}$这一项,它不是多项式,而是一个分式。所以B选项正确。
C选项:对于$x^{3}-2x^{2}y^{2}+3y^{2}$,我们需要观察它的最高次项来判断它的次数。最高次项是$-2x^{2}y^{2}$,它的次数是$x$的2次和$y$的2次之和,即4次。所以,它不是三次三项式,而是四次三项式。C选项错误。
D选项:单项式的系数是它前面的数字部分。对于单项式$\frac{3}{2}\pi r^{2}$,它的系数是$\frac{3}{2}\pi$,而不是$\frac{3}{2}$。所以D选项错误。
综上所述,只有B选项是正确的。
【答案】:
B
2. 代数式$ ab,\frac{x - y}{3},\frac{3}{x},-xy^{2},0.1,\frac{3}{\pi},x^{2}+2xy + y^{2} $中,单项式有 (
A.5个
B.4个
C.3个
D.2个
B
)A.5个
B.4个
C.3个
D.2个
答案:【解析】:
本题主要考查整式的概念,特别是单项式的识别。
单项式是只含有一个项的代数式,即它只包含一个实数与若干个字母的乘积,或者仅包含一个实数(当没有字母时)。
需要逐一检查给定的代数式,判断它们是否满足单项式的定义:
$ab$:是单项式,因为它是两个字母的乘积。
$\frac{x - y}{3}$:不是单项式,因为它包含两个项$x$和$-y$。
$\frac{3}{x}$:不是单项式,因为分母含有字母。
$-xy^{2}$:是单项式,因为它是数字与字母的乘积。
$0.1$:是单项式,因为它是一个实数。
$\frac{3}{\pi}$:是单项式,因为$\pi$是一个常数,所以这也是一个实数与常数的商,可看作实数。
$x^{2} + 2xy + y^{2}$:不是单项式,因为它包含三个项。
统计单项式的个数,得到$ab, -xy^{2}, 0.1, \frac{3}{\pi}$,共有4个单项式。
【答案】:B.4个。
本题主要考查整式的概念,特别是单项式的识别。
单项式是只含有一个项的代数式,即它只包含一个实数与若干个字母的乘积,或者仅包含一个实数(当没有字母时)。
需要逐一检查给定的代数式,判断它们是否满足单项式的定义:
$ab$:是单项式,因为它是两个字母的乘积。
$\frac{x - y}{3}$:不是单项式,因为它包含两个项$x$和$-y$。
$\frac{3}{x}$:不是单项式,因为分母含有字母。
$-xy^{2}$:是单项式,因为它是数字与字母的乘积。
$0.1$:是单项式,因为它是一个实数。
$\frac{3}{\pi}$:是单项式,因为$\pi$是一个常数,所以这也是一个实数与常数的商,可看作实数。
$x^{2} + 2xy + y^{2}$:不是单项式,因为它包含三个项。
统计单项式的个数,得到$ab, -xy^{2}, 0.1, \frac{3}{\pi}$,共有4个单项式。
【答案】:B.4个。
3. (教材P85练习2变式)(2024·山东泰安)单项式$ -3ab^{2} $的次数为
3
.答案:【解析】:
本题考查的是单项式的次数。单项式的次数是指单项式中所有字母的指数之和。对于单项式 $-3ab^{2}$,其中 $a$ 的指数为 $1$,$b$ 的指数为 $2$。因此,该单项式的次数为 $1+2=3$。
【答案】:
3
本题考查的是单项式的次数。单项式的次数是指单项式中所有字母的指数之和。对于单项式 $-3ab^{2}$,其中 $a$ 的指数为 $1$,$b$ 的指数为 $2$。因此,该单项式的次数为 $1+2=3$。
【答案】:
3
4. 若多项式$ xy^{|m - n|}+(n - 2)x^{2}y^{2}+1 $是关于x,y的三次多项式,则$ mn = $
8或0
.答案:【解析】:
首先,我们分析多项式的次数。多项式的次数是由它的各项中次数最高的那一项决定的。
对于多项式中的第一项 $xy^{|m - n|}$,它的次数是 $1 + |m - n|$。
对于多项式中的第二项 $(n - 2)x^{2}y^{2}$,它的次数是 $2 + 2 = 4$。
由于这是一个关于x, y的三次多项式,所以最高次数的项必须是三次的。
因此,我们得到以下方程组:
1. $1 + |m - n| = 3$,以确保第一项是三次的。
2. $n - 2 = 0$,以确保第二项消失(因为三次多项式中不能有四次项)。
从第二个方程,我们得到 $n = 2$。
将 $n = 2$ 代入第一个方程,我们得到 $|m - 2| = 2$,
解这个方程,我们得到 $m = 4$ 或 $m = 0$。
所以,我们得到两组解:$m = 4, n = 2$ 或 $m = 0, n = 2$。
对于第一组解,$mn = 4 × 2 = 8$。
对于第二组解,$mn = 0 × 2 = 0$。
【答案】:
$mn = 8$ 或 $mn = 0$。
首先,我们分析多项式的次数。多项式的次数是由它的各项中次数最高的那一项决定的。
对于多项式中的第一项 $xy^{|m - n|}$,它的次数是 $1 + |m - n|$。
对于多项式中的第二项 $(n - 2)x^{2}y^{2}$,它的次数是 $2 + 2 = 4$。
由于这是一个关于x, y的三次多项式,所以最高次数的项必须是三次的。
因此,我们得到以下方程组:
1. $1 + |m - n| = 3$,以确保第一项是三次的。
2. $n - 2 = 0$,以确保第二项消失(因为三次多项式中不能有四次项)。
从第二个方程,我们得到 $n = 2$。
将 $n = 2$ 代入第一个方程,我们得到 $|m - 2| = 2$,
解这个方程,我们得到 $m = 4$ 或 $m = 0$。
所以,我们得到两组解:$m = 4, n = 2$ 或 $m = 0, n = 2$。
对于第一组解,$mn = 4 × 2 = 8$。
对于第二组解,$mn = 0 × 2 = 0$。
【答案】:
$mn = 8$ 或 $mn = 0$。
5. 若$ (m + n)x^{2}y^{n + 1} $是关于x,y的五次单项式且系数为6,求m,n的值.
答案:【解析】:
本题主要考查单项式的系数和次数的概念。
单项式的系数是单项式前面的数字部分,而单项式的次数是所有字母的指数之和。
根据题意,单项式$(m + n)x^{2}y^{n + 1}$是关于x,y的五次单项式且系数为6。
首先,考虑单项式的系数,我们有:
$m + n = 6$
这是因为单项式的系数是单项式前面的数字部分,即$m+n$。
其次,考虑单项式的次数,我们有:
$2 + (n + 1) = 5$
这是因为单项式的次数是所有字母的指数之和,即$x$的指数2加上$y$的指数$n+1$。
解这个方程组,我们得到:
$m + n = 6$
$2 + n + 1 = 5$
从第二个方程,我们可以解出:
$n = 2$
将$n = 2$代入第一个方程,我们得到:
$m = 4$
所以,$m = 4$,$n = 2$。
【答案】:
$m = 4$,$n = 2$。
本题主要考查单项式的系数和次数的概念。
单项式的系数是单项式前面的数字部分,而单项式的次数是所有字母的指数之和。
根据题意,单项式$(m + n)x^{2}y^{n + 1}$是关于x,y的五次单项式且系数为6。
首先,考虑单项式的系数,我们有:
$m + n = 6$
这是因为单项式的系数是单项式前面的数字部分,即$m+n$。
其次,考虑单项式的次数,我们有:
$2 + (n + 1) = 5$
这是因为单项式的次数是所有字母的指数之和,即$x$的指数2加上$y$的指数$n+1$。
解这个方程组,我们得到:
$m + n = 6$
$2 + n + 1 = 5$
从第二个方程,我们可以解出:
$n = 2$
将$n = 2$代入第一个方程,我们得到:
$m = 4$
所以,$m = 4$,$n = 2$。
【答案】:
$m = 4$,$n = 2$。
6. 下列各式中,不是单项式的为 (
A.3
B.a
C.$ \frac{b}{a} $
D.$ \frac{1}{2}x^{2}y $
C
)A.3
B.a
C.$ \frac{b}{a} $
D.$ \frac{1}{2}x^{2}y $
答案:【解析】:
本题主要考察单项式的定义。单项式是只含有一个项的代数式,即它是一个数与字母的积,或者单独的一个数或一个字母。
A. $3$ 是一个单独的数,所以是单项式。
B. $a$ 是一个单独的字母,所以是单项式。
C. $\frac{b}{a}$ 由于分母含有字母,因此它不是单项式,而是分式。
D. $\frac{1}{2}x^{2}y$ 是数与字母的积,所以是单项式。
根据以上分析,只有选项C不是单项式。
【答案】:
C
本题主要考察单项式的定义。单项式是只含有一个项的代数式,即它是一个数与字母的积,或者单独的一个数或一个字母。
A. $3$ 是一个单独的数,所以是单项式。
B. $a$ 是一个单独的字母,所以是单项式。
C. $\frac{b}{a}$ 由于分母含有字母,因此它不是单项式,而是分式。
D. $\frac{1}{2}x^{2}y$ 是数与字母的积,所以是单项式。
根据以上分析,只有选项C不是单项式。
【答案】:
C
7. 若多项式$ 4xy^{|k|}-\frac{1}{3}(k - 3)x^{2}+\frac{3}{5}y^{3}+1 $(k为常数)是四次四项式,则k的值是 (
A.$ \pm 3 $
B.3
C.-3
D.$ \pm 4 $
C
)A.$ \pm 3 $
B.3
C.-3
D.$ \pm 4 $
答案:【解析】:
首先,我们观察多项式$4xy^{|k|}-\frac{1}{3}(k - 3)x^{2}+\frac{3}{5}y^{3}+1$。
要使这个多项式是四次四项式,我们需要确定最高次项的次数为4。
观察多项式中的各项,最高次项是$4xy^{|k|}$,它的次数是$1+|k|$。
因此,我们有$1+|k|=4$。
解这个方程,我们得到$|k|=3$,即$k=\pm3$。
但是,我们还要注意到多项式中的第二项$-\frac{1}{3}(k - 3)x^{2}$。
如果$k=3$,那么第二项就会变为0,这样多项式就变成了三次三项式,与题目要求的四次四项式不符。
因此,我们排除$k=3$,只保留$k=-3$。
所以,$k$的值是$-3$。
【答案】:
C. $-3$。
首先,我们观察多项式$4xy^{|k|}-\frac{1}{3}(k - 3)x^{2}+\frac{3}{5}y^{3}+1$。
要使这个多项式是四次四项式,我们需要确定最高次项的次数为4。
观察多项式中的各项,最高次项是$4xy^{|k|}$,它的次数是$1+|k|$。
因此,我们有$1+|k|=4$。
解这个方程,我们得到$|k|=3$,即$k=\pm3$。
但是,我们还要注意到多项式中的第二项$-\frac{1}{3}(k - 3)x^{2}$。
如果$k=3$,那么第二项就会变为0,这样多项式就变成了三次三项式,与题目要求的四次四项式不符。
因此,我们排除$k=3$,只保留$k=-3$。
所以,$k$的值是$-3$。
【答案】:
C. $-3$。
8. 新趋势开放探究已知一个整式具备以下三个条件:①它是关于字母x的二次三项式;②各项系数的和等于10;③它的二次项系数和常数项都比-2小.请写出一个满足这些条件的整式:
-3x² + 17x - 4
.答案:解:设该整式为$ax^2 + bx + c$。
因为它是关于字母$x$的二次三项式,所以$a\neq0$,$b\neq0$,$c\neq0$。
二次项系数$a$和常数项$c$都比$-2$小,取$a=-3$,$c=-4$。
各项系数的和等于$10$,即$a + b + c = 10$,将$a=-3$,$c=-4$代入得:$-3 + b + (-4) = 10$,解得$b = 17$。
所以满足条件的整式可以是$-3x^2 + 17x - 4$。
$-3x^2 + 17x - 4$
因为它是关于字母$x$的二次三项式,所以$a\neq0$,$b\neq0$,$c\neq0$。
二次项系数$a$和常数项$c$都比$-2$小,取$a=-3$,$c=-4$。
各项系数的和等于$10$,即$a + b + c = 10$,将$a=-3$,$c=-4$代入得:$-3 + b + (-4) = 10$,解得$b = 17$。
所以满足条件的整式可以是$-3x^2 + 17x - 4$。
$-3x^2 + 17x - 4$
9. (2025·江苏无锡期末)观察下列等式:$ 1 = 1^{2}-0^{2},3 = 2^{2}-1^{2},5 = 3^{2}-2^{2},… $,按此规律,第n个等式为
$ 2n - 1 = n^{2} - (n - 1)^{2}$
.答案:【解析】:
这个问题要求我们观察给出的等式系列,找出其中的规律,并给出第n个等式的形式。通过观察,我们发现等式右侧是两个平方数的差,且这两个平方数的底数相差1。更具体地说,对于第n个等式,右侧可以表示为$n^2 - (n-1)^2$。
首先,我们验证给出的等式:
1. 当$n=1$时,$ 1 = 1^{2}-0^{2}$,
2. 当$n=2$时,$ 3 = 2^{2}-1^{2}$,
3. 当$n=3$时,$ 5 = 3^{2}-2^{2}$,
...
这样,我们可以归纳出第n个等式的一般形式为:$ 2n - 1 = n^{2} - (n-1)^{2}$。
为了验证这一点,我们可以展开右侧的表达式:
$n^{2} - (n-1)^{2} = n^{2} - (n^2 - 2n + 1) = 2n - 1$,
这与等式左侧给出的数列(1, 3, 5, ...)相匹配,该数列是一个等差数列,首项为1,公差为2,因此第n项可以表示为$2n-1$。
【答案】:
第n个等式为$ 2n - 1 = n^{2} - (n - 1)^{2}$。
这个问题要求我们观察给出的等式系列,找出其中的规律,并给出第n个等式的形式。通过观察,我们发现等式右侧是两个平方数的差,且这两个平方数的底数相差1。更具体地说,对于第n个等式,右侧可以表示为$n^2 - (n-1)^2$。
首先,我们验证给出的等式:
1. 当$n=1$时,$ 1 = 1^{2}-0^{2}$,
2. 当$n=2$时,$ 3 = 2^{2}-1^{2}$,
3. 当$n=3$时,$ 5 = 3^{2}-2^{2}$,
...
这样,我们可以归纳出第n个等式的一般形式为:$ 2n - 1 = n^{2} - (n-1)^{2}$。
为了验证这一点,我们可以展开右侧的表达式:
$n^{2} - (n-1)^{2} = n^{2} - (n^2 - 2n + 1) = 2n - 1$,
这与等式左侧给出的数列(1, 3, 5, ...)相匹配,该数列是一个等差数列,首项为1,公差为2,因此第n项可以表示为$2n-1$。
【答案】:
第n个等式为$ 2n - 1 = n^{2} - (n - 1)^{2}$。
10. 新素养几何直观用代数式表示下列各图形中阴影部分的面积.
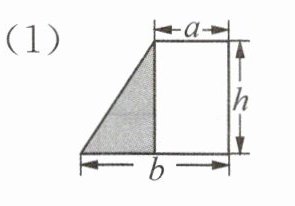



答案:(1)解:由图可知,梯形的下底为$b$,上底为$a$,高为$h$,阴影部分为三角形,底为$(b - a)$,高为$h$。
三角形面积公式为$\frac{1}{2}×底×高$,所以阴影部分面积为$\frac{1}{2}(b - a)h$。
(2)解:由图可知,长方形的长为$(a + b)$,宽为$a$,左边空白部分为半径为$a$的$\frac{1}{4}$圆,右边空白部分为半径为$b$的$\frac{1}{4}$圆。
长方形面积为$(a + b)a$,$\frac{1}{4}$圆面积公式为$\frac{1}{4}\pi r^2$,所以两个空白部分面积和为$\frac{1}{4}\pi a^2+\frac{1}{4}\pi b^2$。
阴影部分面积 = 长方形面积 - 空白部分面积,即$a(a + b)-\left(\frac{1}{4}\pi a^2+\frac{1}{4}\pi b^2\right)=a^2 + ab-\frac{1}{4}\pi a^2-\frac{1}{4}\pi b^2$。
三角形面积公式为$\frac{1}{2}×底×高$,所以阴影部分面积为$\frac{1}{2}(b - a)h$。
(2)解:由图可知,长方形的长为$(a + b)$,宽为$a$,左边空白部分为半径为$a$的$\frac{1}{4}$圆,右边空白部分为半径为$b$的$\frac{1}{4}$圆。
长方形面积为$(a + b)a$,$\frac{1}{4}$圆面积公式为$\frac{1}{4}\pi r^2$,所以两个空白部分面积和为$\frac{1}{4}\pi a^2+\frac{1}{4}\pi b^2$。
阴影部分面积 = 长方形面积 - 空白部分面积,即$a(a + b)-\left(\frac{1}{4}\pi a^2+\frac{1}{4}\pi b^2\right)=a^2 + ab-\frac{1}{4}\pi a^2-\frac{1}{4}\pi b^2$。
11. 按某种标准把多项式进行分类时,$ 3x^{3}-4 和 a^{2}b + ab^{2}+1 $属于同一类,则下列多项式中,也属于此类的是 (
A.$ abc - 1 $
B.$ x^{2}-2 $
C.$ 3x^{2}+2xy^{4} $
D.$ m^{2}+2mn + n^{2} $
A
)A.$ abc - 1 $
B.$ x^{2}-2 $
C.$ 3x^{2}+2xy^{4} $
D.$ m^{2}+2mn + n^{2} $
答案:解:多项式$3x^{3}-4$是三次二项式,多项式$a^{2}b + ab^{2}+1$是三次三项式,它们均为三次多项式。
A.$abc - 1$是三次二项式,属于三次多项式;
B.$x^{2}-2$是二次二项式;
C.$3x^{2}+2xy^{4}$是五次二项式;
D.$m^{2}+2mn + n^{2}$是二次三项式。
故选A。
A.$abc - 1$是三次二项式,属于三次多项式;
B.$x^{2}-2$是二次二项式;
C.$3x^{2}+2xy^{4}$是五次二项式;
D.$m^{2}+2mn + n^{2}$是二次三项式。
故选A。
12. 已知m,n是正整数,a,b,c均不为0.若多项式$ a^{m + 1}b^{2}c-\frac{1}{7}ab^{n + 1}c^{2}+\frac{1}{12}a^{m + 3}b^{n}c $是八次三项式,求m,n的值.
答案:解:多项式各项次数分别为:
第一项:$m + 1 + 2 + 1 = m + 4$
第二项:$1 + n + 1 + 2 = n + 4$
第三项:$m + 3 + n + 1 = m + n + 4$
因为多项式是八次三项式,所以最高次项次数为8,且各项次数不超过8,m,n为正整数。
情况一:$m + 4 = 8$,则$m = 4$。
此时最高次项可能为第三项:$m + n + 4 = 8 + n$,若$8 + n > 8$,则与最高次为8矛盾,所以$n + 4 \leq 8$且$m + n + 4 \leq 8$。
$m = 4$代入$m + n + 4 \leq 8$,得$n \leq 0$,与n是正整数矛盾,舍去。
情况二:$n + 4 = 8$,则$n = 4$。
此时最高次项可能为第三项:$m + n + 4 = m + 8$,若$m + 8 > 8$,则与最高次为8矛盾,所以$m + 4 \leq 8$且$m + n + 4 \leq 8$。
$n = 4$代入$m + n + 4 \leq 8$,得$m \leq 0$,与m是正整数矛盾,舍去。
情况三:$m + n + 4 = 8$,即$m + n = 4$。
因为m,n是正整数,所以可能的解为:
$\begin{cases}m=1\\n=3\end{cases}$,此时第一项次数$1 + 4 = 5$,第二项次数$3 + 4 = 7$,均小于8,符合题意。
$\begin{cases}m=2\\n=2\end{cases}$,第一项次数$2 + 4 = 6$,第二项次数$2 + 4 = 6$,均小于8,符合题意。
$\begin{cases}m=3\\n=1\end{cases}$,第一项次数$3 + 4 = 7$,第二项次数$1 + 4 = 5$,均小于8,符合题意。
综上,m,n的值为$\begin{cases}m=1\\n=3\end{cases}$或$\begin{cases}m=2\\n=2\end{cases}$或$\begin{cases}m=3\\n=1\end{cases}$。
第一项:$m + 1 + 2 + 1 = m + 4$
第二项:$1 + n + 1 + 2 = n + 4$
第三项:$m + 3 + n + 1 = m + n + 4$
因为多项式是八次三项式,所以最高次项次数为8,且各项次数不超过8,m,n为正整数。
情况一:$m + 4 = 8$,则$m = 4$。
此时最高次项可能为第三项:$m + n + 4 = 8 + n$,若$8 + n > 8$,则与最高次为8矛盾,所以$n + 4 \leq 8$且$m + n + 4 \leq 8$。
$m = 4$代入$m + n + 4 \leq 8$,得$n \leq 0$,与n是正整数矛盾,舍去。
情况二:$n + 4 = 8$,则$n = 4$。
此时最高次项可能为第三项:$m + n + 4 = m + 8$,若$m + 8 > 8$,则与最高次为8矛盾,所以$m + 4 \leq 8$且$m + n + 4 \leq 8$。
$n = 4$代入$m + n + 4 \leq 8$,得$m \leq 0$,与m是正整数矛盾,舍去。
情况三:$m + n + 4 = 8$,即$m + n = 4$。
因为m,n是正整数,所以可能的解为:
$\begin{cases}m=1\\n=3\end{cases}$,此时第一项次数$1 + 4 = 5$,第二项次数$3 + 4 = 7$,均小于8,符合题意。
$\begin{cases}m=2\\n=2\end{cases}$,第一项次数$2 + 4 = 6$,第二项次数$2 + 4 = 6$,均小于8,符合题意。
$\begin{cases}m=3\\n=1\end{cases}$,第一项次数$3 + 4 = 7$,第二项次数$1 + 4 = 5$,均小于8,符合题意。
综上,m,n的值为$\begin{cases}m=1\\n=3\end{cases}$或$\begin{cases}m=2\\n=2\end{cases}$或$\begin{cases}m=3\\n=1\end{cases}$。