1. 将代数式$2x^{2}-3(2x-1)$中的括号去掉,结果正确的是 (
A.$2x^{2}-2x+1$
B.$2x^{2}-6x+3$
C.$2x^{2}-6x-3$
D.$2x^{2}+6x+3$
B
)A.$2x^{2}-2x+1$
B.$2x^{2}-6x+3$
C.$2x^{2}-6x-3$
D.$2x^{2}+6x+3$
答案:【解析】:
本题主要考察代数式中去括号的规则。
根据去括号法则,我们需要将括号内的每一项与括号外的数相乘,即:
$2x^{2} - 3(2x - 1) = 2x^{2} - 3 × 2x + 3 × 1$
$= 2x^{2} - 6x + 3$
与选项进行对比,可以看出正确答案是B。
【答案】:
B
本题主要考察代数式中去括号的规则。
根据去括号法则,我们需要将括号内的每一项与括号外的数相乘,即:
$2x^{2} - 3(2x - 1) = 2x^{2} - 3 × 2x + 3 × 1$
$= 2x^{2} - 6x + 3$
与选项进行对比,可以看出正确答案是B。
【答案】:
B
2. 下列去括号正确的是 (
A.$x-(-2x^{2}+x^{3})= x+2x^{2}-x^{3}$
B.$-(a+b)= -a+b$
C.$2(a+b)= 2a-2b$
D.$-x-(y-z)= -x-y-z$
A
)A.$x-(-2x^{2}+x^{3})= x+2x^{2}-x^{3}$
B.$-(a+b)= -a+b$
C.$2(a+b)= 2a-2b$
D.$-x-(y-z)= -x-y-z$
答案:【解析】:
本题主要考查去括号的运算规则。
对于选项A:
$x-(-2x^{2}+x^{3})$
根据去括号的规则,当括号前是负号时,去掉括号,括号里的各项都要变号。所以,
$x-(-2x^{2}+x^{3}) = x + 2x^{2} - x^{3}$
与选项A给出的结果一致,所以A是正确的。
对于选项B:
$-(a+b)$
根据去括号的规则,当括号前是负号时,去掉括号,括号里的各项都要变号。所以,
$-(a+b) = -a - b$
与选项B给出的$-a+b$不一致,所以B是错误的。
对于选项C:
$2(a+b)$
根据去括号的规则,当括号前是数字时,用乘法分配律展开。所以,
$2(a+b) = 2a + 2b$
与选项C给出的$2a-2b$不一致,所以C是错误的。
对于选项D:
$-x-(y-z)$
根据去括号的规则,去掉括号得,
$-x-(y-z) = -x - y + z$
与选项D给出的$-x-y-z$不一致,所以D是错误的。
综上所述,只有选项A是正确的。
【答案】:
A
本题主要考查去括号的运算规则。
对于选项A:
$x-(-2x^{2}+x^{3})$
根据去括号的规则,当括号前是负号时,去掉括号,括号里的各项都要变号。所以,
$x-(-2x^{2}+x^{3}) = x + 2x^{2} - x^{3}$
与选项A给出的结果一致,所以A是正确的。
对于选项B:
$-(a+b)$
根据去括号的规则,当括号前是负号时,去掉括号,括号里的各项都要变号。所以,
$-(a+b) = -a - b$
与选项B给出的$-a+b$不一致,所以B是错误的。
对于选项C:
$2(a+b)$
根据去括号的规则,当括号前是数字时,用乘法分配律展开。所以,
$2(a+b) = 2a + 2b$
与选项C给出的$2a-2b$不一致,所以C是错误的。
对于选项D:
$-x-(y-z)$
根据去括号的规则,去掉括号得,
$-x-(y-z) = -x - y + z$
与选项D给出的$-x-y-z$不一致,所以D是错误的。
综上所述,只有选项A是正确的。
【答案】:
A
3. 在等式$1-a^{2}+2ab-b^{2}= 1-( )$中,括号内应填 (
A.$a^{2}-2ab+b^{2}$
B.$a^{2}-2ab-b^{2}$
C.$-a^{2}-2ab+b^{2}$
D.$-a^{2}+2ab-b^{2}$
A
)A.$a^{2}-2ab+b^{2}$
B.$a^{2}-2ab-b^{2}$
C.$-a^{2}-2ab+b^{2}$
D.$-a^{2}+2ab-b^{2}$
答案:【解析】:
本题主要考察去括号和代数式的变形。
首先,我们观察原等式 $1-a^{2}+2ab-b^{2}= 1-( )$,需要找到一个表达式填入括号,使得等式成立。
我们可以将等式左边的 $1-a^{2}+2ab-b^{2}$ 改写为 $1-(a^{2}-2ab+b^{2})$,这样括号内的表达式就是我们需要找的答案。
通过对比选项,我们发现 $a^{2}-2ab+b^{2}$ 对应选项 A。
【答案】:
A
本题主要考察去括号和代数式的变形。
首先,我们观察原等式 $1-a^{2}+2ab-b^{2}= 1-( )$,需要找到一个表达式填入括号,使得等式成立。
我们可以将等式左边的 $1-a^{2}+2ab-b^{2}$ 改写为 $1-(a^{2}-2ab+b^{2})$,这样括号内的表达式就是我们需要找的答案。
通过对比选项,我们发现 $a^{2}-2ab+b^{2}$ 对应选项 A。
【答案】:
A
4. 去括号:
(1)$a+(-b-c)= $
(2)$a-(-b-c)= $
(3)$-[-(a+b)]-[-(a-b)]= $
(1)$a+(-b-c)= $
$a - b - c$
;(2)$a-(-b-c)= $
$a + b + c$
;(3)$-[-(a+b)]-[-(a-b)]= $
$2a$
.答案:【解析】:
本题主要考察去括号的运算。
(1) 对于 $a+(-b-c)$,去括号后得到 $a - b - c$。
(2) 对于 $a-(-b-c)$,去括号后得到 $a + b + c$。
(3) 对于 $-[-(a+b)]-[-(a-b)]$,首先处理内层的括号,得到 $-(-a-b)-(-a+b)$,再去外层括号,得到 $a + b + a - b$。
【答案】:
(1) $a - b - c$
(2) $a + b + c$
(3) $2a$
本题主要考察去括号的运算。
(1) 对于 $a+(-b-c)$,去括号后得到 $a - b - c$。
(2) 对于 $a-(-b-c)$,去括号后得到 $a + b + c$。
(3) 对于 $-[-(a+b)]-[-(a-b)]$,首先处理内层的括号,得到 $-(-a-b)-(-a+b)$,再去外层括号,得到 $a + b + a - b$。
【答案】:
(1) $a - b - c$
(2) $a + b + c$
(3) $2a$
5. 计算:$2a^{2}-(a^{2}+2)= $
$a^{2}-2$
.答案:【解析】:
本题主要考查去括号和合并同类项的知识点。
首先,我们需要去掉括号,根据去括号的规则,括号前的负号会改变括号内每一项的符号,所以$2a^{2}-(a^{2}+2)$可以化简为$2a^{2}-a^{2}-2$。
然后,我们合并同类项,即将相同次数的项相加或相减,所以$2a^{2}-a^{2}-2$可以化简为$a^{2}-2$。
【答案】:
$a^{2}-2$
本题主要考查去括号和合并同类项的知识点。
首先,我们需要去掉括号,根据去括号的规则,括号前的负号会改变括号内每一项的符号,所以$2a^{2}-(a^{2}+2)$可以化简为$2a^{2}-a^{2}-2$。
然后,我们合并同类项,即将相同次数的项相加或相减,所以$2a^{2}-a^{2}-2$可以化简为$a^{2}-2$。
【答案】:
$a^{2}-2$
6. 当$1≤m<3$时,化简:$|m-1|-|m-3|= $
$2m - 4$
.答案:【解析】:
本题主要考查绝对值的性质以及去括号的方法。
首先,根据题目条件,$1 \leq m < 3$。
对于$|m-1|$,由于$m \geq 1$,则$m-1 \geq 0$,所以$|m-1| = m-1$。
对于$|m-3|$,由于$m < 3$,则$m-3 < 0$,所以$|m-3| = -(m-3) = 3-m$。
将以上两个结果代入原式,得到:
$|m-1| - |m-3| = (m-1) - (3-m)$,
去括号后得到:
$m - 1 - 3 + m = 2m - 4$,
【答案】:
$2m - 4$。
本题主要考查绝对值的性质以及去括号的方法。
首先,根据题目条件,$1 \leq m < 3$。
对于$|m-1|$,由于$m \geq 1$,则$m-1 \geq 0$,所以$|m-1| = m-1$。
对于$|m-3|$,由于$m < 3$,则$m-3 < 0$,所以$|m-3| = -(m-3) = 3-m$。
将以上两个结果代入原式,得到:
$|m-1| - |m-3| = (m-1) - (3-m)$,
去括号后得到:
$m - 1 - 3 + m = 2m - 4$,
【答案】:
$2m - 4$。
7. (教材 P92 练习 2 变式)化简:
(1)$2(2b-3a)+3(2a-3b);$
(2)$4a^{2}+2(3ab-2a^{2})-(7ab-1).$
(1)$2(2b-3a)+3(2a-3b);$
(2)$4a^{2}+2(3ab-2a^{2})-(7ab-1).$
答案:【解析】:
本题主要考查了去括号和合并同类项的知识点。
对于第一个表达式 $2(2b-3a)+3(2a-3b)$,首先需要去括号,然后合并同类项。
去括号:根据分配律,$2(2b-3a) = 4b - 6a$,$3(2a-3b) = 6a - 9b$。
合并同类项:将去括号后的各项进行合并,即 $4b - 6a + 6a - 9b = -5b$。
对于第二个表达式 $4a^{2}+2(3ab-2a^{2})-(7ab-1)$,同样需要去括号,然后合并同类项。
去括号:根据分配律,$2(3ab-2a^{2}) = 6ab - 4a^{2}$,$-(7ab-1) = -7ab + 1$。
合并同类项:将去括号后的各项进行合并,即 $4a^{2} + 6ab - 4a^{2} - 7ab + 1 = -ab + 1$。
【答案】:
(1) $-5b$
(2) $-ab + 1$
本题主要考查了去括号和合并同类项的知识点。
对于第一个表达式 $2(2b-3a)+3(2a-3b)$,首先需要去括号,然后合并同类项。
去括号:根据分配律,$2(2b-3a) = 4b - 6a$,$3(2a-3b) = 6a - 9b$。
合并同类项:将去括号后的各项进行合并,即 $4b - 6a + 6a - 9b = -5b$。
对于第二个表达式 $4a^{2}+2(3ab-2a^{2})-(7ab-1)$,同样需要去括号,然后合并同类项。
去括号:根据分配律,$2(3ab-2a^{2}) = 6ab - 4a^{2}$,$-(7ab-1) = -7ab + 1$。
合并同类项:将去括号后的各项进行合并,即 $4a^{2} + 6ab - 4a^{2} - 7ab + 1 = -ab + 1$。
【答案】:
(1) $-5b$
(2) $-ab + 1$
8. (2025·江苏盐城期末)已知代数式$A= 2x^{2}+ax-1,B= -x^{2}-1.$
(1)求$3A+6B;$
(2)若$3A+6B$的值与x的取值无关,求a的值.
(1)求$3A+6B;$
(2)若$3A+6B$的值与x的取值无关,求a的值.
答案:【解析】:
(1) 主要考查代数式的加减运算,需要掌握去括号和合并同类项的方法。
首先,将A和B的表达式代入$3A+6B$中,然后去括号,最后合并同类项。
(2) 主要考查代数式的值与变量取值的关系,需要理解代数式与x无关的含义,即代数式化简后x的系数为0。
根据$3A+6B$化简后的结果,找到x的系数,并令其为0,解出a的值。
【答案】:
(1) 解:
代入A和B的表达式到$3A+6B$中,得到:
$3A+6B=3(2x^{2}+ax-1)+6(-x^{2}-1)$
$= 6x^{2} + 3ax - 3 - 6x^{2} - 6$
$= 3ax - 9$
(2) 解:
由于$3A+6B$的值与x的取值无关,所以x的系数必须为0,即:
$3a = 0$
解得:$a = 0$。
(1) 主要考查代数式的加减运算,需要掌握去括号和合并同类项的方法。
首先,将A和B的表达式代入$3A+6B$中,然后去括号,最后合并同类项。
(2) 主要考查代数式的值与变量取值的关系,需要理解代数式与x无关的含义,即代数式化简后x的系数为0。
根据$3A+6B$化简后的结果,找到x的系数,并令其为0,解出a的值。
【答案】:
(1) 解:
代入A和B的表达式到$3A+6B$中,得到:
$3A+6B=3(2x^{2}+ax-1)+6(-x^{2}-1)$
$= 6x^{2} + 3ax - 3 - 6x^{2} - 6$
$= 3ax - 9$
(2) 解:
由于$3A+6B$的值与x的取值无关,所以x的系数必须为0,即:
$3a = 0$
解得:$a = 0$。
9. 新素养 几何直观 已知有理数a,b在数轴上的位置如图所示,则化简$|a+b|-2|a-b|$的结果为 (
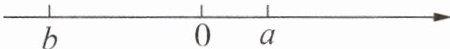
A.$-3a+b$
B.$-2a-b$
C.$2a+b$
D.$-a-b$
A
)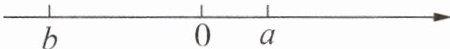
A.$-3a+b$
B.$-2a-b$
C.$2a+b$
D.$-a-b$
答案:【解析】:本题可根据有理数$a$、$b$在数轴上的位置判断$a + b$与$a - b$的正负性,再根据绝对值的性质去掉绝对值符号,最后进行化简。
步骤一:判断$a + b$与$a - b$的正负性
由数轴可知$b\lt0\lt a$,且$\vert b\vert\gt\vert a\vert$。
对于$a + b$:因为$b$是负数且绝对值较大,$a$是正数且绝对值较小,异号两数相加,取绝对值较大的符号,所以$a + b\lt0$。
对于$a - b$:因为$b\lt0$,那么$-b\gt0$,$a$是正数,两个正数相加结果为正,所以$a - b=a+(-b)\gt0$。
步骤二:根据绝对值的性质去掉绝对值符号
根据绝对值的性质:当$x\lt0$时,$\vert x\vert=-x$;当$x\gt0$时,$\vert x\vert=x$。
因为$a + b\lt0$,所以$\vert a + b\vert=-(a + b)=-a - b$。
因为$a - b\gt0$,所以$\vert a - b\vert=a - b$,则$2\vert a - b\vert = 2(a - b)=2a - 2b$。
步骤三:化简$\vert a + b\vert - 2\vert a - b\vert$
将$\vert a + b\vert=-a - b$,$2\vert a - b\vert = 2a - 2b$代入$\vert a + b\vert - 2\vert a - b\vert$可得:
$\vert a + b\vert - 2\vert a - b\vert=-a - b-(2a - 2b)$
去括号:$-a - b-(2a - 2b)=-a - b - 2a + 2b$
合并同类项:$-a - b - 2a + 2b=(-a - 2a)+(-b + 2b)=-3a + b$
【答案】:A
步骤一:判断$a + b$与$a - b$的正负性
由数轴可知$b\lt0\lt a$,且$\vert b\vert\gt\vert a\vert$。
对于$a + b$:因为$b$是负数且绝对值较大,$a$是正数且绝对值较小,异号两数相加,取绝对值较大的符号,所以$a + b\lt0$。
对于$a - b$:因为$b\lt0$,那么$-b\gt0$,$a$是正数,两个正数相加结果为正,所以$a - b=a+(-b)\gt0$。
步骤二:根据绝对值的性质去掉绝对值符号
根据绝对值的性质:当$x\lt0$时,$\vert x\vert=-x$;当$x\gt0$时,$\vert x\vert=x$。
因为$a + b\lt0$,所以$\vert a + b\vert=-(a + b)=-a - b$。
因为$a - b\gt0$,所以$\vert a - b\vert=a - b$,则$2\vert a - b\vert = 2(a - b)=2a - 2b$。
步骤三:化简$\vert a + b\vert - 2\vert a - b\vert$
将$\vert a + b\vert=-a - b$,$2\vert a - b\vert = 2a - 2b$代入$\vert a + b\vert - 2\vert a - b\vert$可得:
$\vert a + b\vert - 2\vert a - b\vert=-a - b-(2a - 2b)$
去括号:$-a - b-(2a - 2b)=-a - b - 2a + 2b$
合并同类项:$-a - b - 2a + 2b=(-a - 2a)+(-b + 2b)=-3a + b$
【答案】:A
10. 数学课上,老师讲了多项式去括号,放学后,小明回到家拿出课堂笔记,认真地复习老师讲的内容,他发现一道题:$(-x^{2}+3xy-\frac {1}{2}y^{2})-(-\frac {1}{2}x^{2}+4xy-\frac {3}{2}y^{2})= -\frac {1}{2}x^{2}$____$+y^{2}$,横线的地方被墨水弄污了,那么横线上应填的是 (
A.$-7xy$
B.$+7xy$
C.$-xy$
D.$+xy$
C
)A.$-7xy$
B.$+7xy$
C.$-xy$
D.$+xy$
答案:【解析】:
首先,我们需要去括号,并合并同类项。
原式可以写为:
$(-x^{2}+3xy-\frac {1}{2}y^{2})-(-\frac {1}{2}x^{2}+4xy-\frac {3}{2}y^{2})$
去括号后得到:
$-x^{2}+3xy-\frac {1}{2}y^{2}+\frac {1}{2}x^{2}-4xy+\frac {3}{2}y^{2}$
接着,我们合并同类项:
对于$x^{2}$的项:$-x^{2} + \frac{1}{2}x^{2} = -\frac{1}{2}x^{2}$
对于$y^{2}$的项:$-\frac{1}{2}y^{2} + \frac{3}{2}y^{2} = y^{2}$
对于$xy$的项:$3xy - 4xy = -xy$
所以,整理后的式子为:
$-\frac{1}{2}x^{2} - xy + y^{2}$
与题目中给出的式子对比,可以看出横线上应填的是$-xy$。
【答案】:C. $-xy$
首先,我们需要去括号,并合并同类项。
原式可以写为:
$(-x^{2}+3xy-\frac {1}{2}y^{2})-(-\frac {1}{2}x^{2}+4xy-\frac {3}{2}y^{2})$
去括号后得到:
$-x^{2}+3xy-\frac {1}{2}y^{2}+\frac {1}{2}x^{2}-4xy+\frac {3}{2}y^{2}$
接着,我们合并同类项:
对于$x^{2}$的项:$-x^{2} + \frac{1}{2}x^{2} = -\frac{1}{2}x^{2}$
对于$y^{2}$的项:$-\frac{1}{2}y^{2} + \frac{3}{2}y^{2} = y^{2}$
对于$xy$的项:$3xy - 4xy = -xy$
所以,整理后的式子为:
$-\frac{1}{2}x^{2} - xy + y^{2}$
与题目中给出的式子对比,可以看出横线上应填的是$-xy$。
【答案】:C. $-xy$
11. 已知多项式$x^{2}-kxy-3(x^{2}-12xy+x)$中不含xy项,则k的值为 (
A.-36
B.36
C.0
D.18
B
)A.-36
B.36
C.0
D.18
答案:【解析】:
本题主要考察多项式的合并同类项以及去括号的规则。
首先,我们需要将多项式$x^{2}-kxy-3(x^{2}-12xy+x)$进行去括号操作,得到:$x^{2}-kxy-3x^{2}+36xy-3x$。
然后,我们将同类项进行合并,得到:$-2x^{2}+(36-k)xy-3x$。
由于题目要求多项式中不含$xy$项,即$(36-k)xy$这一项需要为0,所以我们有:$36-k=0$。
解这个方程,我们得到:$k=36$。
【答案】:
B
本题主要考察多项式的合并同类项以及去括号的规则。
首先,我们需要将多项式$x^{2}-kxy-3(x^{2}-12xy+x)$进行去括号操作,得到:$x^{2}-kxy-3x^{2}+36xy-3x$。
然后,我们将同类项进行合并,得到:$-2x^{2}+(36-k)xy-3x$。
由于题目要求多项式中不含$xy$项,即$(36-k)xy$这一项需要为0,所以我们有:$36-k=0$。
解这个方程,我们得到:$k=36$。
【答案】:
B
12. (2024·四川德阳)若一个多项式加上$y^{2}+3xy-4$,结果是$3xy+2y^{2}-5$,则这个多项式为
$y^{2}-1$
.答案:【解析】:
本题考查了整式的加减运算。
根据题意,需要找到一个多项式,使其与$y^{2}+3xy-4$相加后,结果为$3xy+2y^{2}-5$。
设这个多项式为$P(x, y)$,则有:
$P(x, y) + (y^{2} + 3xy - 4) = 3xy + 2y^{2} - 5$,
为了求出$P(x, y)$,我们需要将$y^{2} + 3xy - 4$从等式的右边移至左边,即:
$P(x, y) = (3xy + 2y^{2} - 5) - (y^{2} + 3xy - 4)$,
去括号,合并同类项:
$P(x, y) = 3xy + 2y^{2} - 5 - y^{2} - 3xy + 4$,
$P(x, y) = (2y^{2} - y^{2}) + (3xy - 3xy) + (-5 + 4)$,
$P(x, y) = y^{2} - 1$。
【答案】:
$y^{2} - 1$。
本题考查了整式的加减运算。
根据题意,需要找到一个多项式,使其与$y^{2}+3xy-4$相加后,结果为$3xy+2y^{2}-5$。
设这个多项式为$P(x, y)$,则有:
$P(x, y) + (y^{2} + 3xy - 4) = 3xy + 2y^{2} - 5$,
为了求出$P(x, y)$,我们需要将$y^{2} + 3xy - 4$从等式的右边移至左边,即:
$P(x, y) = (3xy + 2y^{2} - 5) - (y^{2} + 3xy - 4)$,
去括号,合并同类项:
$P(x, y) = 3xy + 2y^{2} - 5 - y^{2} - 3xy + 4$,
$P(x, y) = (2y^{2} - y^{2}) + (3xy - 3xy) + (-5 + 4)$,
$P(x, y) = y^{2} - 1$。
【答案】:
$y^{2} - 1$。