1. (2024·山东威海)一批食品,标准质量为每袋 454 g. 现随机抽取 4 袋样品进行检测,把超过标准质量的克数用正数表示,不足标准质量的克数用负数表示,那么最接近标准质量的是 (
A.+7 g
B.-5 g
C.-3 g
D.10 g
C
)A.+7 g
B.-5 g
C.-3 g
D.10 g
答案:【解析】:
本题考查正数与负数在实际生活中的应用,特别是如何理解“最接近标准质量”这一表述。
“最接近标准质量”意味着与标准质量的差的绝对值最小。
分别计算四个选项与标准质量差的绝对值:
A. $|+7| = 7$
B. $|-5| = 5$
C. $|-3| = 3$
D. $|10| = 10$
比较这四个绝对值,发现$|-3| = 3$是最小的。
【答案】:
C
本题考查正数与负数在实际生活中的应用,特别是如何理解“最接近标准质量”这一表述。
“最接近标准质量”意味着与标准质量的差的绝对值最小。
分别计算四个选项与标准质量差的绝对值:
A. $|+7| = 7$
B. $|-5| = 5$
C. $|-3| = 3$
D. $|10| = 10$
比较这四个绝对值,发现$|-3| = 3$是最小的。
【答案】:
C
2. 新趋势 传统文化 (2023·湖南永州)我国古代数学名著《九章算术》中对正负数的概念注有“今两算得失相反,要令正负以名之”. 如:粮库把运进 30 t 粮食记为“+30”,则“-30”表示 (
A.运出 30 t 粮食
B.亏损 30 t 粮食
C.卖掉 30 t 粮食
D.吃掉 30 t 粮食
A
)A.运出 30 t 粮食
B.亏损 30 t 粮食
C.卖掉 30 t 粮食
D.吃掉 30 t 粮食
答案:【解析】:
这个问题考查的是对正负数在实际应用中的理解。在古代数学名著《九章算术》中,正负数被用来表示相反意义的量。题目中提到,粮库把运进30吨粮食记为“+30”,这是一个正数,表示粮食的增加。那么,相对应的,“-30”就应该表示粮食的减少,即运出30吨粮食。
【答案】:
A.运出 30 t 粮食
这个问题考查的是对正负数在实际应用中的理解。在古代数学名著《九章算术》中,正负数被用来表示相反意义的量。题目中提到,粮库把运进30吨粮食记为“+30”,这是一个正数,表示粮食的增加。那么,相对应的,“-30”就应该表示粮食的减少,即运出30吨粮食。
【答案】:
A.运出 30 t 粮食
3. 在校秋季运动会上,跳远比赛的晋级线为 4 m. 若小晨跳出了 4.25 m,记作+0.25 m,则小玲跳出了 3.85 m,记作
-0.15
m.答案:【解析】:
题目考查了正数与负数的实际应用,用正负数来表示实际数值与基准值(晋级线)之间的差异。题目中给出了小晨的跳远成绩与晋级线的差值作为正数(+0.25m),要求我们用同样的方式表示小玲的跳远成绩与晋级线的差值。
首先,确定晋级线为4m,小晨的跳远成绩为4.25m,与晋级线的差值为+0.25m。
然后,根据小玲的跳远成绩3.85m,计算与晋级线的差值:
$3.85m - 4m = -0.15m$。
【答案】:
$-0.15$
题目考查了正数与负数的实际应用,用正负数来表示实际数值与基准值(晋级线)之间的差异。题目中给出了小晨的跳远成绩与晋级线的差值作为正数(+0.25m),要求我们用同样的方式表示小玲的跳远成绩与晋级线的差值。
首先,确定晋级线为4m,小晨的跳远成绩为4.25m,与晋级线的差值为+0.25m。
然后,根据小玲的跳远成绩3.85m,计算与晋级线的差值:
$3.85m - 4m = -0.15m$。
【答案】:
$-0.15$
4. 用正负数表示气温的变化量,上升为正,下降为负. 登山队攀登一座山峰,每登高 1 km 气温的变化量为-6℃,则攀登 2 km 后,气温下降
12
℃.答案:【解析】:
题目考查了正负数在实际问题中的应用。
根据题意,每登高1km,气温的变化量为-6℃,即气温下降6℃。
因此,登高2km时,气温的总变化量为2次1km的变化量之和,即$2 × (-6)℃ = -12℃$。
但题目要求的是气温下降的度数,所以应取绝对值,即12℃。
不过由于题目已经明确是“下降”,且变化量为负,所以直接读出下降12℃即可。
【答案】:
12
题目考查了正负数在实际问题中的应用。
根据题意,每登高1km,气温的变化量为-6℃,即气温下降6℃。
因此,登高2km时,气温的总变化量为2次1km的变化量之和,即$2 × (-6)℃ = -12℃$。
但题目要求的是气温下降的度数,所以应取绝对值,即12℃。
不过由于题目已经明确是“下降”,且变化量为负,所以直接读出下降12℃即可。
【答案】:
12
5. 若 a 为不超过$ 1\frac{1}{4}$的正整数,b 为$\frac{1}{2}与 2\frac{1}{3}$之间的整数,则$\frac{a}{b}= $
$1或\frac{1}{2}$
.答案:【解析】:
题目考查正负数的认识,以及正负数的取值范围,需要分别求出a,b的取值范围,再根据取值范围确定a,b的具体值,最后计算$\frac{a}{b}$。
首先,$a$为不超过$1\frac{1}{4}$的正整数,正整数包括0和正有理数,而$1\frac{1}{4}$大于1且小于2,所以a只能取1。
其次,$b$为$\frac{1}{2}$与$2\frac{1}{3}$之间的整数,$\frac{1}{2}$与$2\frac{1}{3}$之间的整数只有1和2,所以b可以取1或2。
当$a=1$,$b=1$时,$\frac{a}{b}=\frac{1}{1}=1$;
当$a=1$,$b=2$时,$\frac{a}{b}=\frac{1}{2}=0.5$。
【答案】:
$\frac{a}{b}=1或\frac{1}{2}$。
题目考查正负数的认识,以及正负数的取值范围,需要分别求出a,b的取值范围,再根据取值范围确定a,b的具体值,最后计算$\frac{a}{b}$。
首先,$a$为不超过$1\frac{1}{4}$的正整数,正整数包括0和正有理数,而$1\frac{1}{4}$大于1且小于2,所以a只能取1。
其次,$b$为$\frac{1}{2}$与$2\frac{1}{3}$之间的整数,$\frac{1}{2}$与$2\frac{1}{3}$之间的整数只有1和2,所以b可以取1或2。
当$a=1$,$b=1$时,$\frac{a}{b}=\frac{1}{1}=1$;
当$a=1$,$b=2$时,$\frac{a}{b}=\frac{1}{2}=0.5$。
【答案】:
$\frac{a}{b}=1或\frac{1}{2}$。
6. (教材 P14 练习 2 变式)
(1) 将下列各数填入相应的集合内:$2\frac{1}{2},$5,0,1.5,+2,-3;
(2) 说出这两个集合的重叠部分表示的是什么数的集合.
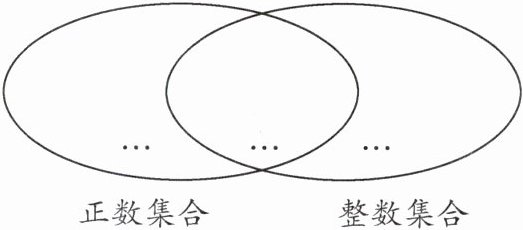
(1) 将下列各数填入相应的集合内:$2\frac{1}{2},$5,0,1.5,+2,-3;
(2) 说出这两个集合的重叠部分表示的是什么数的集合.

答案:【解析】:
本题主要考查了正数、负数和整数的定义以及集合的概念。
对于第一问,需要根据正数和整数的定义,将给定的数分类填入相应的集合。
正数是大于0的数,整数包括正整数、0和负整数。
对于第二问,需要找出正数集合和整数集合的重叠部分,即同时满足正数和整数条件的数,也就是正整数集合。
【答案】:
(1) 正数集合:$\{ 2\frac{1}{2}, 5, 1.5, +2 \}$;
整数集合:$\{ 5, 0, +2, -3 \}$;
(2) 这两个集合的重叠部分表示的是正整数集合,即$\{5,+2\}$。
本题主要考查了正数、负数和整数的定义以及集合的概念。
对于第一问,需要根据正数和整数的定义,将给定的数分类填入相应的集合。
正数是大于0的数,整数包括正整数、0和负整数。
对于第二问,需要找出正数集合和整数集合的重叠部分,即同时满足正数和整数条件的数,也就是正整数集合。
【答案】:
(1) 正数集合:$\{ 2\frac{1}{2}, 5, 1.5, +2 \}$;
整数集合:$\{ 5, 0, +2, -3 \}$;
(2) 这两个集合的重叠部分表示的是正整数集合,即$\{5,+2\}$。
7. (2024·四川凉山)给出下列各数:5,$-\frac{5}{7},$-3,0,-25.8,+2. 其中负数有 (
A.1 个
B.2 个
C.3 个
D.4 个
C
)A.1 个
B.2 个
C.3 个
D.4 个
答案:【解析】:
本题考察的是对正数与负数的识别能力。
首先,我们需要明确什么是负数。
负数是小于0的数,前面带有“-”号。
接下来,我们逐一判断给出的数是否为负数:
5:这是一个正数,不是负数。
$-\frac{5}{7}$:这是一个负数,因为它小于0且前面带有“-”号。
-3:这是一个负数,因为它小于0且前面带有“-”号。
0:0既不是正数也不是负数。
-25.8:这是一个负数,因为它小于0且前面带有“-”号。
+2:这是一个正数,前面的“+”号表示正,不是负数。
综上所述,负数有$-\frac{5}{7}$,-3,-25.8,共3个。
【答案】:
C
本题考察的是对正数与负数的识别能力。
首先,我们需要明确什么是负数。
负数是小于0的数,前面带有“-”号。
接下来,我们逐一判断给出的数是否为负数:
5:这是一个正数,不是负数。
$-\frac{5}{7}$:这是一个负数,因为它小于0且前面带有“-”号。
-3:这是一个负数,因为它小于0且前面带有“-”号。
0:0既不是正数也不是负数。
-25.8:这是一个负数,因为它小于0且前面带有“-”号。
+2:这是一个正数,前面的“+”号表示正,不是负数。
综上所述,负数有$-\frac{5}{7}$,-3,-25.8,共3个。
【答案】:
C
8. 下列说法正确的是 (
A.非负数一定是正数
B.既有最小的正整数,又有最小的有理数
C.a 一定是非负数
D.正整数和正分数统称为正有理数
D
)A.非负数一定是正数
B.既有最小的正整数,又有最小的有理数
C.a 一定是非负数
D.正整数和正分数统称为正有理数
答案:【解析】:
本题主要考察正数、负数、有理数、非负数的定义和性质。
A选项:非负数包括正数和0,因此非负数并不一定是正数,所以A选项错误。
B选项:正整数中最小的是1,这是明确的。但对于有理数,无论取多小的有理数,总可以找到一个更小的有理数(例如,该数再减去1),所以没有最小的有理数。因此B选项错误。
C选项:对于任意实数a,其平方$a^2$是非负的,但题目中说的是"a一定是非负数",这里并没有明确a是平方数或其他形式,直接说a一定是非负数是不准确的。例如,当a=-1时,a就是负数。所以C选项错误。但根据常规理解,此处可能题目意图是考察$\left | a \right | $(a的绝对值)或$a^{2}$(a的平方)等非负表示,然而题目中并未如此表述,因此按原题意判断C选项错误。
D选项:正有理数定义为大于0的有理数,这包括正整数和正分数。因此D选项正确。
【答案】:
D
本题主要考察正数、负数、有理数、非负数的定义和性质。
A选项:非负数包括正数和0,因此非负数并不一定是正数,所以A选项错误。
B选项:正整数中最小的是1,这是明确的。但对于有理数,无论取多小的有理数,总可以找到一个更小的有理数(例如,该数再减去1),所以没有最小的有理数。因此B选项错误。
C选项:对于任意实数a,其平方$a^2$是非负的,但题目中说的是"a一定是非负数",这里并没有明确a是平方数或其他形式,直接说a一定是非负数是不准确的。例如,当a=-1时,a就是负数。所以C选项错误。但根据常规理解,此处可能题目意图是考察$\left | a \right | $(a的绝对值)或$a^{2}$(a的平方)等非负表示,然而题目中并未如此表述,因此按原题意判断C选项错误。
D选项:正有理数定义为大于0的有理数,这包括正整数和正分数。因此D选项正确。
【答案】:
D
9. 我国古代用算筹计数,表示数的算筹有纵、横两种方式:
纵式: Ⅰ Ⅱ Ⅲ Ⅲ Ⅲ Ⅲ Ⅲ Ⅲ Ⅲ Ⅲ
横式: - = ≡ ≡ ≡ ⊥ ⊥ ⊥ ⊥
1 2 3 4 5 6 7 8 9
个位用纵式,十位用横式,百位再用纵式,千位再用横式,万位再用纵式,…,这样纵横依次交替. 如:614 用算筹表示出来是“T - Ⅲ”;若要表示负数,则可以在个位数上划上斜线. 如:-134 用算筹表示出来是“≡ Ⅲ”,则“⊥ T = メ”表示的数是______
纵式: Ⅰ Ⅱ Ⅲ Ⅲ Ⅲ Ⅲ Ⅲ Ⅲ Ⅲ Ⅲ
横式: - = ≡ ≡ ≡ ⊥ ⊥ ⊥ ⊥
1 2 3 4 5 6 7 8 9
个位用纵式,十位用横式,百位再用纵式,千位再用横式,万位再用纵式,…,这样纵横依次交替. 如:614 用算筹表示出来是“T - Ⅲ”;若要表示负数,则可以在个位数上划上斜线. 如:-134 用算筹表示出来是“≡ Ⅲ”,则“⊥ T = メ”表示的数是______
-8621
.答案:-8621