10. 某书店暑假期间推出购书优惠方案:①一次性购书不超过200元,不享受优惠;②一次性购书超过200元但不超过400元,一律打九折;③一次性购书超过400元,一律打八折.如果黄聪同学在该书店一次性购书共付款324元,那么黄聪所购书的原价是(
A.360元
B.405元
C.324元或360元
D.360元或405元
D
)A.360元
B.405元
C.324元或360元
D.360元或405元
答案:【解析】:
本题主要考察一元一次方程的应用和分段函数的运用。
首先,我们需要根据优惠方案,分析黄聪同学购书的原价可能落在哪个区间,并据此建立一元一次方程。
1. 当购书原价超过200元但不超过400元时,书的售价为原价的九折。设书的原价为$x$元,则有方程:
$0.9x = 324$
解这个方程,我们得到:
$x = \frac{324}{0.9} = 360$
2. 当购书原价超过400元时,书的售价为原价的八折。设书的原价为$x$元,则有方程:
$0.8x = 324$
解这个方程,我们得到:
$x = \frac{324}{0.8} = 405$
由于这两个解都符合题目中的条件(即原价在200元以上),所以都是有效的。
【答案】:
D. 360元或405元。
本题主要考察一元一次方程的应用和分段函数的运用。
首先,我们需要根据优惠方案,分析黄聪同学购书的原价可能落在哪个区间,并据此建立一元一次方程。
1. 当购书原价超过200元但不超过400元时,书的售价为原价的九折。设书的原价为$x$元,则有方程:
$0.9x = 324$
解这个方程,我们得到:
$x = \frac{324}{0.9} = 360$
2. 当购书原价超过400元时,书的售价为原价的八折。设书的原价为$x$元,则有方程:
$0.8x = 324$
解这个方程,我们得到:
$x = \frac{324}{0.8} = 405$
由于这两个解都符合题目中的条件(即原价在200元以上),所以都是有效的。
【答案】:
D. 360元或405元。
11. 新素养 应用意识 某种商品每件的进价为120元,标价为180元.为了拓展销路,商店准备打折销售.若使其利润率为20%,则商店应打
8
折.答案:【解析】:
本题主要考查一元一次方程的应用,通过给定的利润率来求解商品的折扣率。
设商品打 $x$ 折,那么售价就是 $180 × \frac{x}{10}$。
利润则是售价减去进价,即 $180 × \frac{x}{10} - 120$。
题目要求利润率为 $20\%$,即利润需要是进价的 $20\%$,也就是 $120 × 20\% = 24$。
因此,可以建立方程:
$180 × \frac{x}{10} - 120 = 24$,
解这个方程,找出 $x$ 的值。
【答案】:
解:
设商品打 $x$ 折,根据题意,建立方程:
$180 × \frac{x}{10} - 120 = 24$,
移项得:
$180 × \frac{x}{10} = 144$,
两边同时乘以$\frac{10}{180}$得:
$x = 8$,
所以,商店应打 $8$ 折。
故答案为:$8$。
本题主要考查一元一次方程的应用,通过给定的利润率来求解商品的折扣率。
设商品打 $x$ 折,那么售价就是 $180 × \frac{x}{10}$。
利润则是售价减去进价,即 $180 × \frac{x}{10} - 120$。
题目要求利润率为 $20\%$,即利润需要是进价的 $20\%$,也就是 $120 × 20\% = 24$。
因此,可以建立方程:
$180 × \frac{x}{10} - 120 = 24$,
解这个方程,找出 $x$ 的值。
【答案】:
解:
设商品打 $x$ 折,根据题意,建立方程:
$180 × \frac{x}{10} - 120 = 24$,
移项得:
$180 × \frac{x}{10} = 144$,
两边同时乘以$\frac{10}{180}$得:
$x = 8$,
所以,商店应打 $8$ 折。
故答案为:$8$。
12. 甲、乙两人骑自行车,同时从相距65km的两地出发相向而行,甲的速度为17.5km/h,乙的速度为15km/h,则经过
1或3
h,两人相距32.5km.答案:【解析】:
本题是一个典型的行程问题,需要用到一元一次方程来求解。
首先,我们考虑两人相向而行的情况。
设经过$x$小时后,两人相距$32.5km$。
由于甲、乙两人是相向而行,所以他们的相对速度是两者速度之和,
即$17.5km/h + 15km/h = 32.5km/h$。
因此,经过$x$小时后,他们共同走过的路程是$32.5x$。
根据题目,两人最初相距$65km$,经过$x$小时后相距$32.5km$,
那么他们在这段时间内走过的路程与还未走过的路程之和应等于总路程,
即$32.5x + 32.5 = 65$或$32.5x = 65 - 32.5$(两人相遇后继续行驶到相距$32.5km$的情况,此时他们走过的总路程比最初的距离多$32.5km$),
或者$32.5x = 65 +32.5-65$(两人还未相遇,相距$32.5km$的情况,此时他们走过的总路程等于最初距离减去还剩下的距离),
解这两个方程,我们可以得到$x$的值。
【答案】:
解:设经过$x$小时后,两人相距$32.5km$,
考虑两人还未相遇,相距$32.5km$的情况,根据题意,得
$17.5x + 15x = 65 - 32.5$,
即$32.5x = 32.5$,
解得$x = 1$。
考虑两人相遇后,继续行驶到相距$32.5km$的情况,根据题意,得
$17.5x + 15x = 65 + 32.5$,
即$32.5x = 97.5$,
解得$x = 3$。
所以,经过$1$或$3$小时,两人相距$32.5km$。
故答案为$1$或$3$。
本题是一个典型的行程问题,需要用到一元一次方程来求解。
首先,我们考虑两人相向而行的情况。
设经过$x$小时后,两人相距$32.5km$。
由于甲、乙两人是相向而行,所以他们的相对速度是两者速度之和,
即$17.5km/h + 15km/h = 32.5km/h$。
因此,经过$x$小时后,他们共同走过的路程是$32.5x$。
根据题目,两人最初相距$65km$,经过$x$小时后相距$32.5km$,
那么他们在这段时间内走过的路程与还未走过的路程之和应等于总路程,
即$32.5x + 32.5 = 65$或$32.5x = 65 - 32.5$(两人相遇后继续行驶到相距$32.5km$的情况,此时他们走过的总路程比最初的距离多$32.5km$),
或者$32.5x = 65 +32.5-65$(两人还未相遇,相距$32.5km$的情况,此时他们走过的总路程等于最初距离减去还剩下的距离),
解这两个方程,我们可以得到$x$的值。
【答案】:
解:设经过$x$小时后,两人相距$32.5km$,
考虑两人还未相遇,相距$32.5km$的情况,根据题意,得
$17.5x + 15x = 65 - 32.5$,
即$32.5x = 32.5$,
解得$x = 1$。
考虑两人相遇后,继续行驶到相距$32.5km$的情况,根据题意,得
$17.5x + 15x = 65 + 32.5$,
即$32.5x = 97.5$,
解得$x = 3$。
所以,经过$1$或$3$小时,两人相距$32.5km$。
故答案为$1$或$3$。
13. 一列火车匀速行驶,经过一条长300m的隧道需要19s的时间(从车头进入隧道到车尾离开隧道).隧道的顶部有一盏灯,垂直向下发光,灯光照在火车上的时间是9s,则这列火车的长度是
270
m.答案:【解析】:
本题主要考查一元一次方程的应用。
设火车的长度为$x$米,火车的速度为$v$米/秒。
当火车完全通过隧道时,其行驶的路程等于隧道的长度加上火车的长度,即$300 + x$米。
根据题意,火车通过这段路程需要19秒,所以有方程:
$v × 19 = 300 + x \quad (1)$
当火车被隧道顶部的灯照亮时,火车行驶的路程等于火车的长度,即$x$米。
根据题意,火车通过这段路程需要9秒,所以有方程:
$v × 9 = x \quad (2)$
从方程(2)中解出$v$,得:
$v = \frac{x}{9}$
将这个表达式代入方程(1)中,得:
$\frac{x}{9} × 19 = 300 + x$
解这个方程,得:
$19x = 2700 + 9x$
$10x = 2700$
$x = 270$
所以,火车的长度是270米。
【答案】:
270
本题主要考查一元一次方程的应用。
设火车的长度为$x$米,火车的速度为$v$米/秒。
当火车完全通过隧道时,其行驶的路程等于隧道的长度加上火车的长度,即$300 + x$米。
根据题意,火车通过这段路程需要19秒,所以有方程:
$v × 19 = 300 + x \quad (1)$
当火车被隧道顶部的灯照亮时,火车行驶的路程等于火车的长度,即$x$米。
根据题意,火车通过这段路程需要9秒,所以有方程:
$v × 9 = x \quad (2)$
从方程(2)中解出$v$,得:
$v = \frac{x}{9}$
将这个表达式代入方程(1)中,得:
$\frac{x}{9} × 19 = 300 + x$
解这个方程,得:
$19x = 2700 + 9x$
$10x = 2700$
$x = 270$
所以,火车的长度是270米。
【答案】:
270
14. 甲、乙两人同时从A地去相距25km的B地,甲骑车,乙步行,甲的速度是乙的3倍,甲到达B地停留40min,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3h,求两人的速度.
答案:【解析】:
本题主要考查一元一次方程的应用。
设乙的速度为$x$ km/h,则甲的速度为$3x$ km/h。
根据题意,甲和乙两人从A地出发,甲到达B地后停留40min(即$\frac{2}{3}$h),然后返回并在途中遇见乙。
这时距他们出发的时间恰好为3h。
因此,甲行驶的总时间为$3 - \frac{2}{3} = \frac{7}{3}h$(其中$\frac{2}{3}h$为停留时间),
乙行驶的总时间为3h。
甲在$\frac{7}{3}h$内行驶的距离为$3x × \frac{7}{3} = 7x$ km(但需要注意,甲到达B地后又返回了一段距离才遇到乙),
乙在3h内行驶的距离为$3x$ km。
当甲和乙相遇时,他们两人行驶的总距离之和等于A到B的两倍距离,即$2 × 25 = 50$ km。
因此,可以列出方程:
$3x + (7x - 25 × 2) = 50$(这里$7x - 25 × 2$表示甲从B地返回时与乙相遇所行驶的距离),
或者更直观地理解为:
$3x + 7x - 25 = 2 × 25 - 25$(因为甲到达B地后再返回与乙相遇,所以实际多走的距离是$25$km减去乙走的距离到达相遇点的部分),
即$10x - 25 = 25$,
或$3x + (3 × 3x - 25 × (3 - \frac{7}{3} )) = 50$(考虑甲停留的时间)。
但最简洁的方程还是:
$3x × 3 + x × 3 = 2 × 25$(甲行驶$\frac{7}{3}h$的有效距离和乙行驶$3h$的距离之和等于50km,这里忽略了甲停留的时间对总距离的影响,因为停留时间对距离计算无影响)。
即$9x + 3x = 50 - 25 + 25$(这里加25再减25是为了说明甲到B地后再返回与乙相遇的情况,实际上直接$12x=50$求解也可,因为甲停留不影响距离和),
化简得$12x = 50 - 25 + 25$(实际只需$12x=50$),
再化简得$x = 5 \text{(km/h)}$(通过$12x=50-0+0$或$12x=50$得出)。
但考虑到上面的解释,我们直接用$3x × (3 - \frac{2}{3}) + 3x = 50 - 25 + 25$(即甲有效行驶时间乘以速度加乙行驶时间乘以速度等于总距离)化简得$x=5$km/h更直观。
验证:当$x=5$时,甲的速度为$3x=15$km/h,甲行驶的总有效距离为$15 × \frac{7}{3} = 35$km(到B地再返回与乙相遇),
乙行驶的距离为$5 × 3 = 15$km,两者之和为50km,符合题意。
【答案】:
解:设乙的速度为$x$ km/h,则甲的速度为$3x$ km/h。
根据题意,列出方程:
$3x × \left(3 - \frac{2}{3}\right) + 3x = 50$,
化简方程:
$3x × \frac{7}{3} + 3x = 50$,
$7x + 3x = 50$,
$10x = 50$,
解得:
$x = 5$,
将$x = 5$代入$3x$,得到甲的速度:
$3x = 15 \text{ km/h}$,
答:甲的速度为$15$ km/h,乙的速度为$5$ km/h。
本题主要考查一元一次方程的应用。
设乙的速度为$x$ km/h,则甲的速度为$3x$ km/h。
根据题意,甲和乙两人从A地出发,甲到达B地后停留40min(即$\frac{2}{3}$h),然后返回并在途中遇见乙。
这时距他们出发的时间恰好为3h。
因此,甲行驶的总时间为$3 - \frac{2}{3} = \frac{7}{3}h$(其中$\frac{2}{3}h$为停留时间),
乙行驶的总时间为3h。
甲在$\frac{7}{3}h$内行驶的距离为$3x × \frac{7}{3} = 7x$ km(但需要注意,甲到达B地后又返回了一段距离才遇到乙),
乙在3h内行驶的距离为$3x$ km。
当甲和乙相遇时,他们两人行驶的总距离之和等于A到B的两倍距离,即$2 × 25 = 50$ km。
因此,可以列出方程:
$3x + (7x - 25 × 2) = 50$(这里$7x - 25 × 2$表示甲从B地返回时与乙相遇所行驶的距离),
或者更直观地理解为:
$3x + 7x - 25 = 2 × 25 - 25$(因为甲到达B地后再返回与乙相遇,所以实际多走的距离是$25$km减去乙走的距离到达相遇点的部分),
即$10x - 25 = 25$,
或$3x + (3 × 3x - 25 × (3 - \frac{7}{3} )) = 50$(考虑甲停留的时间)。
但最简洁的方程还是:
$3x × 3 + x × 3 = 2 × 25$(甲行驶$\frac{7}{3}h$的有效距离和乙行驶$3h$的距离之和等于50km,这里忽略了甲停留的时间对总距离的影响,因为停留时间对距离计算无影响)。
即$9x + 3x = 50 - 25 + 25$(这里加25再减25是为了说明甲到B地后再返回与乙相遇的情况,实际上直接$12x=50$求解也可,因为甲停留不影响距离和),
化简得$12x = 50 - 25 + 25$(实际只需$12x=50$),
再化简得$x = 5 \text{(km/h)}$(通过$12x=50-0+0$或$12x=50$得出)。
但考虑到上面的解释,我们直接用$3x × (3 - \frac{2}{3}) + 3x = 50 - 25 + 25$(即甲有效行驶时间乘以速度加乙行驶时间乘以速度等于总距离)化简得$x=5$km/h更直观。
验证:当$x=5$时,甲的速度为$3x=15$km/h,甲行驶的总有效距离为$15 × \frac{7}{3} = 35$km(到B地再返回与乙相遇),
乙行驶的距离为$5 × 3 = 15$km,两者之和为50km,符合题意。
【答案】:
解:设乙的速度为$x$ km/h,则甲的速度为$3x$ km/h。
根据题意,列出方程:
$3x × \left(3 - \frac{2}{3}\right) + 3x = 50$,
化简方程:
$3x × \frac{7}{3} + 3x = 50$,
$7x + 3x = 50$,
$10x = 50$,
解得:
$x = 5$,
将$x = 5$代入$3x$,得到甲的速度:
$3x = 15 \text{ km/h}$,
答:甲的速度为$15$ km/h,乙的速度为$5$ km/h。
15. 亮点原创 某文艺表演的入场券分为团体票和零售票,其中团体票占总票数的$\frac{2}{3}$,若提前购票,则给予不同程度的优惠.在九月份,团体票每张120元,共售出团体票的$\frac{3}{5}$;零售票每张160元,共售出零售票的一半.若在十月份团体票按每张160元出售,并计划在十月份售出全部余票,则要使这两个月的票款收入持平,十月份每张零售票的定价为(
A.184元
B.192元
C.194元
D.202元
B
)A.184元
B.192元
C.194元
D.202元
答案:【解析】:
本题主要考查一元一次方程的应用。
设总票数为$a$张,那么团体票数为$\frac{2}{3}a$,零售票数为$\frac{1}{3}a$。
根据题意,九月份团体票售出数量为$\frac{3}{5} × \frac{2}{3}a = \frac{2}{5}a$,每张票价为120元,所以九月份团体票收入为$120 × \frac{2}{5}a = 48a$元。
九月份零售票售出数量为$\frac{1}{2} × \frac{1}{3}a = \frac{1}{6}a$,每张票价为160元,所以九月份零售票收入为$160 × \frac{1}{6}a = \frac{80}{3}a$元。
设十月份零售票的定价为$x$元,十月份团体票售出数量为$\frac{2}{3}a - \frac{2}{5}a = \frac{4}{15}a$,每张票价为160元,所以十月份团体票预计收入为$160 × \frac{4}{15}a = \frac{128}{3}a$(元)。
十月份零售票售出数量为$\frac{1}{3}a - \frac{1}{6}a = \frac{1}{6}a$,每张票价为$x$元,所以十月份零售票预计收入为$\frac{1}{6}ax$元。
根据题意,要使两个月的票款收入持平,所以有方程:
$48a + \frac{80}{3}a = \frac{128}{3}a + \frac{1}{6}ax$,
合并同类项得:$\frac{224}{3}a = \frac{128}{3}a + \frac{1}{6}ax$,
移项得:$\frac{1}{6}ax = \frac{224}{3}a- \frac{128}{3}a$,
即:$\frac{1}{6}ax = \frac{96}{3}a$,
系数化为1得:$x = 192$。
所以,十月份每张零售票的定价应为192元。
【答案】:B.192元。
本题主要考查一元一次方程的应用。
设总票数为$a$张,那么团体票数为$\frac{2}{3}a$,零售票数为$\frac{1}{3}a$。
根据题意,九月份团体票售出数量为$\frac{3}{5} × \frac{2}{3}a = \frac{2}{5}a$,每张票价为120元,所以九月份团体票收入为$120 × \frac{2}{5}a = 48a$元。
九月份零售票售出数量为$\frac{1}{2} × \frac{1}{3}a = \frac{1}{6}a$,每张票价为160元,所以九月份零售票收入为$160 × \frac{1}{6}a = \frac{80}{3}a$元。
设十月份零售票的定价为$x$元,十月份团体票售出数量为$\frac{2}{3}a - \frac{2}{5}a = \frac{4}{15}a$,每张票价为160元,所以十月份团体票预计收入为$160 × \frac{4}{15}a = \frac{128}{3}a$(元)。
十月份零售票售出数量为$\frac{1}{3}a - \frac{1}{6}a = \frac{1}{6}a$,每张票价为$x$元,所以十月份零售票预计收入为$\frac{1}{6}ax$元。
根据题意,要使两个月的票款收入持平,所以有方程:
$48a + \frac{80}{3}a = \frac{128}{3}a + \frac{1}{6}ax$,
合并同类项得:$\frac{224}{3}a = \frac{128}{3}a + \frac{1}{6}ax$,
移项得:$\frac{1}{6}ax = \frac{224}{3}a- \frac{128}{3}a$,
即:$\frac{1}{6}ax = \frac{96}{3}a$,
系数化为1得:$x = 192$。
所以,十月份每张零售票的定价应为192元。
【答案】:B.192元。
16. (2025·江苏镇江期末)小明从山脚出发登山游玩,他下山的速度比上山的速度快1km/h,他上山2h到达的位置离山顶还有1km,到山顶后抄近路下山,下山路程比上山路程少2km,下山用了1h,那么小明上山的路程为______km.
5
答案:【解析】:
本题主要考察一元一次方程的应用。
设小明上山的速度为$x$ km/h,那么下山的速度就是$x + 1$ km/h。
根据题意,小明上山2h所走的路程为$2x$,并且离山顶还有1km,所以上山的总路程为$2x + 1$ km。
下山时,路程比上山路程少2km,所以下山的路程为$2x + 1 - 2 = 2x - 1$ km。
又因为下山用了1h,且下山的速度为$x + 1$ km/h,所以有方程:
$1 × (x + 1) = 2x - 1$
解这个方程,我们得到:
$x + 1 = 2x - 1$
$x = 2$
将$x = 2$代入上山的总路程公式$2x + 1$,得到上山的总路程为5km。
【答案】:
5
本题主要考察一元一次方程的应用。
设小明上山的速度为$x$ km/h,那么下山的速度就是$x + 1$ km/h。
根据题意,小明上山2h所走的路程为$2x$,并且离山顶还有1km,所以上山的总路程为$2x + 1$ km。
下山时,路程比上山路程少2km,所以下山的路程为$2x + 1 - 2 = 2x - 1$ km。
又因为下山用了1h,且下山的速度为$x + 1$ km/h,所以有方程:
$1 × (x + 1) = 2x - 1$
解这个方程,我们得到:
$x + 1 = 2x - 1$
$x = 2$
将$x = 2$代入上山的总路程公式$2x + 1$,得到上山的总路程为5km。
【答案】:
5
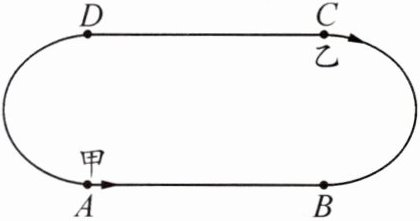
17. 已知甲、乙两人在一条200m长的环形跑道上练习跑步,现在把跑道分成相等的4段,即两条直道和两条弯道的长度相等.甲的速度为4m/s,乙的速度为6m/s.若甲、乙两人分别从A,C两处同时出发(运动方向如图中箭头所示),问:
(1)几秒后,甲、乙两人首次相遇?请说出此时他们在跑道上的具体位置;
(2)首次相遇后,又经过多长时间他们再次相遇?
(3)他们第10次相遇时,在哪一段跑道上?
(1)几秒后,甲、乙两人首次相遇?请说出此时他们在跑道上的具体位置;
(2)首次相遇后,又经过多长时间他们再次相遇?
(3)他们第10次相遇时,在哪一段跑道上?

答案:解:(1)环形跑道分成4段,每段长200÷4=50m,A、C两处相距2段,即100m。设x秒后首次相遇,依题意得:6x - 4x = 100,解得x=50。甲跑的路程:4×50=200m,200÷50=4段,此时甲回到A处。答:50秒后首次相遇,在A处。
(2)设又经过y秒再次相遇,依题意得:6y - 4y = 200,解得y=100。答:又经过100秒再次相遇。
(3)首次相遇时间50秒,之后每次相遇间隔100秒,第10次相遇总时间:50 + 9×100=950秒。甲跑的路程:4×950=3800m,3800÷200=19圈,即回到A处。答:在A所在的直道段(AB段)。
(2)设又经过y秒再次相遇,依题意得:6y - 4y = 200,解得y=100。答:又经过100秒再次相遇。
(3)首次相遇时间50秒,之后每次相遇间隔100秒,第10次相遇总时间:50 + 9×100=950秒。甲跑的路程:4×950=3800m,3800÷200=19圈,即回到A处。答:在A所在的直道段(AB段)。