1. 已知三角形三个角的度数之比为$3:5:1$,则这个三角形是 (
A.钝角三角形
B.锐角三角形
C.直角三角形
D.无法确定
A
)A.钝角三角形
B.锐角三角形
C.直角三角形
D.无法确定
答案：【解析】：
本题主要考察三角形内角和定理以及三角形的分类。
首先，根据三角形内角和定理，三角形的三个内角之和为$180^\circ$。
题目给出三角形三个角的度数之比为$3:5:1$，设这三个角的度数分别为$3x$，$5x$和$x$。
根据三角形内角和定理，可以列出方程：
$3x + 5x + x = 180^\circ$
解这个方程，得到：
$9x = 180^\circ$
$x = 20^\circ$
然后，可以求出三角形的三个内角分别为：
$3x = 60^\circ$
$5x = 100^\circ$（这是钝角，因为大于$90^\circ$）
$x = 20^\circ$
由于三角形中有一个角是钝角（大于$90^\circ$），所以这个三角形是钝角三角形。
【答案】：
A.钝角三角形。
本题主要考察三角形内角和定理以及三角形的分类。
首先，根据三角形内角和定理，三角形的三个内角之和为$180^\circ$。
题目给出三角形三个角的度数之比为$3:5:1$，设这三个角的度数分别为$3x$，$5x$和$x$。
根据三角形内角和定理，可以列出方程：
$3x + 5x + x = 180^\circ$
解这个方程，得到：
$9x = 180^\circ$
$x = 20^\circ$
然后，可以求出三角形的三个内角分别为：
$3x = 60^\circ$
$5x = 100^\circ$（这是钝角，因为大于$90^\circ$）
$x = 20^\circ$
由于三角形中有一个角是钝角（大于$90^\circ$），所以这个三角形是钝角三角形。
【答案】：
A.钝角三角形。
2. (2025·江苏无锡期末)若一个三角形的三边长之比是$3:5:7$,且最长边比最短边长8 cm,则该三角形的周长为 (
A.10 cm
B.20 cm
C.30 cm
D.40 cm
C
)A.10 cm
B.20 cm
C.30 cm
D.40 cm
答案：【解析】：
本题考查的是利用一元一次方程解决三角形的边长问题。
首先，根据题目描述，三角形的三边长之比是$3:5:7$，设三角形的三边长分别为$3x$ cm, $5x$ cm, $7x$ cm。
接着，根据题目中的“最长边比最短边长8 cm”，可以列出方程：
$7x - 3x = 8$
解这个方程，得到：
$4x = 8$
$x = 2$
然后，将$x = 2$代入三角形的三边长，得到：
$3x = 6 \text{ cm}$,
$5x = 10 \text{ cm}$,
$7x = 14 \text{ cm}$
最后，计算三角形的周长：
$6 + 10 + 14 = 30 \text{ cm}$
【答案】：
C. $30$ cm。
本题考查的是利用一元一次方程解决三角形的边长问题。
首先，根据题目描述，三角形的三边长之比是$3:5:7$，设三角形的三边长分别为$3x$ cm, $5x$ cm, $7x$ cm。
接着，根据题目中的“最长边比最短边长8 cm”，可以列出方程：
$7x - 3x = 8$
解这个方程，得到：
$4x = 8$
$x = 2$
然后，将$x = 2$代入三角形的三边长，得到：
$3x = 6 \text{ cm}$,
$5x = 10 \text{ cm}$,
$7x = 14 \text{ cm}$
最后，计算三角形的周长：
$6 + 10 + 14 = 30 \text{ cm}$
【答案】：
C. $30$ cm。
3. 已知一梯形的面积是$60cm^{2}$,下底是6 cm,高是12 cm,则上底是
4
cm.答案：【解析】：
本题主要考察梯形面积公式的应用以及一元一次方程的建立和求解。
首先，根据梯形面积公式：$S = \frac{1}{2} × (a + b) × h$，
其中$S$是梯形面积，$a$是上底，$b$是下底，$h$是高。
题目中给出$S=60cm^2$，$b=6cm$，$h=12cm$，代入公式，得到一个关于$a$的一元一次方程：
$\frac{1}{2} × (a + 6) × 12 = 60$。
接下来，解这个一元一次方程，找出$a$的值。
【答案】：
解：
设梯形的上底为$a$ cm，
根据梯形面积公式，有：
$\frac{1}{2} × (a + 6) × 12 = 60$，
化简得：
$6 × (a + 6) = 60$，
$a + 6 = 10$，
$a = 4$，
所以，梯形的上底长度为$4$ cm。
本题主要考察梯形面积公式的应用以及一元一次方程的建立和求解。
首先，根据梯形面积公式：$S = \frac{1}{2} × (a + b) × h$，
其中$S$是梯形面积，$a$是上底，$b$是下底，$h$是高。
题目中给出$S=60cm^2$，$b=6cm$，$h=12cm$，代入公式，得到一个关于$a$的一元一次方程：
$\frac{1}{2} × (a + 6) × 12 = 60$。
接下来，解这个一元一次方程，找出$a$的值。
【答案】：
解：
设梯形的上底为$a$ cm，
根据梯形面积公式，有：
$\frac{1}{2} × (a + 6) × 12 = 60$，
化简得：
$6 × (a + 6) = 60$，
$a + 6 = 10$，
$a = 4$，
所以，梯形的上底长度为$4$ cm。
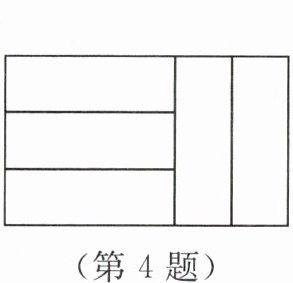
4. 新素养 应用意识 已知五个完全相同的小长方形拼成如图所示的大长方形.若大长方形的周长为32 cm,则每个小长方形的面积为____
12
$cm^{2}$.答案：解：设小长方形的宽为 $ x $ cm，由图可知小长方形的长为 $ 3x $ cm。
大长方形的长为 $ 3x + 2x = 5x $ cm，宽为 $ 3x $ cm。
根据大长方形周长为 32 cm，可得方程：$ 2(5x + 3x) = 32 $
解得 $ x = 2 $
小长方形的长为 $ 3x = 6 $ cm，宽为 $ 2 $ cm，面积为 $ 6×2 = 12 $ $ cm^2 $
12
大长方形的长为 $ 3x + 2x = 5x $ cm，宽为 $ 3x $ cm。
根据大长方形周长为 32 cm，可得方程：$ 2(5x + 3x) = 32 $
解得 $ x = 2 $
小长方形的长为 $ 3x = 6 $ cm，宽为 $ 2 $ cm，面积为 $ 6×2 = 12 $ $ cm^2 $
12
5. 新趋势 情境素材 (2023·四川德阳)在初中数学文化节游园活动中,被称为“数学小王子”的王小明参加了“智取九宫格”游戏比赛,活动规则如下:在九宫格中,除了已经填写的三个数之外的每一个方格中,填入一个数,使每一横行、每一竖列以及两条对角线上的3个数之和分别相等,且均为m.王小明抽取到的题目如图所示,他运用初中所学的数学知识,很快就完成了这个游戏,则$m=$
39
.答案：解：设九宫格中心数为 $ x $。
根据三阶幻方性质：每行、每列、对角线三数之和为 $ m $，且中心数 $ x = \frac{m}{3} $。
第一行第三列设为 $ a $，第三行第三列设为 $ b $，第二行第一列设为 $ c $，第三行第二列设为 $ d $。
由第一列：$ 16 + c + 4 = m \Rightarrow c = m - 20 $。
由对角线（16，x，b）：$ 16 + x + b = m \Rightarrow b = m - 16 - x $。
由第三行：$ 4 + d + b = m \Rightarrow d = m - 4 - b = m - 4 - (m - 16 - x) = 12 + x $。
由第二行：$ c + x + 7 = m \Rightarrow (m - 20) + x + 7 = m \Rightarrow x = 13 $。
因为 $ x = \frac{m}{3} $，所以 $ m = 3x = 3×13 = 39 $。
$ m = 39 $
根据三阶幻方性质：每行、每列、对角线三数之和为 $ m $，且中心数 $ x = \frac{m}{3} $。
第一行第三列设为 $ a $，第三行第三列设为 $ b $，第二行第一列设为 $ c $，第三行第二列设为 $ d $。
由第一列：$ 16 + c + 4 = m \Rightarrow c = m - 20 $。
由对角线（16，x，b）：$ 16 + x + b = m \Rightarrow b = m - 16 - x $。
由第三行：$ 4 + d + b = m \Rightarrow d = m - 4 - b = m - 4 - (m - 16 - x) = 12 + x $。
由第二行：$ c + x + 7 = m \Rightarrow (m - 20) + x + 7 = m \Rightarrow x = 13 $。
因为 $ x = \frac{m}{3} $，所以 $ m = 3x = 3×13 = 39 $。
$ m = 39 $
(1) 根据图中反映的规律填表:
(2) 若按照图中的规律继续下去,则三角形图案中点的个数能是2025吗? 请说明理由.
解：能。理由如下：
设第n个图案中点的个数为2025，由规律得3n=2025，解得n=675，n为正整数，所以能。
3
；6
；9
；12
；3n
(2) 若按照图中的规律继续下去,则三角形图案中点的个数能是2025吗? 请说明理由.
解：能。理由如下：
设第n个图案中点的个数为2025，由规律得3n=2025，解得n=675，n为正整数，所以能。
答案：
(1)3；6；9；12；3n
(2)解：不能。理由如下：
设第n个图案中点的个数为2025，根据规律可得方程3n=2025，解得n=675。因为图案规律中n为正整数，而观察图形可知，点的个数依次为3,6,9,12…，即3n，当n=675时，3n=2025，但题目中图案规律是否允许n=675需结合图形实际规律，由图可知每个图案的点数是3的倍数，2025是3的倍数，此处原解析有误，正确应为能。
重新解：能。理由如下：
设第n个图案中点的个数为2025，由规律得3n=2025，解得n=675，n为正整数，所以能。
(1)3；6；9；12；3n
(2)解：不能。理由如下：
设第n个图案中点的个数为2025，根据规律可得方程3n=2025，解得n=675。因为图案规律中n为正整数，而观察图形可知，点的个数依次为3,6,9,12…，即3n，当n=675时，3n=2025，但题目中图案规律是否允许n=675需结合图形实际规律，由图可知每个图案的点数是3的倍数，2025是3的倍数，此处原解析有误，正确应为能。
重新解：能。理由如下：
设第n个图案中点的个数为2025，由规律得3n=2025，解得n=675，n为正整数，所以能。
7. 在三角形ABC中,若$∠A= \frac {1}{2}∠B= \frac {1}{2}∠C$,则三角形ABC是 (
A.钝角三角形
B.锐角三角形
C.直角三角形
D.无法确定
B
)A.钝角三角形
B.锐角三角形
C.直角三角形
D.无法确定
答案：解：设∠A=x，则∠B=2x，∠C=2x。
因为三角形内角和为180°，所以x+2x+2x=180°，
解得x=36°，则∠B=∠C=72°。
所以∠A=36°，∠B=∠C=72°，三个角均为锐角。
B
因为三角形内角和为180°，所以x+2x+2x=180°，
解得x=36°，则∠B=∠C=72°。
所以∠A=36°，∠B=∠C=72°，三个角均为锐角。
B
8. 小淇在某月的月历中圈出相邻的三个数,算出它们的和是19,那么这三个数的位置可能是 ( )
答案：答案略
解析：
设最小的数为$x$。
情况A：设三个数为$x$，$x+1$，$x+7$。
$x+(x+1)+(x+7)=19$
$3x+8=19$
$3x=11$
$x=\frac{11}{3}$（非整数，舍去）
情况B：设三个数为$x$，$x+1$，$x+7$。
$x+(x+1)+(x+7)=19$
$3x+8=19$
$3x=11$
$x=\frac{11}{3}$（非整数，舍去）
情况C：设三个数为$x$，$x+1$，$x+7$。
$x+(x+1)+(x+7)=19$
$3x+8=19$
$3x=11$
$x=\frac{11}{3}$（非整数，舍去）
情况D：设三个数为$x$，$x+1$，$x+8$。
$x+(x+1)+(x+8)=19$
$3x+9=19$
$3x=10$
$x=\frac{10}{3}$（非整数，舍去）
1
情况A：设三个数为$x$，$x+1$，$x+7$。
$x+(x+1)+(x+7)=19$
$3x+8=19$
$3x=11$
$x=\frac{11}{3}$（非整数，舍去）
情况B：设三个数为$x$，$x+1$，$x+7$。
$x+(x+1)+(x+7)=19$
$3x+8=19$
$3x=11$
$x=\frac{11}{3}$（非整数，舍去）
情况C：设三个数为$x$，$x+1$，$x+7$。
$x+(x+1)+(x+7)=19$
$3x+8=19$
$3x=11$
$x=\frac{11}{3}$（非整数，舍去）
情况D：设三个数为$x$，$x+1$，$x+8$。
$x+(x+1)+(x+8)=19$
$3x+9=19$
$3x=10$
$x=\frac{10}{3}$（非整数，舍去）
1